Тема Треугольники с фиксированными углами

Треугольник с углом 60 градусов

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела треугольники с фиксированными углами

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#79116

Точка $N$ — середина стороны $BC$ треугольника $ABC,$ в котором $∠ACB =60∘.$ Точка $M$ на стороне $AC$ такова, что $AM = BN.$ Точка $K$ — середина отрезка $BM.$ Докажите, что $AK = KC.$

Показать доказательство

Отметим на $AC$ точку $T$ такую, что $TC = CN =T N.$

$PIC$

Тогда $BT C$ прямоугольный треугольник. Значит, перпендикуляр из $K$ на $MT$ падает в середину по теореме Фалеса, следовательно, $K$ лежит на серединном перпендикуляре $MT.$ А так как $AM = TC,$ то $K$ лежит и на серединном перпендикуляре $AC.$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#97382

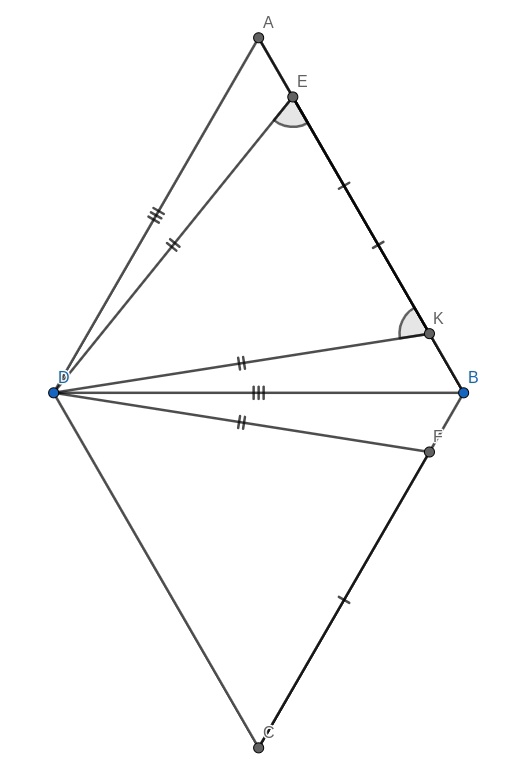
Точки $E$ и $F$ лежат на сторонах соответственно $AB$ и $BC$ ромба $ABCD,$ причём $AE = 5BE,$ $BF = 5CF.$ Известно, что треугольник $DEF$ — равносторонний. Найдите угол $BAD.$

Подсказки к задаче

Подсказка 1

Отметьте точку K на стороне AB такую, что AK = BE. Теперь попробуйте найти равные треугольники с общей вершиной в точке D.

Подсказка 2

Попробуйте теперь доказать, что углы AKD и BED равны, и найти с ними пару равных треугольников.

Подсказка 3

Из равенства треугольников AKD и BED следует равенство отрезков AD и BD. Осталось вспомнить, что ABCD является ромбом.

Показать ответ и решение

На стороне $AB$ отложим отрезок $AK =CF = BE.$ Из равенства треугольников $AKD$ и $CF D$ (по двум сторонам и углу между ними) следует, что $DK = DF = ED.$ Углы при основании $KE$ равнобедренного треугольника $DKE$ равны, поэтому равны и смежные им углы $AKD$ и $BED,$ и треугольники $AKD$ и $BED$ равны по двум сторонам и углу между ними. Значит, $BD = AD =AB,$ то есть треугольник $ABD$ равносторонний. Следовательно, $∘ ∠BAD = 60 .$

$PIC$

Ответ:

$∠BAD =60∘$

Ошибка.
Попробуйте повторить позже

Задача 3#58010

В треугольнике $ABC$ медиана, проведённая из вершины $A,$ в четыре раза меньше стороны $AB$ и образует с этой стороной угол $60∘.$ Найдите угол $∠BAC.$

Показать ответ и решение

Обозначим медиану из вершины $A$ через $AM.$

Первое решение.

Опустим перпендикуляр $BH$ на прямую $AM.$ Тогда в прямоугольном треугольнике $ABH$ катет $AH$ равен половине гипотенузы $AB,$ так как лежит напротив угла в $30$ градусов. А ещё по условию $1 AM = 4AB.$ Тогда $AB- AB- AB- MH =AH − AM = 2 − 4 = 4 =AM.$ Получили, что в четырёхугольнике $ABHC$ диагонали точкой пересечения $M$ делятся пополам, а значит, это параллелограмм, так что $∘ ∠CAH =∠AHB = 90 .$ В итоге $∘ ∘ ∘ ∠ABC =60 + 90 =150 .$

$PIC$

Второе решение.

Отметим ещё середину $AB$ — как $D,$ а середину $AD$ — как $E.$ Тогда $AE = 14AB,$ а ещё по условию $AM = 14AB.$ Так что треугольник $AME$ — равносторонний ( $AE =AM$ ) с углом при вершине $A$ в $60∘,$ значит, он равносторонний.

Тогда $∠DEM = 120∘,$ как смежный с углом в $60∘.$ Далее, $EM =AE = DE,$ поэтому треугольник $AMD$ — прямоугольный, и $∠EDM = 30∘.$ Смежный с ним $∠BDM = 150∘.$ С другой стороны, этот же угол равен $∠BAC,$ так как $DM$ — средняя линия треугольника $ABC$ — параллельна $AC.$

$PIC$

Третье решение.

Не будем думать и просто посчитаем:

1) по теореме косинусов для треугольника $AMB$

BM2 =AM2 + (4AM)2− 2⋅AM ⋅(4AM )⋅cos60∘ = 13AM2

2) по формуле медианы (при удвоение медианы получается параллелограмм, у которого сумма квадратов диагоналей равна сумме квадратов всех сторон)

(2AM )2 +BC2 = 2(AC2 +AB2 ) =⇒ 4AM2 + 4⋅13AM2 = 2AC2 +32AM2

12AM2 = AC2

3) по теореме косинусов для треугольника $ABC$

(2BM )2 = (4AM )2+ AC2− 2⋅(4AM )⋅AC cos∠BAC

2 2 2 √-- 2 4⋅13AM = 16AM + 12AM − 8⋅ 12⋅AM cos∠BAC

-24- √3- ∘ cos∠BAC = −8√12-= − 2 =⇒ ∠BAC =150

Ответ:

$150∘$

Ошибка.
Попробуйте повторить позже

Задача 4#67145

Равносторонние треугольники $ABC$ и $PQR$ расположены так, что вершина $C$ лежит на стороне $PQ$ , а вершина $R$ — на стороне $AB$ . Докажите, что $AP||BQ$ .

Подсказки к задаче

Подсказка 1

Хм, здесь есть много равных углов. Это намекает на то, что стоит поискать вписанные четырёхугольники!

Подсказка 2

Конечно, тут есть два вписанных четырёхугольника, имеющих общую сторону CR. Как же воспользоваться их вписанностью?

Подсказка 3

Верно, используем факт, что противоположные углы в сумме дают 180 градусов, надо просто перекинуть уголки, чтобы получить нужную сумму односторонних углов для искомых прямых!

Показать ответ и решение

Проведем $PA,CR,QB,$ рассмотрим четырехугольники $APCR$ и $CQBR$ .

$PIC$

∠CPR = ∠CAR = 60∘ ⇒ APCR —вписанный ∠CQR = ∠CBR = 60∘ ⇒ CQBR —вписанный

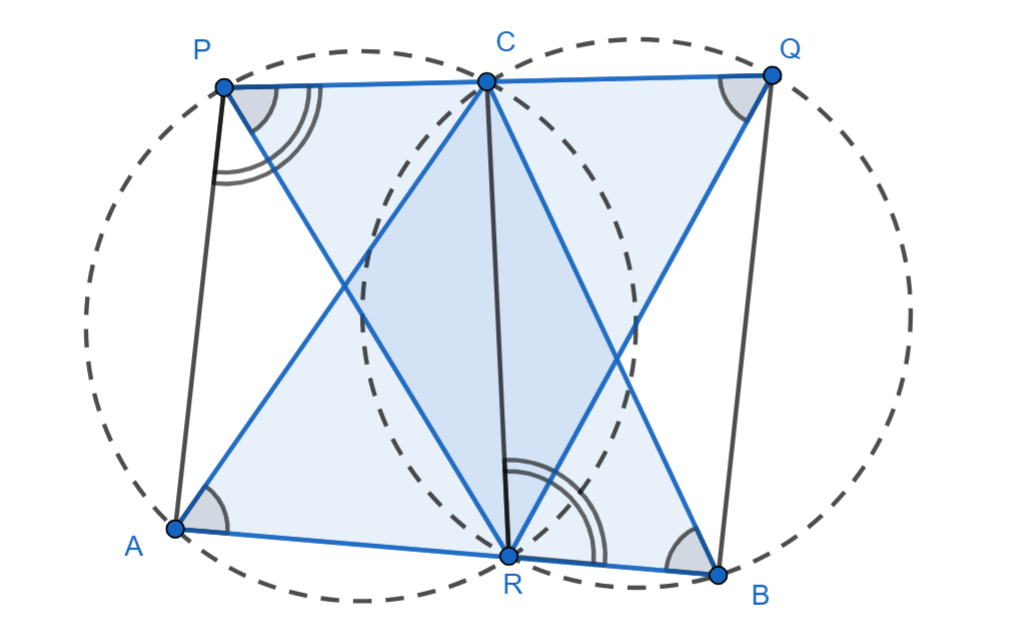
Поэтому

∠APC = ∠APQ = 180∘− ∠ARC = ∠CRB = 180∘− ∠CQB = 180∘− ∠P QB

Следовательно, $AP||BQ.$

Ответ:

что и требовалось доказать

Ошибка.
Попробуйте повторить позже

Задача 5#74129

Неравнобедренный треугольник $ABC,$ в котором $∠ACB =60∘,$ вписан в окружность $Ω.$ На биссектрисе угла $BAC$ выбрана точка $A′,$ а на биссектрисе угла $ABC$ — точка $′ B$ так, что $′ AB ∥ BC$ и $′ BA ∥AC.$ Прямая $′ ′ AB$ пересекает $Ω$ в точках $D$ и $E.$ Докажите, что треугольник $CDE$ равнобедренный.

Показать доказательство

Так как $∠AB′B =∠CBB ′ = ∠ABB ′,$ то $AB′ = AB.$ Аналогично $AB =A ′B.$ Обозначим $∠A = 2α,∠B = 2β.$ Пусть $α> β.$ Обозначим через $′ E$ середину дуги $ACB$ окружности $Ω.$ Тогда треугольник $′ ABE$ равносторонний( $′ ∘ ∠AE B = ∠C =60$ ). Поэтому точка $A$ — центр описанной окружности треугольника $′ ′ BE B .$ Следовательно:

′ ′ ′ ′ ∘ ∠E AB = 2∠E BB =120 − 2β

′ ′ ∘ ′ ′ ∘ ∠AE B =90 − 1∕2∠E AB =30 + β

Аналогично $∠BE ′A′ = 30∘+α,$ откуда

∠B ′E′A+ ∠AE ′B +∠BE ′A′ = (30∘+ β)+60∘+ (30∘+ α)=180∘

Итак, точка $E′$ лежит на прямой $A′B′,$ будем считать, что она совпадает с $E.$ Пусть $T$ — середина меньшей дуги $EC$ окружности $Ω.$ Заметим, что

∠AET =∠ABT =1∕2(∠ABE +∠B )=30∘+ β = ∠AEB ′

Значит, точка $T$ также лежит на прямой $A′B′,$ и треугольник $CDE$ совпадает с треугольником $CET.$ Этот треугольник равнобедренный, поскольку $ET = EC.$

$PIC$

Ошибка.
Попробуйте повторить позже

Задача 6#97702

В треугольнике $ABC$ с углом $∠C =60∘$ сторона $BC$ больше стороны $AC.$ Точка $D ⁄= A$ на отрезке $AC$ такова, что $AB = BD,$ а точка $E ⁄=B$ на прямой $BC$ такова, что $AB =AE.$ Найдите величину угла $∠DEC$ (в градусах).

Показать ответ и решение

Поскольку $∠C =60∘,$ то сторона $AB$ — средняя по величине: по условию $AC < BC,$ значит $∠CBA < ∠CAB.$ Поскольку сумма углов в треугольнике равна $∘ 180 ,$ угол $∠C$ наименьшим быть не может: иначе сумма углов треугольника выходит больше или меньше $∘ 180 .$ Таким образом, имеем $AC < AB <BC.$ Тогда, поскольку $AE =AB,$ то точка $E$ обязательно лежит вне треугольника.

Обозначим $∠CBA =β,$ $∠CAB =α.$

$PIC$

Из суммы углов треугольника $△ABC$ имеем $α+ β = 120∘.$ Запишем теорему синусов для $△BCD :$

-BD-- =---CD--- sin60∘ sin∠CBD

По теореме синусов для $△CAE :$

-AE--- --CE---- sin120∘ = sin∠CAE

Поскольку $AE = AB =BD$ и $∘ ∘ sin 60 = sin120 ,$ получаем

CE CD sin∠CAE--= sin∠CBD--

Докажем, что $∠CAE = ∠CBD.$

Треугольник $ABE$ равнобедренный $∠AEB = ∠EBA = β.$ Также имеем $∠DAB =∠ADB = α,$ так как $ADB$ равнобедренный. Так как $∠ADB = α,$ то $∠CDB = 180∘ − α.$ Из суммы углов треугольника $CDB$ получаем $∠CBD =α − 60∘.$ Из суммы углов треугольника $CEA$ получаем

∠EAC = 180∘− ∠ECA − ∠CEA = 60∘− β.

$60∘− β = α − 60∘$ эквивалентно $α+ β = 120∘,$ а это равенство мы уже проверили. Тогда $∠CAE = ∠CBD,$ поэтому $CE = CD.$

Так как

∠EDB = ∠EDC +∠CDB =∠EDC +180∘− α,

то по сумме углов в $△EDB :$

∠CED + ∠CDE + 180∘− α+ α− 60∘ = 180∘,

откуда

∘ 2∠CED =60

∘ ∠CED = 30

Ответ: 30

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#38693

В равнобедренном треугольнике $ABC$ ( $AB =BC$ ) радиус описанной окружности равен стороне $AC$ . На стороне $AC$ построили квадрат $ACKL$ так, что $KL$ пересекает боковые стороны треугольника. Найдите угол $BLK.$

Подсказки к задаче

Подсказка 1

Трудно работать с окружностью, когда мы не знаем, где ее центр. Тем более, удобно отметить его, если треугольник, который вписан в эту окружность - равнобедренный. Давайте отметим центр описанной окружности O и поймем что-то про эту точку и отрезки, которые она соединяет.

Подсказка 2

Верно, BO = OA, при этом OA = AC, и при этом AC = CL. Значит, BO = LA. Что тогда можно сказать про четырехугольник ALBO? Мы ведь еще никак не связали с картинкой BO(ну почти никак).

Подсказка 3

Можно сказать, что BO перпендикулярно AC, а значит, параллельно AL. Тогда, выходит, что ALBO - параллелограмм. Но ведь тогда AO || LB. Что тогда можно сказать, зная это и что AOC - равносторонний?

Показать ответ и решение

Обозначим центр описанной окружности треугольника за $O$ . Тогда $OB = OA = OC =AC$ , а также $AK = AC = CK = KL$ . Так как треугольник $ABC$ равнобедренный, то $BO$ — является высотой, а значит, $OB ⊥ AC$ . А также $KC ⊥ AC$ . Таким образом, $OB =CK$ и $OB ∥ CK$ , а значит, $BOCK$ — параллелограмм, откуда $BK = OC = AC$ .

Аналогично получаем, что $BL = AC$ , а значит, $BK =BL = KL$ и треугольник $BKL$ — равносторонний, а значит, $∘ ∠KBL =60$ .

$PIC$

Ответ: 60

Ошибка.
Попробуйте повторить позже

Задача 8#72242

В остроугольном неравнобедренном треугольнике $ABC$ проведены высоты $AA 1$ и $CC , 1$ и отмечены точки $K,$ $L$ и $M$ — середины сторон $AB,$ $BC$ и $CA$ соответственно. Докажите, что если $∠C1MA1 =∠ABC,$ то $C1K = A1L.$

Источники: Муницип - 2022, Орловская область, 10.3

Подсказки к задаче

Подсказка 1

Давайте для начала подумаем, что нам дает равенство уголочков ∠ABC и ∠A₁MC₁. Мы знаем, что сумма уголков ∠C₁MA+∠C₁MA₁+∠A₁MC=180°. Как нам выразить ∠C₁MA и ∠A₁MC через углы треугольника ∠ABC?

Подсказка 2

Т.к. △AMC₁ и △CMA₁- равнобедренные, то ∠AMC₁=180°-2∠BAC, ∠CMA₁=180°-2∠BCA ⇒ ∠ABC=2(180°-∠ABC)-180° ⇒ ∠ABC=60°. Тогда очень интересным выглядит треугольник △BC₁C. Что можно сказать про сторону BC₁?

Подсказка 3

Верно, она равна BC/2. Но мы знаем, что BL=BC/2 ⇒ BC₁=BL. Из аналогичных рассуждений можно получить, что BK=BA₁. Как тогда завершить решение?

Подсказка 4

Посмотрите на равенство BC₁-BK=BL-BA₁!

Показать доказательство

$PIC$

Давайте сначала узнаем, для чего же нам дали равенство углов. Пусть $∠ABC = β,∠ACB = γ,∠BAC =α.$ Тогда можем выразить угол $C1MA1$ через два других угла треугольника. Понятно, что $AM = CM =C1M = A1M.$ Тогда

∠AMC1 =180∘− 2α ∠CMA1 = 180∘− 2β

∠C1MA1 = β = 180∘− (180∘− 2α)− (180∘ − 2β)= 2(α +β)− 180∘

Но мы знаем, что $∘ α +β +γ =180 .$ Тогда

β =2(180∘− β)− 180∘

∘ β = 60

Отлично! Значит, на самом деле нам дали треугольник с углом $60∘.$ Но тогда $KL = C1A1 = AC2 ,$ так как $KL$ — это средняя линия треугольника, а $△A BC 1 1$ подобен исходному с коэффициентом $cos60∘,$ откуда и получаем равенство. Теперь видим, что если докажем равенство треугольников $KC1L$ и $A1C1L,$ то мы победим! Одна пара сторон у них равные, а $C1L$ общая сторона. Давайте найдём угол между ними. Будем использовать знания о том, что $ACA1C1$ вписанный, $KL$ параллельно $AC$ и из прямоугольного треугольника $BC1 = BL= C1L.$ Тогда

∠KLC1 = ∠C1LB − ∠KLB = ∠LC1B− ∠A1C1B = ∠LC1A1

Значит, треугольники $KC1L$ и $A1C1L$ равны по двум сторонам и углу между ними. Тогда и $KC1 = A1L.$ Победа!

Ошибка.
Попробуйте повторить позже

Задача 9#91921

На сторонах $AB$ и $BC$ равностороннего треугольника $ABC$ взяты точки $D$ и $K$ соответственно, а на стороне $AC$ — точки $E$ и $M$ так, что суммы $DA + AE$ и $KC + CM$ равны стороне треугольника. Докажите, что угол между прямыми $DM$ и $KE$ равен $∘ 60 .$

Показать доказательство

Пусть сторона треугольника равна $a$ . Тогда $KC = a− CM = AM$ и $AD =a − AE = CE$ .

$PIC$

Значит, треугольники $CKE$ и $AMD$ равны. Пусть $F$ — точка пересения $DM$ и $EK,$ тогда $∠MEF = ∠ADM = 120∘− ∠EMF,$ и значит, $∠MF E = 60∘$ .

Ошибка.
Попробуйте повторить позже

Задача 10#91923

Треугольник $ABC$ — равносторонний. Докажите, что для любой точки $M$ плоскости выполнено неравенство $MA +MB ≥MC.$

Показать доказательство

Напишем неравенство Птолемея.

AB ⋅CM ≤AC ⋅BM + BC ⋅AM

Сократим на $AB =BC = AC$ .

CM ≤ MB + MA

Ошибка.
Попробуйте повторить позже

Задача 11#78104

Дан правильный треугольник $ABC.$ На стороне $AB$ отмечена точка $K,$ на стороне $BC$ — точки $L$ и $M$ ( $L$ лежит на отрезке $BM$ ) так, что $KL = KM,BL = 2,AK =3.$ Найдите $CM.$

Источники: ММО-2021, 7.5(см. mmo.mccme.ru)

Показать ответ и решение

Решение 1.

$PIC$

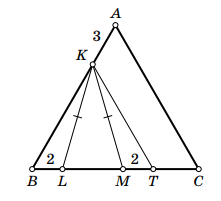
Отметим на продолжении отрезка $LM$ за точку $M$ такую точку $T,$ что $MT = 2.$ Углы $BLK$ и $T MK$ равны, так как они смежные с равными углами равнобедренного треугольника $KLM.$ Значит, треугольники $BLK$ и $TMK$ равны по двум сторонам и углу между ними. Тогда равны их соответствующие углы: $∠KT M = ∠KBL = 60∘.$

В треугольнике $KBT$ два угла по $60∘,$ поэтому он равносторонний, и $BK = BT.$ Так как треугольник $ABC$ тоже равносторонний и $BA = BC,$ то

CT = BC − BT = BA − BK =AK = 3

(и точка $T$ лежит именно на стороне $BC,$ а не на ее продолжении). Тогда

CM = CT +MT =3 +2 =5

Решение 2.

$PIC$

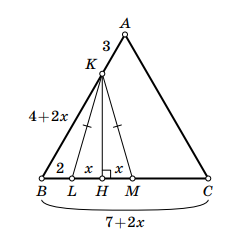
Проведем высоту $KH$ равнобедренного треугольника $KLM.$ Она также является его медианой, поэтому $LH = HM.$ Обозначим $LH = HM =x.$ Треугольник $KBH$ — прямоугольный с углом $B,$ равным $∘ 60,$ а значит, его гипотенуза $KB$ в $2$ раза больше его катета $BH.$ Так как $BH = 2+ x,$ то $KB = 2BH =4 +2x,$ а тогда

BA = BK + KA = 4+2x+ 3= 7+ 2x

Треугольник $ABC$ равносторонний, поэтому $BC = BA = 7+ 2x.$ А значит,

MC = BC − BM = (7+ 2x)− (2+ 2x)=5

Ответ:

$5$

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#78105

Точка $M$ — середина стороны $AC$ равностороннего треугольника $ABC.$ Точки $P$ и $R$ на отрезках $AM$ и $BC$ соответственно выбраны так, что $AP$ = $BR.$ Найдите сумму углов $ARM, PBM$ и $BMR.$

Источники: Олимпиада Эйлера, 2021, РЭ, 7 задача(см. old.mccme.ru)

Показать ответ и решение

$PIC$

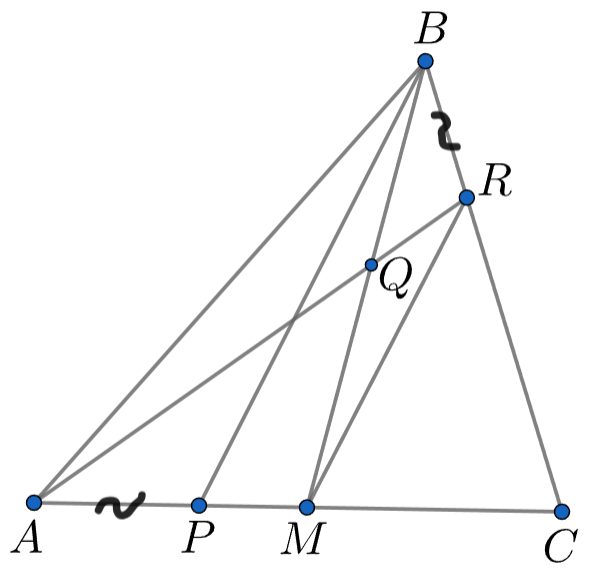
Пусть отрезки $AR$ и $BM$ пересекаются в точке $Q.$ . Так как треугольники $ABP$ и $BAR$ равны по первому признаку, $∠BAR =∠ABP =α.$ Тогда

∠ARM + ∠BMR = 180∘− ∠AQB =2α +∠P BM

(здесь первое равенство — теорема о внешнем угле для треугольника $MQR,$ а второе — теорема о сумме углов для треугольника $AQB$ ), откуда

∠ARM + ∠BMR +∠P BM = 2(α +∠P BM )=2∠ABM = 60∘

Ответ:

$60∘$

Ошибка.
Попробуйте повторить позже

Задача 13#38694

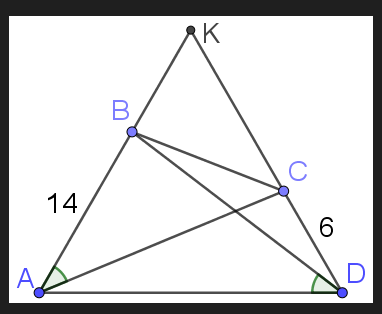
Выпуклый четырёхугольник $ABCD$ таков, что $∠BAC = ∠BDA$ и $∠BAD = ∠ADC =60∘$ . Найдите длину $AD$ , если известно, что $AB = 14,CD = 6.$

Источники: Школьный этап - 2019, Москва, 8.6

Подсказки к задаче

Подсказка 1

Два прилежащих угла четырёхугольника равны по 60 градусов. Какое удобное дополнительное построение можно сделать, чтобы получить эти углы уже в треугольнике?

Подсказка 2

Конечно, продлить AB и CD до пересечения в точке K и получить равносторонний треугольник. Поэтому можно искать не AD, а, например, KA или KD, так как они равны. Как теперь воспользоваться равенством углов ∠ BAC и ∠ BDA?

Подсказка 3

Докажите равенство треугольников △KCA и △BAD

Показать ответ и решение

Продлим стороны $AB$ и $CD$ до пересечения в точке $K$ . Заметим, что $∠KAD = ∠KDA = 60∘$ , а значит, треугольник — равносторонний. Тогда треугольники $KCA$ и $BAD$ равны по двум углам: $∘ ∠AKC =∠BAD = 60$ , $∠KAC =∠BDA$ по условию; и прилежащей стороне: $AK = AD$ . Тогда $KC =AB = 14$ и сторона равностороннего треугольника равна $KC + CD = 20$ , а значит, и $AD = 20.$

$PIC$

Ответ: 20

Ошибка.
Попробуйте повторить позже

Задача 14#89601

Дан равносторонний треугольник $ABC.$ Точка $D$ выбрана на продолжении стороны $AB$ за точку $A,$ точка $E$ — на продолжении $BC$ за точку $C,$ а точка $F$ — на продолжении $AC$ за точку $C$ так, что $CF = AD$ и $AC + EF = DE.$ Найдите угол $BDE.$

Источники: Олимпиада Эйлера, 2016, ЗЭ, 3 задача(см. old.mccme.ru)

Подсказки к задаче

Подсказка 1

Один отрезок равен сумме двух других, очень уж хочется воспользоваться этим условием. Но и углы по 60 градусов хотелось бы использовать. Нужно грамотное дополнительное построение.

Подсказка 2

Предлагается достроить ACE до параллелограмма ACEG, у него известные углы, да и появляется новый отрезок длины AC. Но нам то было бы хорошо, если G лежала бы на ED (Чтобы ED выложить из двух в сумме его дающих). А может быть так и оказалось?

Подсказка 3

Действительно, рассмотрим треугольники CFE и ADG, они равны по двум сторонам и углу между ними, а, значит, G обладает свойством GD+GH=AC+EF=DE. Осталось сделать верный вывод об искомом угле.

Показать ответ и решение

Достроим треугольник $ACE$ до параллелограмма $ACEG.$ Тогда $AG = CE,CF = AD,$ угол

∘ ∘ ∘ ∘ ∘ GAD = 180 − ∠BAC − CAG = 180 − 60 − (180 − ∠ACE )= 60 =∠BCA =∠ECF

Значит, треугольники $CF E$ и $ADG$ равны по трём сторонам. То есть

GD = EF ⇒ ED = AC +EF = EG +GD ⇒ G

лежит на отрезке $ED.$ Значит $DE∥AC ⇒ ∠BDE =∠BAC =60∘$

$PIC$

Ответ:

$60∘$

Ошибка.
Попробуйте повторить позже

Задача 15#39611

На плоскости задана точка $P$ . Рассматриваются различные равносторонние треугольники $ABC$ , такие что $PA =2,PB = 3.$ Какое максимальное значение может принимать длина отрезка $P C?$

Источники: ОММО-2013, номер 7, (см. olympiads.mccme.ru)

Подсказки к задаче

Счётный способ, подсказка 1

Заметим, что если зафиксировать треугольник PAB, то картинка определяется единственным образом. Как его зафиксировать?

Счётный способ, подсказка 2

Конечно, можно ввести лишь три его стороны, но лучше ввести еще и два угла, чтобы счет проходил легче(а с помощью теорем синусов или косинусов, мы всегда сможем связать углы со сторонами при желании).

Счётный способ, подсказка 3

Выразите сторону AB по теореме косинусов и угол PBA через стороны треугольника PAB и угол APB. Выразили? Кажется, все готово, чтобы считать PC.

Счётный способ, подсказка 4

Попробуйте привести выражение PC к такому виду, чтобы только одно слагаемое было переменным, а все остальное являлось константой.

Геометрический способ, подсказка 1

На картинке есть угол 60 градусов и два равных отрезка исходящих из него(AB и AC). Это очень сильно намекает на поворот в этой точке.

Геометрический способ, подсказка 2

Да, нужно сделать поворот на 60 градусов, переводящий точку B в точку C. Это удобно, так как точка P переедет в точку P’,при этом APP’-равносторонний и треугольники AP’C и APB равны. Какой вывод о длине PC можно сделать?

Геометрический способ, подсказка 3

Да, по неравенству треугольника PC<=5. Осталось лишь привести пример, но как? Попробуйте делать те же действия, как вы получили оценку, но в обратном порядке, не забывая о том, когда эта оценка достигается(расположение точек P,P’,C)

Показать ответ и решение

$PIC$

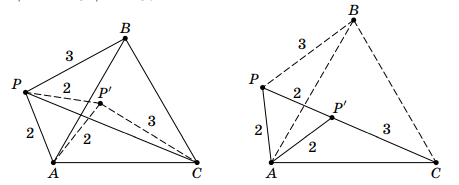
Первое решение.

Докажем, что длина не больше $5$ . Для этого рассмотрим поворот с центром в точке $A$ на $60∘$ таким образом, что $B$ переходит в $C$ . Точка $P$ переходит в $P′$ , а поскольку $AP = AP′ = 2$ и $∠P AP′ = 60∘$ , то $PP′ = 2$ , откуда $P C ≤ P′C+ P′P = PB + P′P = 5$ по неравенству треугольника.

Для построения примера сначала построим правильный $△AP P′$ , затем на продолжении $PP′$ отметим $C :CP′ = 3$ . Наконец, построим правильный треугольник $ABC$ на отрезке $AC$ . Остаётся показать, что выполнено $PB = 3$ , но для этого достаточно рассмотреть поворот на $60∘$ в обратную сторону $C → B$ , тогда отрезок $P′C = 3$ перейдёт в $PB$ .