Проведение параллельных прямых
Ошибка.
Попробуйте повторить позже
В параллелограмме выбрана точка
такая, что угол
вдвое больше угла
а угол
вдвое больше угла
Доказать, что длины отрезков
и
равны.
Источники:
Подсказка 1
Нам известно, что некоторые углы на чертеже в два раза больше других. Но как это может нам помочь? Для чего это вообще дано? Вспомните, какие есть геометрические конструкции, в которых одни углы в два раза больше других.
Подсказка 2
Посмотрим на окружность: в ней центральные углы в два раза больше вписанных. Давайте и в нашей задаче построим какую-нибудь окружность так, чтобы "маленькие" углы были для неё вписанными.
Подсказка 3
Рассмотрим окружность, описанную около треугольника ADP, а также её центр. Поотмечайте уголочки и найдите равные.
Подсказка 4
Так, есть равнобедренные треугольники и равные углы, но что с этим делать? Вот было бы удобно, если бы ABPM был параллелограммом... Постойте, а если это действительно так?
Подсказка 5
Постройте параллелограмм ABPO и докажите, что точки O и M совпадают. Тогда останется только отметить равные стороны и радоваться решённой задаче!
Пусть
Проведем из точки
отрезок
параллельный и равный стороне
так, чтобы образовались два
параллелограмма
и
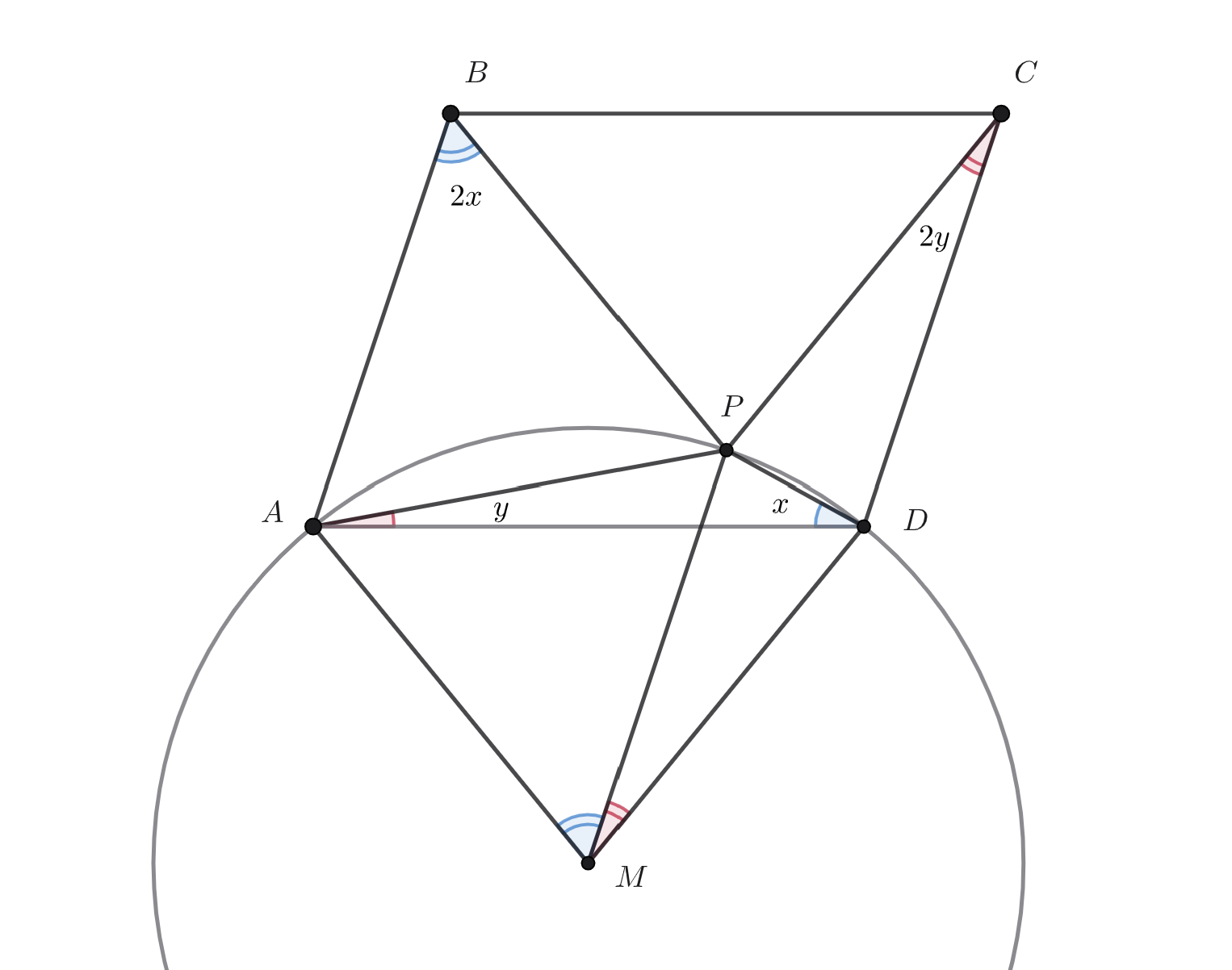
Рассмотрим описанную окружность треугольника с центром
Угол
равен
и является вписанным, тогда
Следовательно, точка
принадлежит описанной окружности треугольника
Аналогично, точка
принадлежит
описанной окружности треугольника
следовательно,
является пересечением этих окружностей и совпадает с
Тогда длины
отрезков
и
совпадают с длиной радиусов
и
описанной окружности треугольника
и равны между
собой.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




