Проведение параллельных прямых
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
Углы при большем основании трапеции равны и
а меньшая боковая сторона равна
Найдите разность оснований.
Подсказка 1:
Попробуйте найти на рисунке отрезок, равный разности оснований.
Подсказка 2:
Чтобы это сделать, нужно на большем основании с одного из концов отметить отрезок, равный меньшему основанию. Тогда оставшаяся часть будет разностью. Как это сделать?
Подсказка 3:
Можно сделать параллельный перенос отрезка BC на прямую AD так, чтобы точка B перешла в точку A. На какой вектор надо перенести, чтобы так получилось?
Пусть и
— основания трапеции
причем
Через вершину проведем прямую, параллельную боковой стороне
Пусть эта прямая пересекает основание
в точке
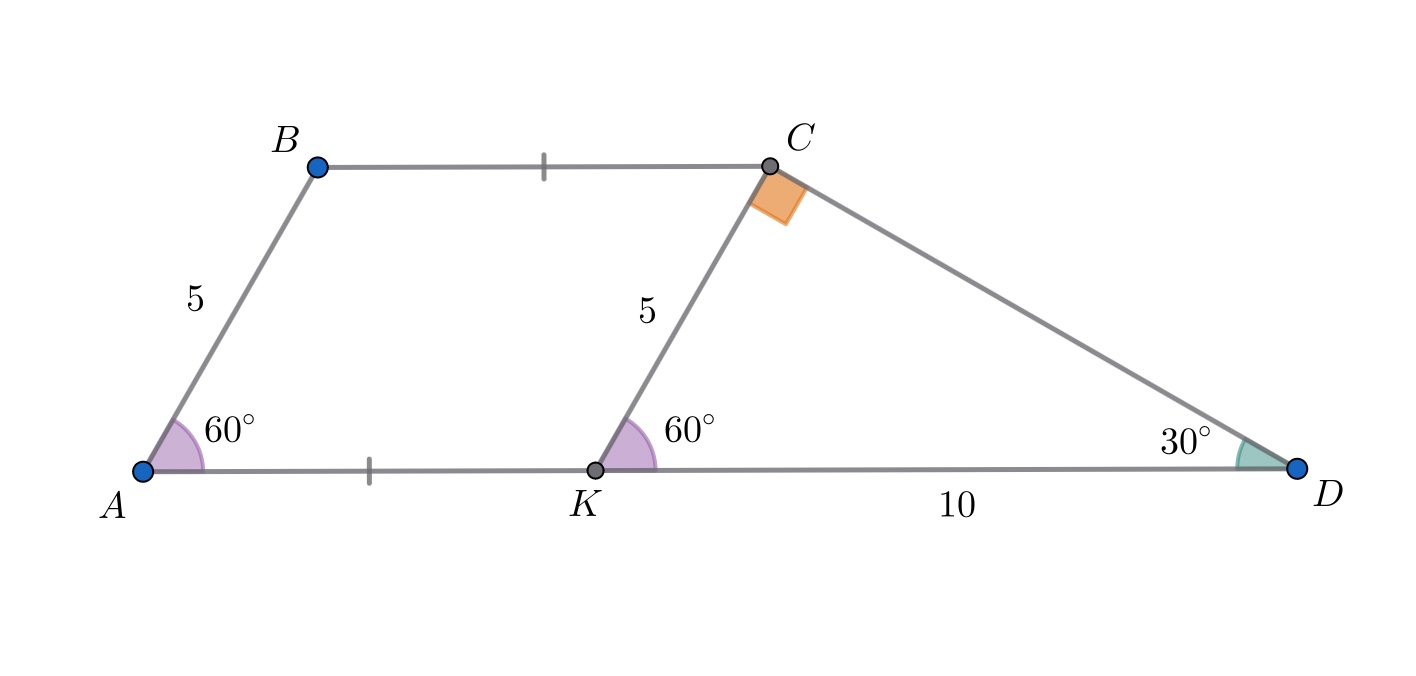
Тогда — параллелограмм. Поэтому получаем следующие равенства отрезков:
Из равенства соответственных углов получаем:
В прямоугольном треугольнике катет
лежит против угла в
следовательно,
Ошибка.
Попробуйте повторить позже
В равнобедренном треугольнике (
) проведена биссектриса
На основании
отмечена точка
так,
что
Точка
выбрана таким образом, что четырёхугольник
—– параллелограмм. Докажите, что
Источники:
Подсказка 1:
У вас должно возникнуть желание продлить ED до пересечения с AC в точке X. Почему? Во-первых, эта прямая будет отсекать равнобдренный треугольник от ABC. Во-вторых, имеется биссектриса DC и можно будет удачно перекинуть углы. Поработайте с этой картинкой.
Подсказка 2:
Скорее всего, у вас возникает желание доказать через счёт углов, что треугольник EBF равнобедренный. Попробуйте пойти другим путём. Найдите какую-нибудь пару равных треугольников, в которых отрезки BE и BF являются соответствующими сторонами.
Подсказка 3:
Обратите внимание на треугольники BXE и FCB.
Первое решение. Продолжим отрезок до пересечения со стороной
в точке
Поскольку
треугольник
равнобедренный. Кроме того,
поэтому треугольник также равнобедренный, и
Из параллелограмма
получаем
Тогда
Поскольку получаем, что треугольники
и
равны по двум сторонам и углу между ними, откуда и
следует, что
![]()
_________________________________________________________________________________________________________________________________________________________________________________
Второе решение. Пусть описанная окружность треугольника пересекает вторично прямую
в точке
Тогда
также, поскольку —– (внутренняя или внешняя) биссектриса угла
имеем
Поэтому треугольники и
равны. Отсюда следует, что
а тогда и треугольники и
также равны. Значит,
Кроме того, из полученного равенства углов
и
следует, что
Тогда треугольники и
также равны, и
что и требовалось.
![]()
Ошибка.
Попробуйте повторить позже
Диагонали выпуклого четырёхугольника пересекаются в точке
Точки касания описанных окружностей треугольников
и
с их общими внешними касательными лежат на окружности
Точки касания описанных окружностей треугольников
и
с их общими внешними касательными лежат на окружности
Докажите, что центры окружностей
и
совпадают.
Источники:
Подсказка 1:
Давайте введём следующие обозначения: O_{AB}, O_{BC}, O_{CD}, O_{AD} — центры окружностей (ABE), (BCE), (CDE), (ADE), a T₁, T₂ — точки касания одной из внешних касательных к окружностям, описанным около ABE и CDE. Обратите внимание на прямоугольную трапецию O_{AB}T₁T₂O_{CD}. В частности, на середину O_{AB}O_{CD}. Что можно про неё сказать?
Подсказка 2:
Если сделать симметрию относительно точки O, во что перейдет окружность ω? Какие выводы можно сделать?
Подсказка 3:
Точка O — центр ω. Аналогичные рассуждения можно проделать с серединой O_{AD}O_{BC}. Значит, мы хотим показать, что середины отрезков O_{AD}O_{BC} и O_{AB}O_{CD} совпадают. А что для этого достаточно доказать?
Подсказка 4:
Достаточно доказать, что четырехугольник O_{AB}O_{BC}O_{CD}O_{AD} — параллелограмм. Попробуйте для этого показать, что его противолежащие стороны параллельны.
Обозначим центры описанных окружностей треугольников
через
соответственно. Пусть
— точки касания одной из общих касательных с описанными окружностями треугольников
и
соответственно; обозначим через
и
середины отрезков
и
соответственно. Тогда в прямоугольной
трапеции
прямая
— средняя линия, поэтому она является серединным перпендикуляром к отрезку
Заметим,
что окружность
симметрична относительно прямой
на которой также лежит точка
значит,
— центр
![]()
Аналогично получаем, что середина отрезка является центром
Поэтому утверждение задачи равносильно тому, что
— параллелограмм. Для доказательства этого достаточно заметить, что
и
— серединные
перпендикуляры к отрезкам
и
поэтому
аналогично,
откуда и следует
требуемое.
![]()
Ошибка.
Попробуйте повторить позже
В прямоугольном треугольнике угол
прямой. На катете
выбрана точка
так, что
а на катете
выбрана
точка
так, что
Найдите острый угол между прямыми
и
.png)
Достроим треугольник до прямоугольника
и выберем на его стороне
точку
так, что
параллельно
Тогда
и прямоугольные треугольники
и
равны, причём
Поэтому
и
то есть
— равнобедренный прямоугольный треугольник. Значит,
и, в силу параллельности прямых
и
острый угол между прямыми
и
тоже составляет
градусов.
Ошибка.
Попробуйте повторить позже
На медиане треугольника
нашлась такая точка
что
Кроме того,
Докажите, что
Проведём через точку прямую, параллельную
Отметим на ней точку
так, что
Заметим, что
—
параллелограмм. Значит, достаточно доказать, что
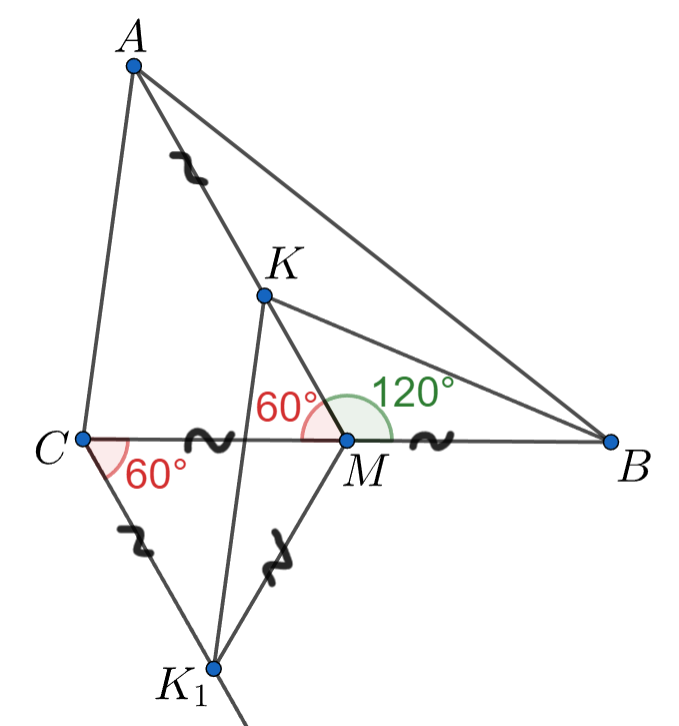
Углы и
равны (по
) как противолежащие. Значит, треугольник
равносторонний. Таким образом,
Также нетрудно видеть, что
Значит, треугольники
и
равны по первому
признаку (
— общая сторона). Отсюда вытекает равенство
и
Ошибка.
Попробуйте повторить позже
В трапеции , где
угол
равен сумме углов
и
На продолжении отрезка
за вершину
отложен отрезок
Докажите, что
![]()
Отложим на луче отрезок
Тогда четырёхугольник
— параллелограмм, поэтому
. Используя
условие, получаем
значит, треугольник — равнобедренный,
Далее, поскольку
получаем
Так как прямая
является биссектрисой угла
и, тем самым, серединным перпендикуляром к основанию
равнобедренного треугольника
Поэтому точка K равноудалена от концов отрезка
что и требовалось
доказать
Ошибка.
Попробуйте повторить позже
Точка, расположенная на основании трапеции, соединена с вершинами другого основания. Построенные отрезки делят трапецию на три треугольника равного периметра. Докажите, что данная точка — середина основания.
Подсказка 1
Периметры всех трёх треугольников равны, а ещё есть параллельность оснований трапедции. Вместо того, чтобы при решении пользоваться лишь равенством периметров, попробуем доказать более сильное условие на эти три треугольника. Какой есть простой случай, когда периметры трёх треугольников точно будут равными?
Подсказка 2
Докажем, что из условия следует, что все три треугольника равны и две пары “соседних” образуют параллелограммы. Можно попробовать доказать это методом от противного!
Подсказка 3
Возьмём два соседних треугольника и предположим, что они не образуют параллелограмм. Тогда отметим на одном из оснований трапедции точку так, чтобы треугольник достроился до параллелограмма. Теперь вспомним неравенство треугольника, равенство периметров и найдём здесь противоречие!
Пусть — трапеция с основанием
на котором выбрали точку
Тогда достаточно доказать, что
и
—
параллелограммы. Достроим треугольник
до параллелограмма
![]()
Тогда периметры треугольников и
равны, поэтому равны периметры треугольников
и
Следовательно,
так как иначе один из треугольников
и
лежит внутри другого и их периметры не могут быть равны. Поэтому
— параллелограмм. Аналогично доказывается, что
— параллелограмм. Тогда
и будет серединой основания и к тому же
Ошибка.
Попробуйте повторить позже
Дан равносторонний треугольник На сторонах
и
выбраны точки
и
соответственно так, что
и
Докажите, что
Подсказка 1
Отметим на AC точку P такую, что ZP || AB. Попробуйте найти теперь отрезок, с отмеченной серединой.
Подсказка 2
После того, как вы нашли, что Y - середина отрезка AP, надо медиану продлить! Продлим ZY до пересечения с AB. Обозначим точку пересечения за K. Попробуйте найти треугольник, в котором медиана совпадает с высотой.
Подсказка 3
Теперь осталось только по перекладывать отрезки и воспользоваться тем, что треугольник PZC правильный.
Через точку параллельно стороне
проведём прямую до пересечения со стороной
в точке
Тогда треугольник
—
также равносторонний, поэтому
и
то есть
— середина отрезка
Продолжим катет
до
пересечения с прямой
в точке
Тогда треугольники
и
равны по стороне и двум углам
поэтому
а
середина отрезка
Треугольник
— равнобедренный, так как его высота
является
медианой. Следовательно,
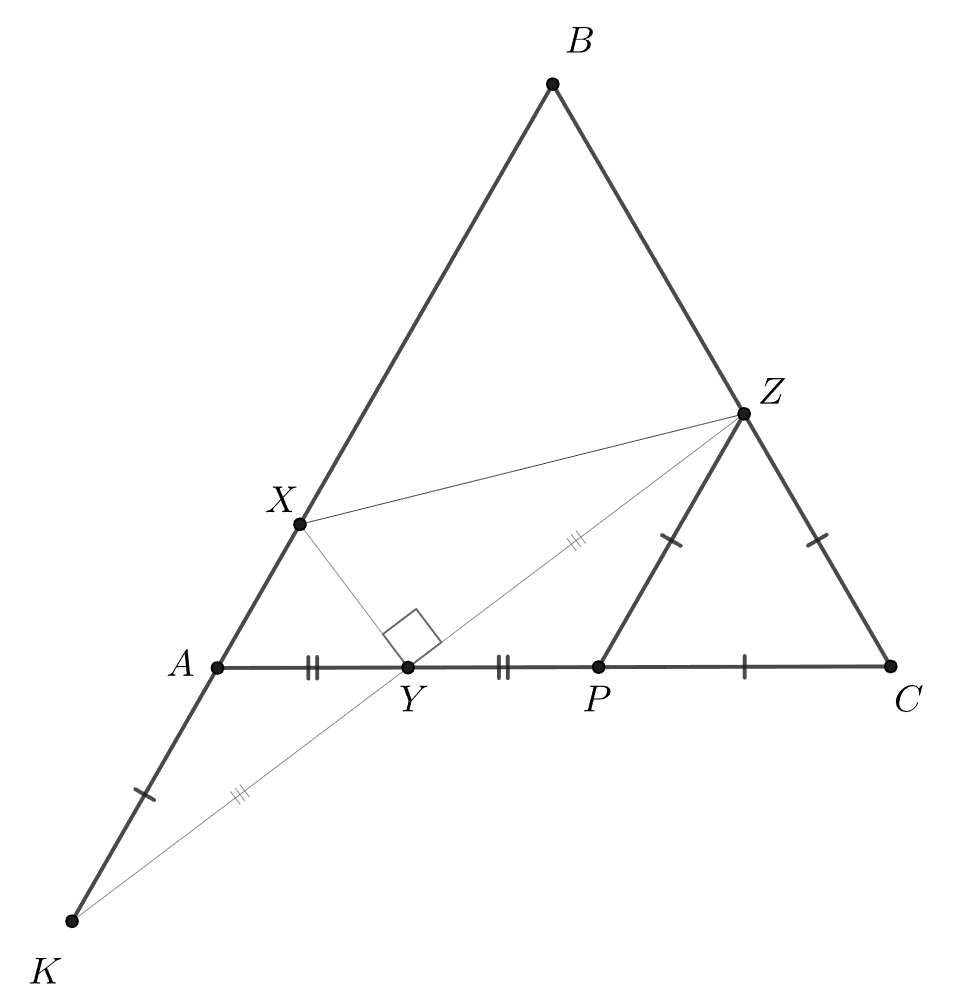
Ошибка.
Попробуйте повторить позже
На плоскости дан четырёхугольник строго внутри него выбрана точка
Известно, что
является параллелограммом, а
также
Докажите равенство
Давайте достроим треугольник до параллелограмма
.
Тогда , поэтому четырёхугольник
вписанный, следовательно,
![]()
Теперь давайте посмотрим на треугольники и
. Ясно, что второй является образом первого при параллельном переносе на
вектор
. Значит,
. А из этого равенства следует требуемое в условии добавлением
к обеим частям
равенства.
Ошибка.
Попробуйте повторить позже
В параллелограмме выбрана точка
такая, что угол
вдвое больше угла
а угол
вдвое больше угла
Доказать, что длины отрезков
и
равны.
Источники:
Подсказка 1
Нам известно, что некоторые углы на чертеже в два раза больше других. Но как это может нам помочь? Для чего это вообще дано? Вспомните, какие есть геометрические конструкции, в которых одни углы в два раза больше других.
Подсказка 2
Посмотрим на окружность: в ней центральные углы в два раза больше вписанных. Давайте и в нашей задаче построим какую-нибудь окружность так, чтобы "маленькие" углы были для неё вписанными.
Подсказка 3
Рассмотрим окружность, описанную около треугольника ADP, а также её центр. Поотмечайте уголочки и найдите равные.
Подсказка 4
Так, есть равнобедренные треугольники и равные углы, но что с этим делать? Вот было бы удобно, если бы ABPM был параллелограммом... Постойте, а если это действительно так?
Подсказка 5
Постройте параллелограмм ABPO и докажите, что точки O и M совпадают. Тогда останется только отметить равные стороны и радоваться решённой задаче!
Пусть
Проведем из точки
отрезок
параллельный и равный стороне
так, чтобы образовались два
параллелограмма
и
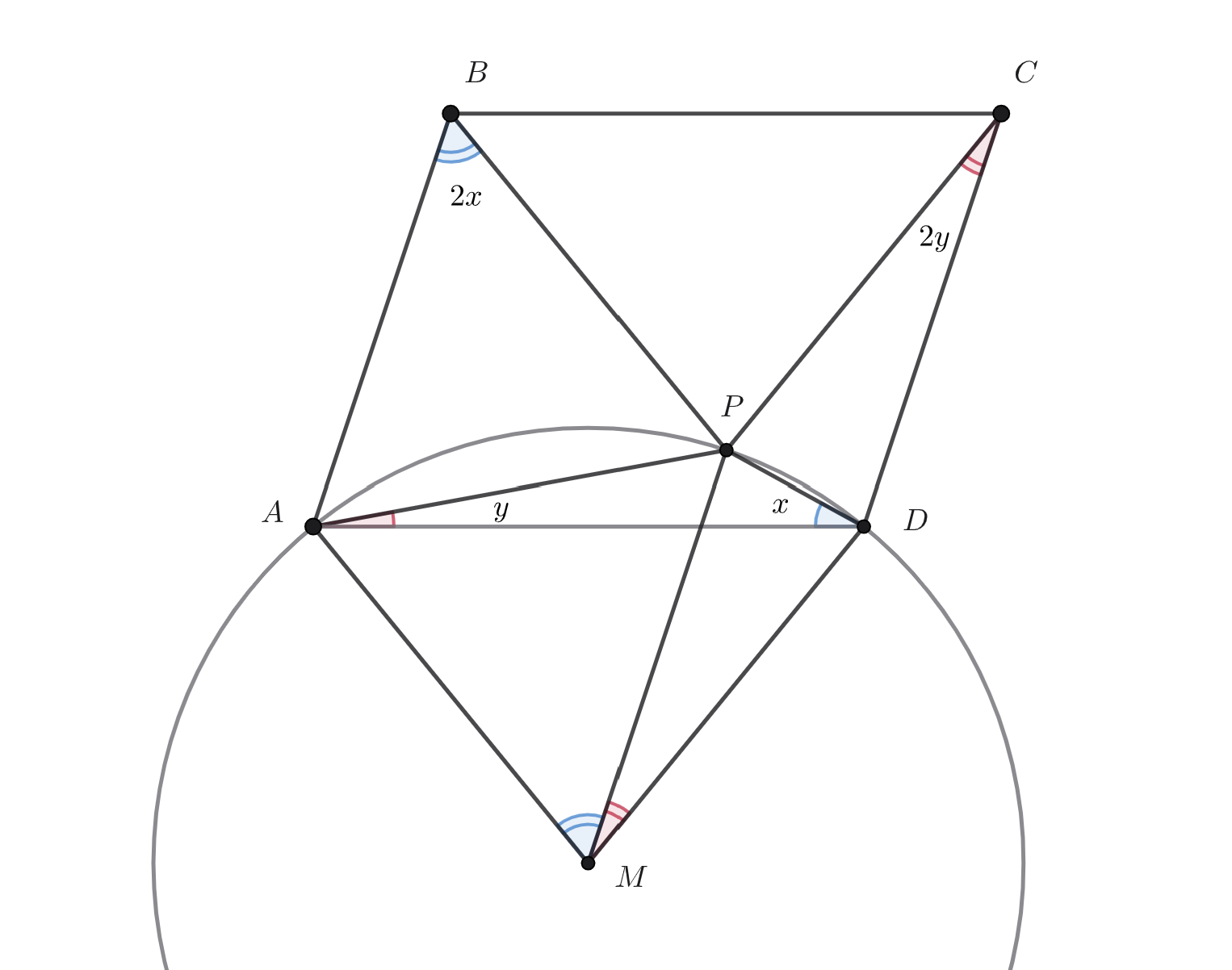
Рассмотрим описанную окружность треугольника с центром
Угол
равен
и является вписанным, тогда
Следовательно, точка
принадлежит описанной окружности треугольника
Аналогично, точка
принадлежит
описанной окружности треугольника
следовательно,
является пересечением этих окружностей и совпадает с
Тогда длины
отрезков
и
совпадают с длиной радиусов
и
описанной окружности треугольника
и равны между
собой.
Ошибка.
Попробуйте повторить позже
Точка — середина стороны
треугольника
, а точка
— середина медианы
. Прямая, проходящая через точку
параллельно
пересекает сторону
в точке
. Найдите отношение
Подсказка 1
Пусть AQ пересекает BC в точке R. Так сразу найти какое-то отношение AQ к MP не выглядит простой задачей. Давайте сначала попробуем выразить AR и QR через MP.
Подсказка 2
В условии даны сразу несколько середин сторон, так еще и про параллельность что-то сказали. Возможно, стоит задуматься о каких-то средних линиях.
Подсказка 3
MP проходит через середину AC параллельно AQ, значит, MP – средняя линия треугольника ARC. QR проходит через середину BM параллельно MP, значит, QR – средняя линия треугольника MBP.
Пусть пересекается с
в точке
.
Первое решение.
.jpg)
Прямая, проходящая через середину отрезка
параллельно
, это средняя линия треугольника
, она равна половине
. То есть
Прямая, проходящая через точку отрезка
параллельно
, это средняя линия треугольника
, она равна половине
. То есть
В итоге
__________________________________________________________________________________________________
Второе решение.
Мы видим медиану и хочется немедленно её удвоить.
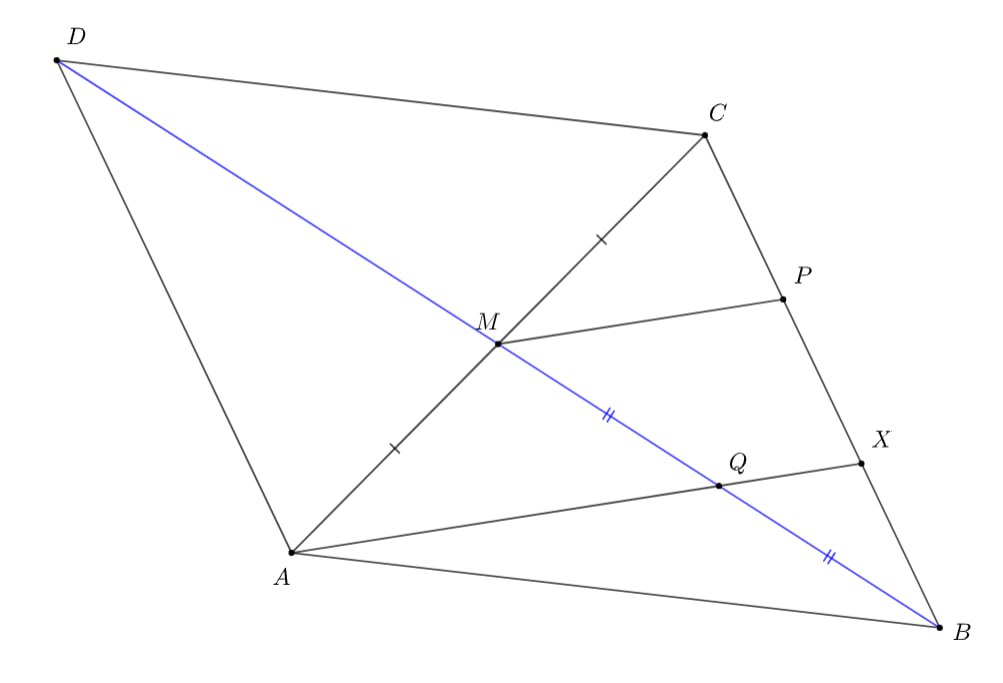
Тогда мы получаем параллелограмм и за счёт равенства накрест лежащих углов при параллельных прямых
с
коэффициентом подобия
Из подобия мы выяснили, что
Прямая, проходящая через точку параллельно
, это средняя линия треугольника
, она равна половине
. В
итоге
__________________________________________________________________________________________________
Третье решение.
.jpg)
По теореме Менелая для треугольника и прямой
По теореме Менелая для треугольника и прямой
Прямая, проходящая через точку параллельно
, это средняя линия треугольника
, она равна половине
. В
итоге
Ошибка.
Попробуйте повторить позже
На сторонах треугольника внешним образом построили параллелограммы
,
и
. Докажите, что из отрезков
,
и
можно составить треугольник.
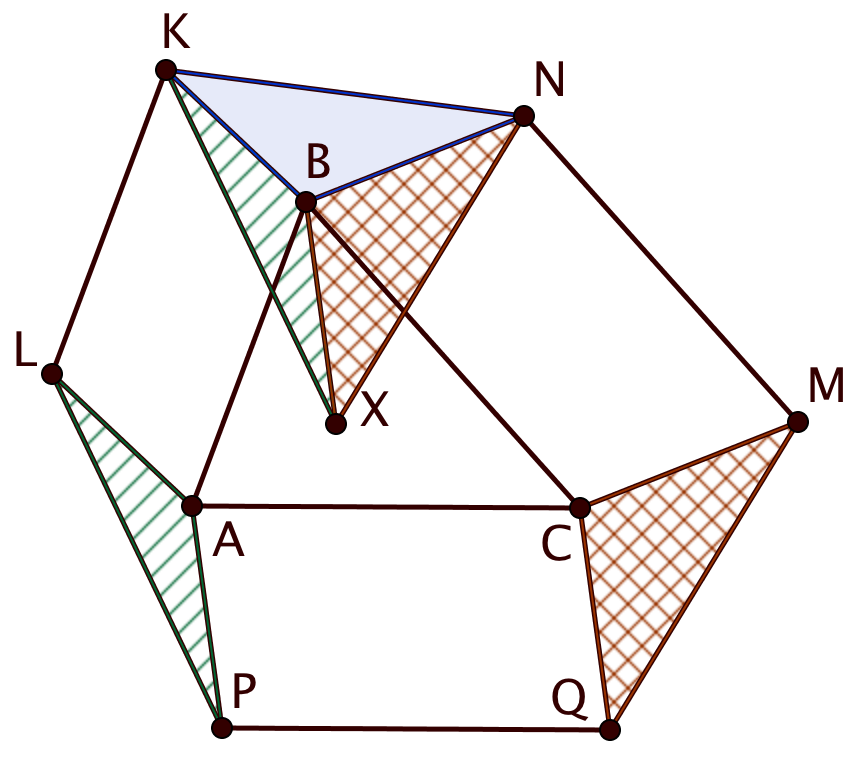
Отложим от точки отрезок
, равный и параллельный
. Рассмотрим треугольники
и
. В них
и
как противоположные стороны параллелограмма, и
,
по построению. Поэтому
, и
по двум сторонам и углу между ними.
Аналогично . Теперь в треугольнике
стороны
,
и
равны соответственно отрезкам
,
и
, значит, из последних можно составить треугольник.
Ошибка.
Попробуйте повторить позже
Биссектриса угла при основании равнобедренного треугольника делит противолежащую сторону так, что отрезок, прилежащий к вершине треугольника, равен его основанию. Докажите, что эта биссектриса также равна основанию треугольника.
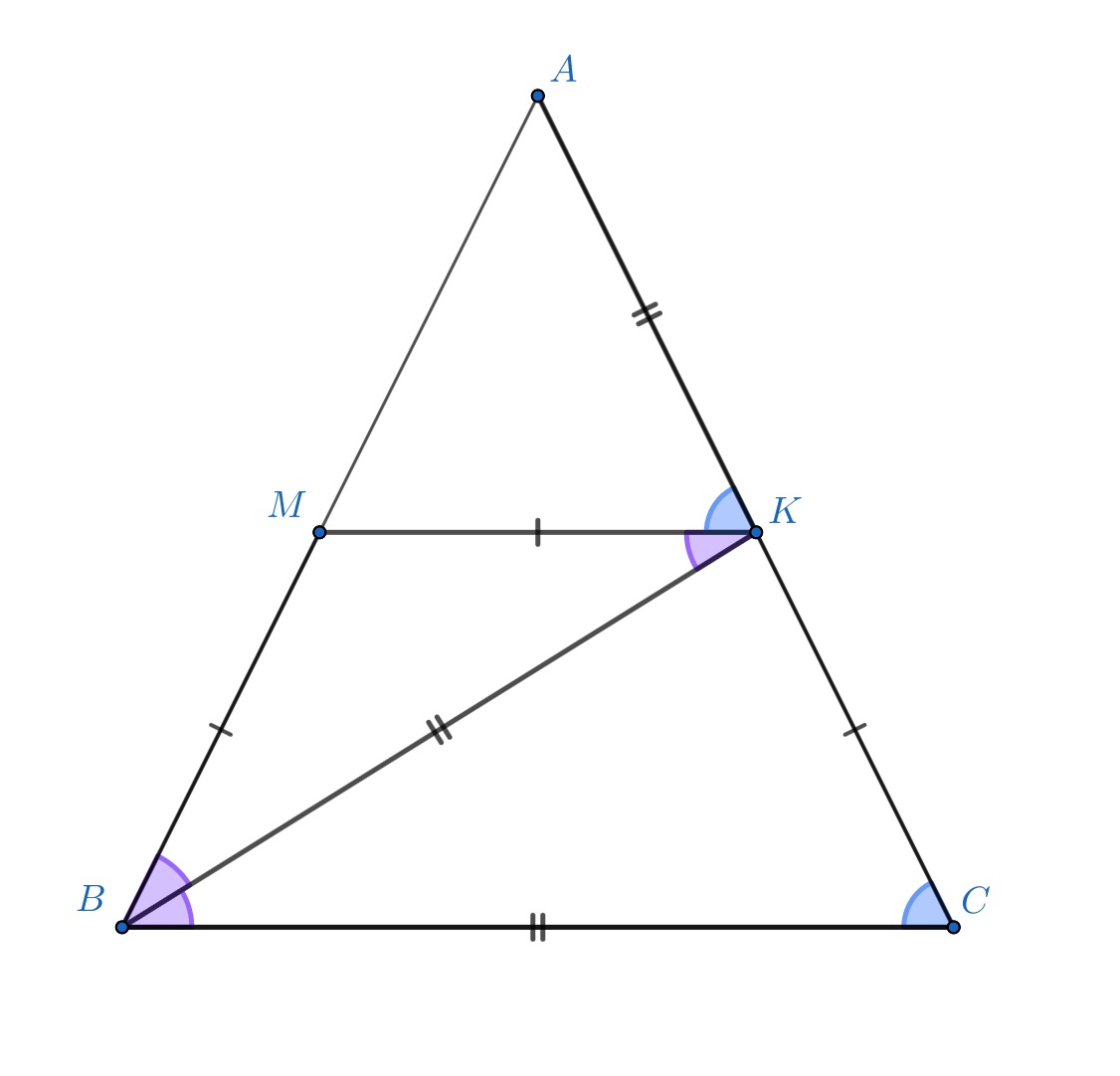
Пусть — биссектриса угла
при основании
равнобедренного треугольника
Через точку проведём прямую, параллельную основанию
Пусть
— точка пересечения этой прямой с боковой стороной
Тогда
Поэтому треугольник
— равнобедренный. Следовательно,
а так как
и
то треугольники
и
равны по двум сторонам и углу между ними. Значит, треугольник
также равнобедренный, то есть
Ошибка.
Попробуйте повторить позже
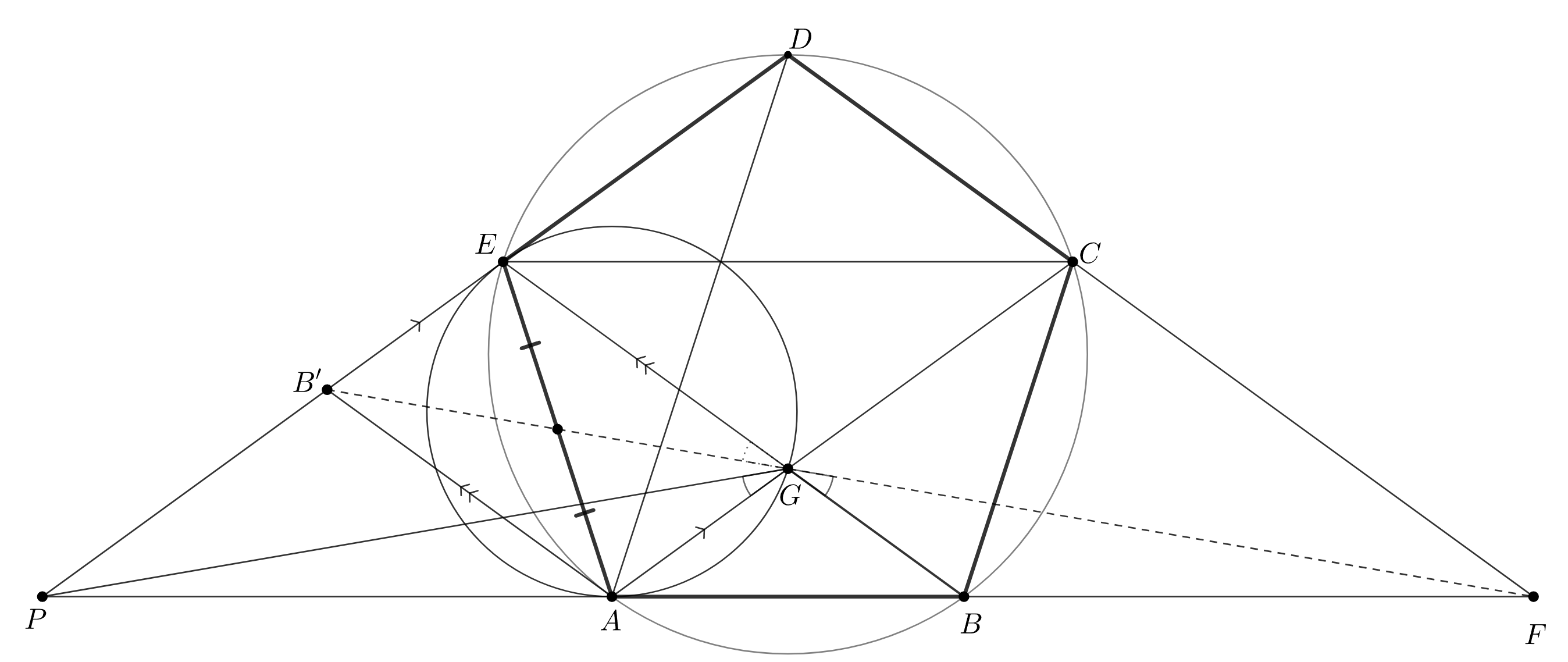
Дан правильный пятиугольник Точки
и
являются точками пересечения прямых
и
и
и
соответственно. Докажите, что
Подсказка 1
Удвоенный угол напоминаем нам о биссектрисе угла BHF - попробуем доказать, что ею является прямая, проходящая через H и параллельная EF. Понятно, что EF перпендикулярна AD - тогда какой факт, связанный с точкой B, мы можем доказывать?
Проведем через точку прямую
параллельную
Достаточно показать, что
является биссектрисой угла
Поскольку
верно, что
Таким образом, достаточно показать, что
является биссектрисой внешнего угла
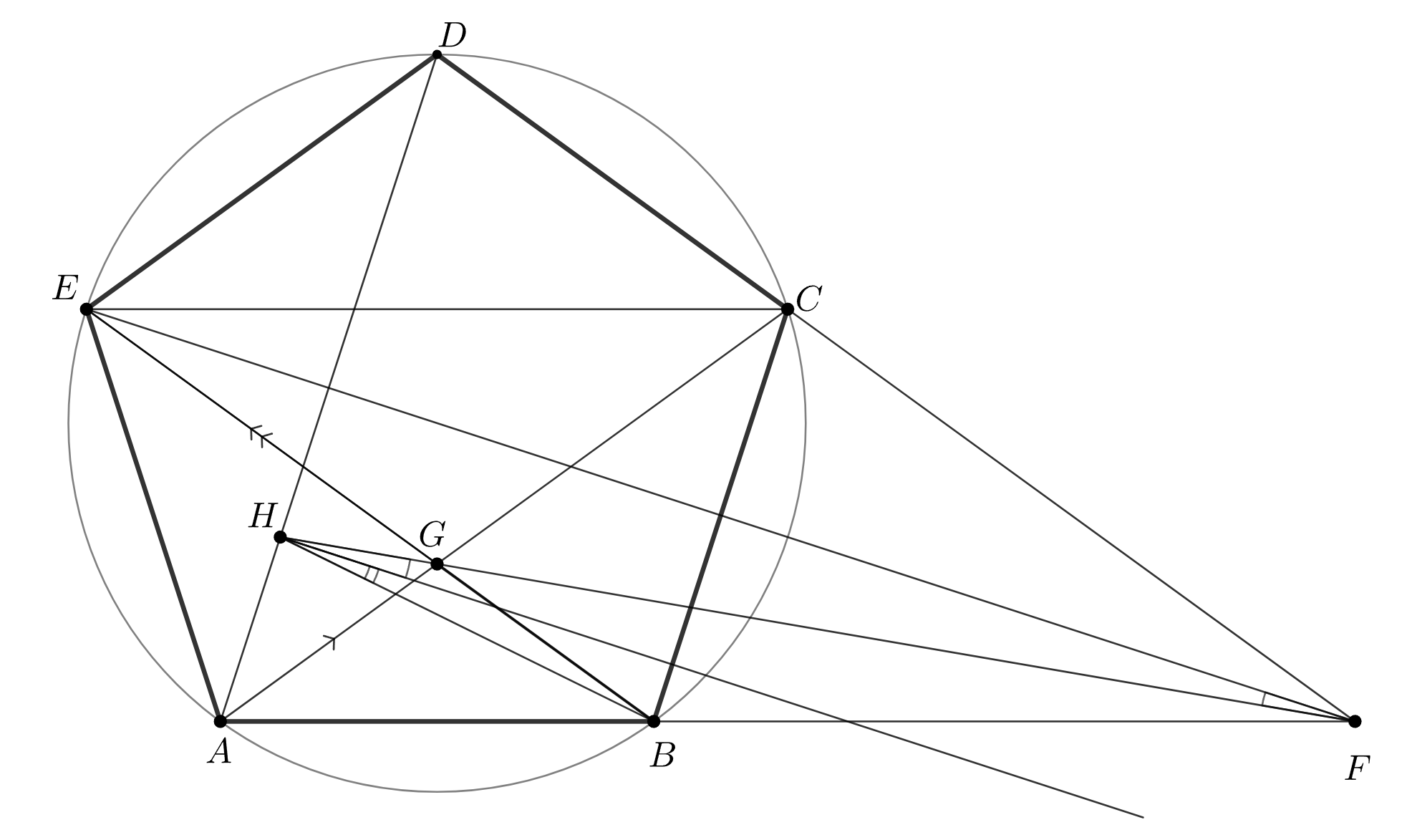
Последнее эквивалентно условию принадлежности точки симметричной
относительно
прямой
Пусть — окружность описанная около пятиугольника
Заметим, что прямые
и
симметричны относительно
прямой
поскольку
т.к. данные углы опираются на равные дуги в окружности
Таким образом,
лежит на
прямой
то есть
Кроме этого в силу симметрии и равенства дуг в окружности
следовательно
Заключаем, что точка — параллелограмм, откуда
— медиана в треугольнике.
Пусть — точка, симметричная
относительно
Осталось показать, что
Докажем. что
является
точкой пересечения касательных в точках
и
к окружности
как следствие является симедианой треугольника
Действительно ведь каждый из углов равен сумме двух половин дуг, равных дуге
в
окружности
Ошибка.
Попробуйте повторить позже
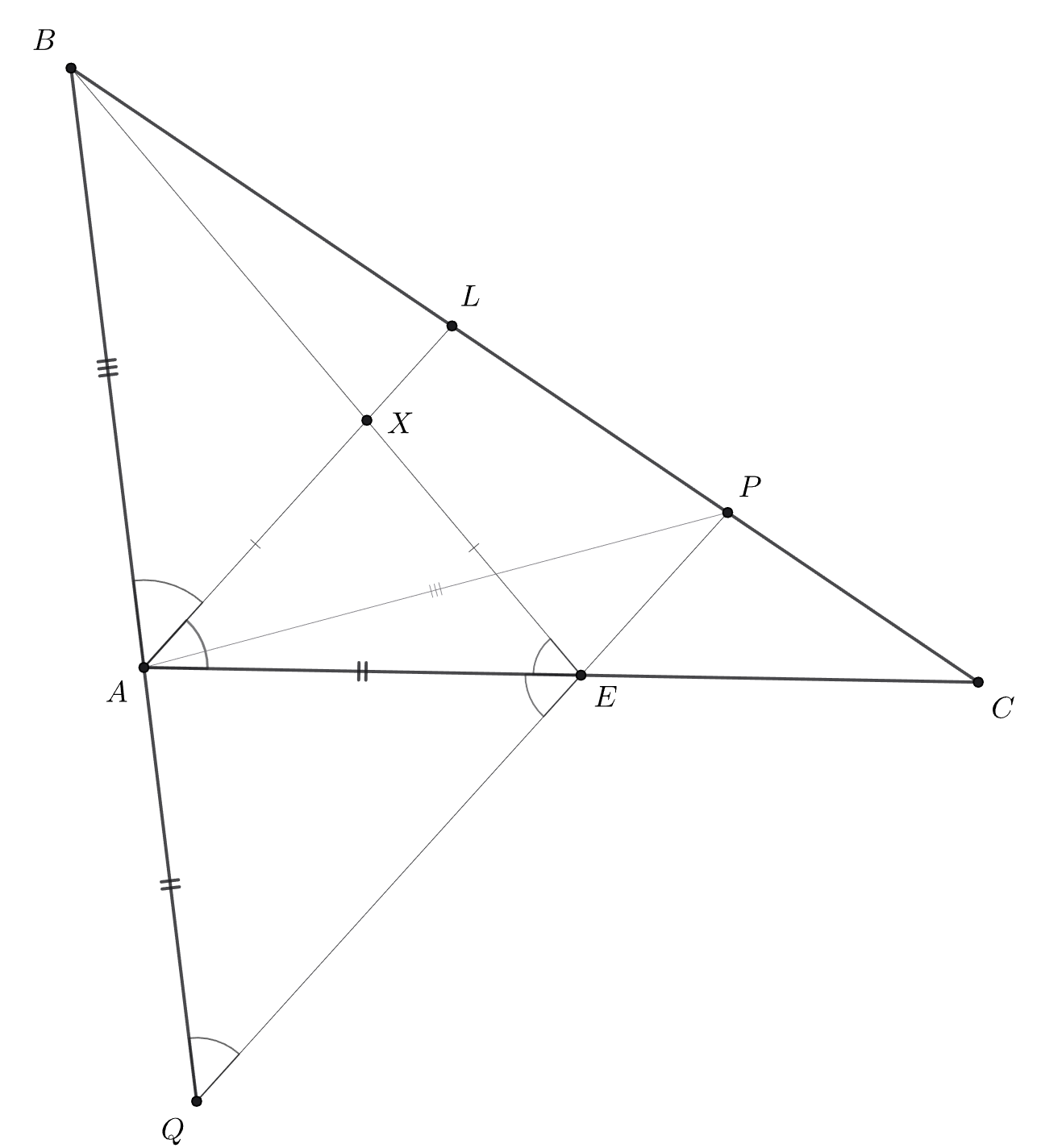
На стороне треугольника
выбрана точка
Биссектриса
пересекает отрезок
в точке
Оказалось, что
и
Чему равно отношение углов
и
треугольника?
Подсказка 1
Чтобы воспользоваться условием AL = BX, нужно сделать некоторое доп. построение, потому что они неудобно расположены.
Подсказка 2
Будет выгодно провести через E прямую параллельно AL, пересечь её с BC и BA в точках P и Q. Тогда мы получим подобные треугольники, в которых фигурируют основные интересующие отрезки.
Подсказка 3
Поищите равнобедренные треугольники на рисунке, также обратите внимание на пару треугольников AQP и AEB.
Пусть прямая, проходящая через точку параллельно
пересекает прямые
и
в точках
и
соответственно. Из
подобия треугольников
и
имеем
откуда В силу параллельности прямых
и
имеем
откуда Кроме того, из равенства
следует, что
откуда
Таким образом, треугольники
и
равны по двум сторонам и углу между ними. Следовательно,
и
откуда и получаем ответ.
Ошибка.
Попробуйте повторить позже
Трапеция с основаниями
и
такова, что угол
— прямой и
. Найдите отношение оснований
.
Подсказка 1
Получается, что сумма двух отрезков равна третьему. Что тогда естественно сделать, чтобы воспользоваться этим условием?
Подсказка 2
Верно, можно попробовать расположить их на одной прямой. Тогда какая фигура после этого получится?
Подсказка 3
Ага, это параллелограмм. Каким же условием мы ещё не воспользовались в задаче? Видим, что накрест лежащие углы у нашего параллелограмма прямые и из построения образовался равнобедренный треугольник. Теперь осталось аккуратно досчитать углы.
Первое решение. Идея — спрямление суммы отрезков в один отрезок с той же длиной.
![]()
На прямой за точку
отметим такую точку
, что
, тогда
, а значит
— параллелограмм.
. Треугольник
— равнобедренный, откуда
. Также из прямоугольного
имеем
,
. То есть
— равнобедренный, значит
, из
чего следует
.
_________________________________________________________________________________________________________________________________________________________________________________
Второе решение. Идея — разбить трапецию на параллелограмм и треугольник (одно из стандартных построений для убийства трапеции).
![]()
Отметим на такую точку
, что
, тогда
— параллелограмм и
. По условию
.
,
а значит,
, откуда
— серединный перпендикуляр к
(потому что
— р/б). Из этого следует, что
-
равнобедренный,
.
,
,
, значит,
— равнобедренный,
то есть
. Таким образом,
.
Ошибка.
Попробуйте повторить позже
Углы при одном из оснований трапеции равны и
, а основания равны
и
. Найдите боковую сторону при угле
.
Подсказка 1
Вспомним, какие у нас бывают дополнительные построения в трапеции. Например, провести сторону параллельно боковой стороне через точку В. Что тогда хорошего можно заметить?
Подсказка 2
Верно, получившаяся фигура - параллелограмм. Тогда параллельные стороны будут равны. Какой ещё факт, связанный с углами, можно заметить из картинки?
Подсказка 3
Ага, равны два угла по 80 градусов. Тогда можно найти третий угол у образовавшегося треугольника. Какой же это будет треугольник?
Проведём через точку прямую
, параллельную
.
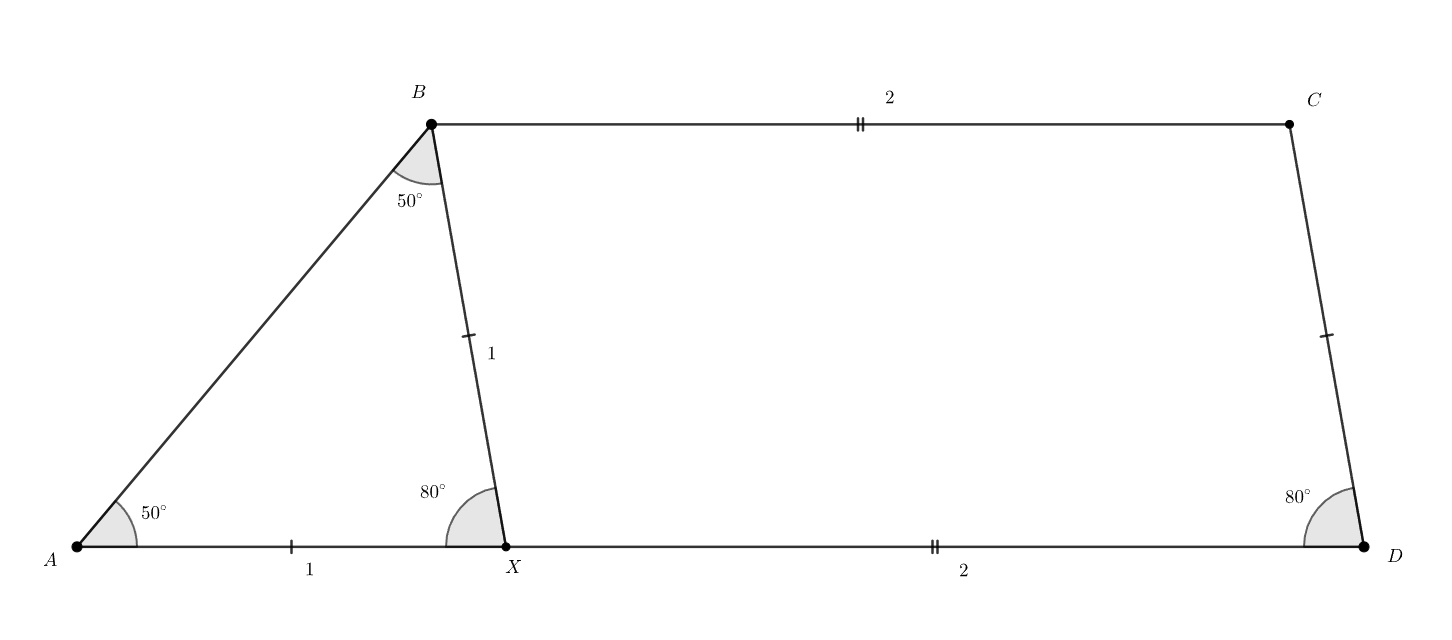
Получили параллелограмм , а значит,
Заметим, что , то есть
— равнобедренный, откуда
Ошибка.
Попробуйте повторить позже
Биссектриса одного угла трапеции делит её боковую сторону пополам. Найдите другую боковую сторону трапеции, если основания трапеции
равны и
.
Подсказка 1
У нас есть биссектриса одного из углов трапеции, и к тому же она является медианой. Какое тогда естественное дополнительное построение можно выполнить?
Подсказка 2
Верно, можно её продлить до пересечения с параллельной стороной. Тогда у нас образуется новый большой треугольник. Попробуем посчитать углы и выяснить что-то о нём.
Подсказка 3
Ага, он равнобедренный. Тогда для решения задачи осталось найти получившееся основание, часть из которого нам известна. Мы ещё не пользовались равенством отрезков. Воспользовавшись ими и равенством углов, попробуйте найти неизвестную часть.
Продлим биссектрису до пересечения с в точке
.
в силу вертикальности и параллельности соответственно, значит и
подобны, притом с коэффициентом 1, откуда
. Осталось заметить, что
— равнобедренный, то есть
Ошибка.
Попробуйте повторить позже
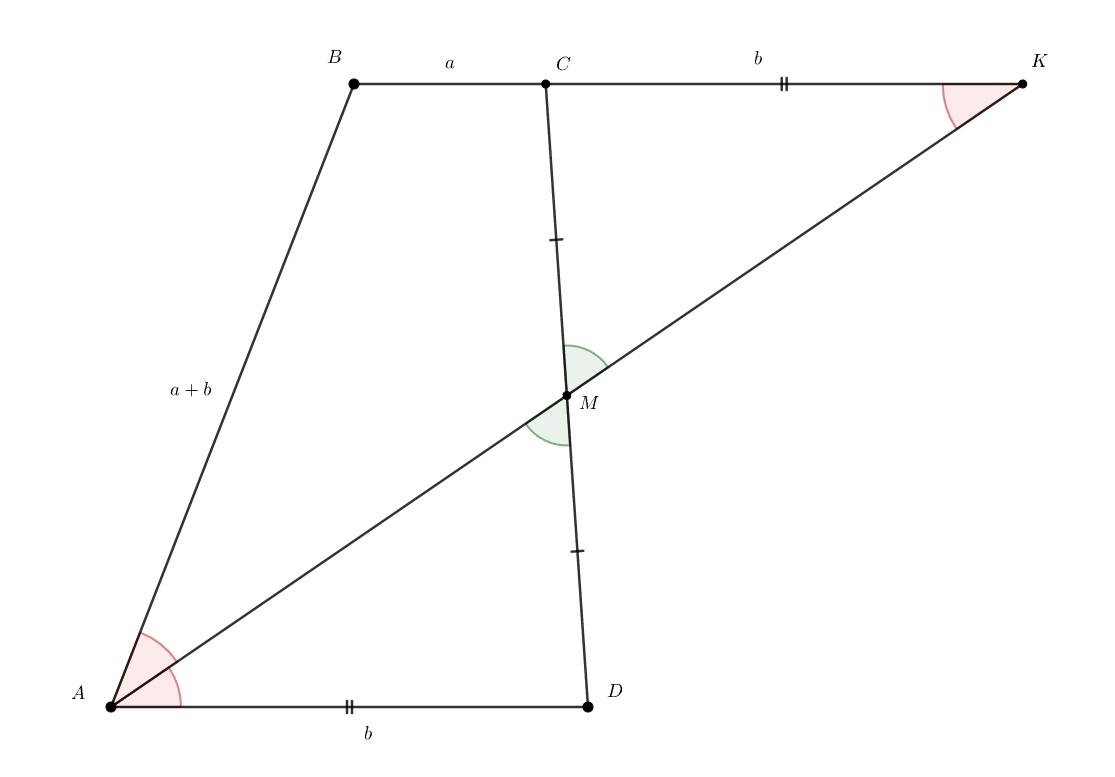
Боковая сторона трапеции равна одному основанию и вдвое меньше другого. Докажите, что вторая боковая сторона перпендикулярна одной из диагоналей.
Подсказка 1
Если нужно доказать перпендикулярность двух отрезков, то имеет смысл подумать о доказательстве через прямоугольный треугольник. Тогда попробуем сделать дополнительное построение, которое поможет нам воспользоваться признаком прямоугольного треугольника.
Подсказка 2
Верно, проведем медиану к большему основанию. Тогда она должна быть вдвое меньше основания. Попробуем понять, какой четырёхугольник у нас получился, используя параллельность оснований трапеции.
Подсказка 3
Ага, получился ромб. Тогда осталось воспользоваться только равенством отрезков.
Пусть — середина
, тогда нетрудно понять, что
— ромб, значит,
. Также по условию
, откуда
.
![]()
Таким образом, — прямоугольный, так как его медиана равна половине стороны, к которой она проведена.
Ошибка.
Попробуйте повторить позже
На продолжении за точку стороны
равностороннего треугольника
выбрана точка
, через неё проведена прямая,
параллельная
. Эта прямая пересекает продолжение стороны
в точке
. Медианы треугольника
пересекаются в точке
. Точка
— середина
. Найдите углы треугольника
Источники:
Подсказка 1
Проведем отрезок АК такой, чтобы АК было параллельно СМ! Заметим, что тогда АКМС это параллелограмм.
Подсказка 2
Давайте заметим, что треугольник BNM правильный, откуда для его центра O: OM = ON ! Тогда мы можем попробовать отметить равные углы и равные отрезки на нашей картинке (их тут много!)
Подсказка 3
Попробуйте доказать, что треугольники KON и COM равны, и, используя, что D - точка пересечения диагоналей параллелограмма, подсчитать углы в треугольнике!
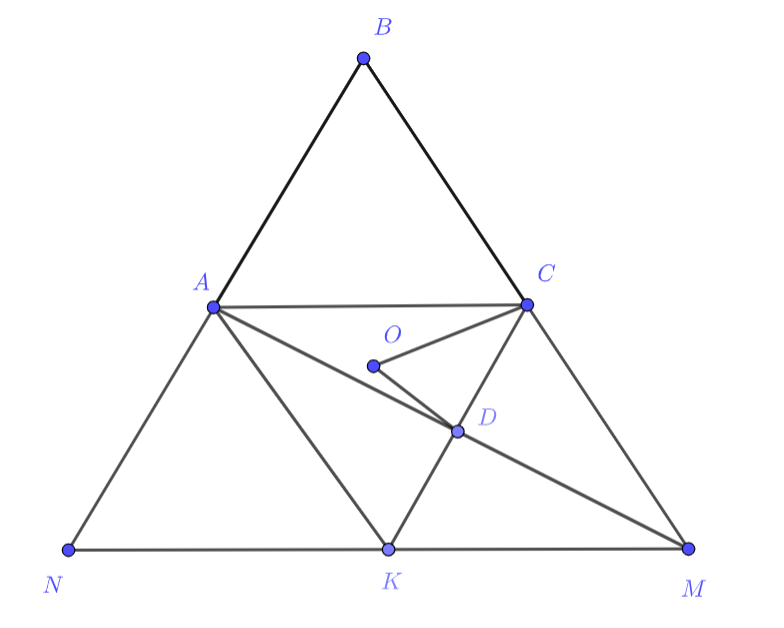
Рассмотрим , откуда
— параллелограмм. Заметим, что
- В
, откуда он равносторонний и
(в силу симметрии).
- Треугольник
правильный, откуда для его центра
:
.
- Аналогично предыдущему
.
Отсюда по двум сторонам и углу между ними , тогда
. Поскольку
является точкой пересечения
диагоналей параллелограмма, то
и
является медианой равнобедренного
. Отсюда
и
снова пользуясь правильностью . В итоге получаем
.



