Гомотетия

Пусть прямая повторно пересекает окружность в точке а прямая повторно пересекает окружность в точке (мы разберём расположение точек, указанное на рисунке; другие случаи рассматриваются аналогично).

Рассмотрим гомотетию с центром переводящую в При такой гомотетии точка переходит в а точка — в Отсюда и

Но и Значит,

Из полученного равенства следует, что точки лежат на одной окружности.

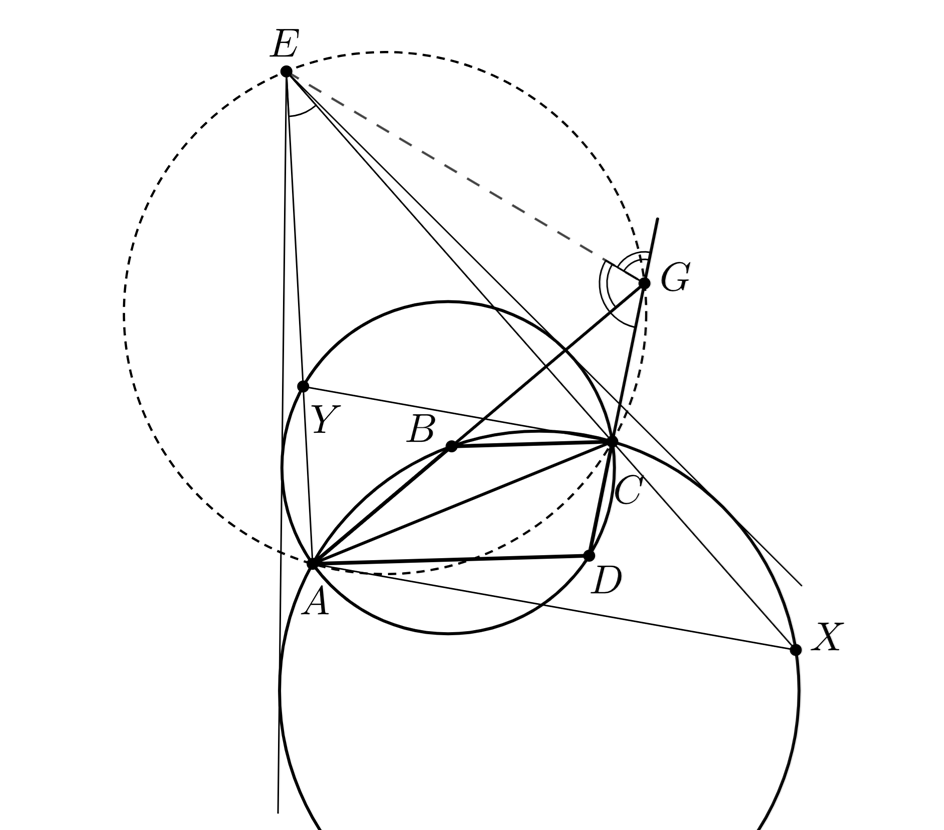
Поскольку точка лежит на серединном перпендикуляре к (т.е. на оси симметрии окружностей и ), она является серединой дуги окружности Значит, лежит на внешней биссектрисе угла

Аналогично показывается, что также лежит на внешней биссектрисе угла

______________________________________________________________________________________________________________________________________________________

Замечание. У задачи есть следующее обобщение. Пусть — четырёхугольник, а — вторая точка пересечения окружностей и (иначе говоря, точка Микеля этого четырёхугольника). Пусть — центр гомотетии с положительным коэффициентом, переводящей в Тогда точки лежат на одной окружности, причём — середина дуги (т.е. — биссектриса угла между и ).

Доказать это можно аналогично решению задачи: имеем (в направленных углах)