Гомотетия
Ошибка.
Попробуйте повторить позже
Четырёхугольник диагоналями разрезан на четыре треугольника. Докажите, что точки пересечения медиан этих треугольников расположены в вершинах некоторого параллелограмма.
Подсказка 1
Как доказать, что четырехугольник является параллелограммом?
Подсказка 2
Достаточно проверить, что противоположные стороны равны и параллельны. Какой инструмент позволяет работать с параллельными отрезками и следить за их отношениями?
Подсказка 3
Гомотетия. Найдите на рисунке отрезок, который бы переходил в противоположные стороны четырехугольника с вершинами в точках пересечения медиан, под действиям гомотетий с одинаковыми коэффициентами.
Подсказка 4
Это диагональ исходного четырехугольника. Что является центрами этих гомотетий? Чему будут равны их коэффициенты?
Подсказка 5
Центры — середины отрезков, между соответствующими вершинами исходного четырехугольника и его точкой пересечениях диагоналей. Коэффициент при этом равен 3.
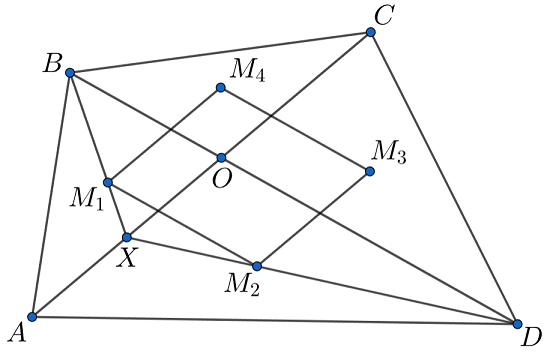
Обозначим центры тяжести треугольников точками Сделаем гомотетию в точке
(середине отрезка
) с
коэффициентом
По свойству точки пересечения медиан точки
и
перейдут в точки
и
соответственно. Значит, прямая
перейдёт в прямую
откуда следует их параллельность. Из аналогичной гомотетии в середине отрезка
следует, что
Таким образом,
Точно так же доказывается параллельность прямых
и
Следовательно,
— параллелограмм, что и требовалось.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




