Турниры в терминах графов и не только (считаем игры и очки)
Ошибка.
Попробуйте повторить позже
команд играют круговой турнир математических боев (каждая играет по одному разу с каждой). За победу дается
очка, за ничью
очко, за поражение —
очков. Команда “Дикие Ёжики” стала единоличным победителем турнира (то есть, она набрала больше очков, чем
любая другая команда). Какое наименьшее количество очков могло у нее оказаться?
Источники:
Решение. Заметим, что всего в турнире сыграно боев, а в каждом бое разыгрывается ровно
очка. Следовательно, сумма очков всех
команд равна
Это означает, что единоличный победитель набрал больше, чем
очков. Действительно, если он набрал
очков
или меньше, то и любая другая команда набрала меньше
очков, тогда сумма всех набранных очков меньше
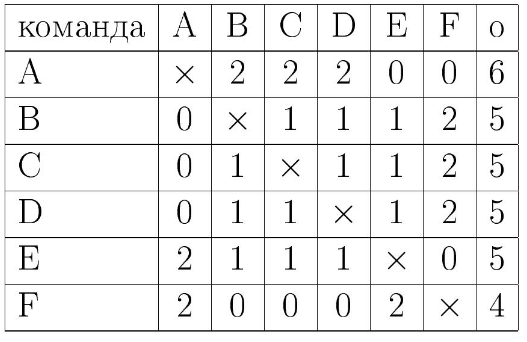
Приведем пример, когда
победитель мог набрать
очков.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




