Лемма о трезубце
Ошибка.
Попробуйте повторить позже
В прямоугольном треугольнике из вершины прямого угла
проведена биссектриса, которая вторично пересекает описанную
окружность треугольника
в точке
Найдите радиус вписанной в треугольник
окружности, если известно, что
, а
Подсказка 1
Середина дуги и центр вписанной окружности явно на что-то намекают... О каких отрезках и точках мы точно можем что-то сказать?
Подсказка 2
Точка I лежит на BW, а еще можно применить лемму о трезубце! Значит, мы можем посчитать BI, а еще мы знаем угол WBK...как тогда найти радиус?
Подсказка 3
Опустим перпендикуляр из I на BA и в прямоугольном треугольнике найдем один из катетов, который и является радиусом. Осталось лишь найти площадь. Т.к. нам известен радиус вписанной окружности, было бы хорошо найти площадь ровно через него. Но для этого нужен полупериметр. Как будем искать?
Подсказка 4
Вспоминаем связь полупериметра и IA (расстояние от центра вписанной окружности до вершины треугольника), IA = p - AC (p - полупериметр), а найти AC несложно, зная WA и WC.
Первое решение.
Пусть — центр вписанной в
окружности. Тогда по лемме о трезубце
Значит,
Пусть — точка касания вписанной окружности стороны
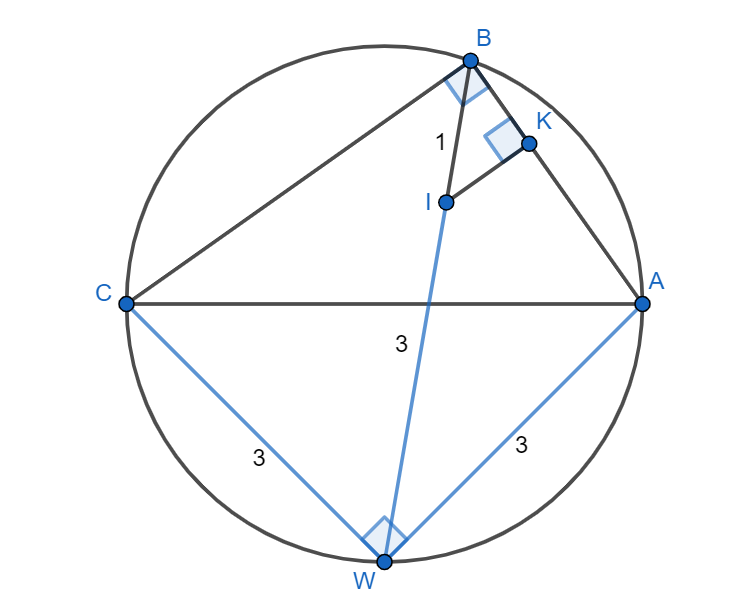
Из прямоугольного треугольника
_________________________________________________________________________________________________________________________________________________________________________________
Второе решение.
как хорды, опирающиеся на равные углы. Из равнобедренного прямоугольного треугольника
находим
По теореме косинусов для треугольников и
стороны
и
являются корнями уравнения
Отсюда, используя формулу разности квадратов, получаем
В итоге
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




