Лемма о трезубце
Ошибка.
Попробуйте повторить позже
Вокруг прямоугольного треугольника с прямым углом
описана окружность, на меньших дугах
и
взяты их середины —
и
соответственно. Отрезок
пересекает катет
в точке
Центр вписанной окружности треугольника
—
Найти
угол
![]()
По лемме о трезубце и
Тогда
— серединный перпендикуляр к отрезку
Т.к.
лежит на
то
Получается, что
— равнобедренный треугольник, причем
Значит, и
Ошибка.
Попробуйте повторить позже
Биссектрисы углов и
треугольника
пересекают описанную окружность этого треугольника в точках
и
соответственно. Прямая, проходящая через центр вписанной окружности треугольника
параллельно стороне
пересекается с прямой
в точке
Докажите, что прямая
касается описанной окружности треугольника
![]()
Пусть — центр вписанной окружности треугольника
По лемме о трезубце
и
Тогда
—
серединный перпендикуляр к отрезку
Т.к.
лежит на
то
Тогда
по трем сторонам.
Следовательно,
Поскольку
по условию, то
Получаем, что
Следовательно,
— касательная к описанной окружности треугольника
Ошибка.
Попробуйте повторить позже
Дана равнобокая трапеция с основаниями
и
В треугольники
и
вписаны окружности с центрами
и
соответственно. Докажите, что прямая
перпендикулярна
Пусть и
— середины дуг
и
описанной окружности трапеции
Ясно, что
Прямые
и
проходят
через точку
По лемме о трезубце
Поскольку
то прямая
— биссектриса
равнобедренного треугольника
Следовательно,
.png)
Ошибка.
Попробуйте повторить позже
Биссектрисы треугольника пересекаются в точке
Касательная в точке
к описанной окружности треугольника
пересекает стороны
и
в точках
и
соответственно. Докажите, что
.
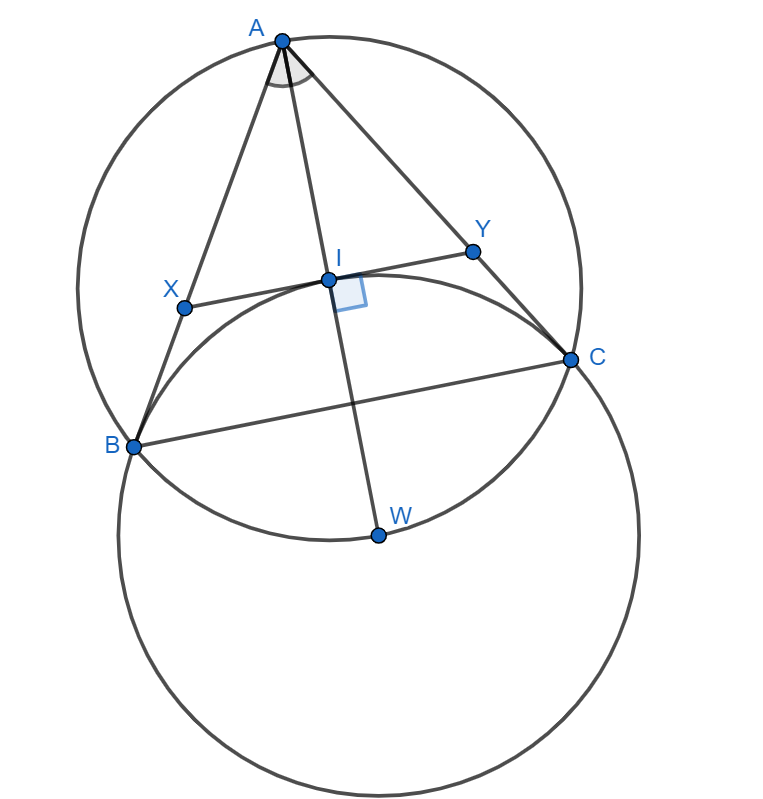
Пусть вторая точка пересечения
с описанной окружностью
Биссектриса
является высотой из леммы о трезубце, потому
что на биссектрисе лежит радиус
проведённый в точку касания
Ошибка.
Попробуйте повторить позже
Около треугольника описана окружность. Хорды, соединяющие середину дуги
с серединами дуг
и
, пересекает
стороны
и
в точках
и
соответственно. Докажите, что точки
,
и центр вписанной в треугольник
окружности
лежат на одной прямой.
Источники:
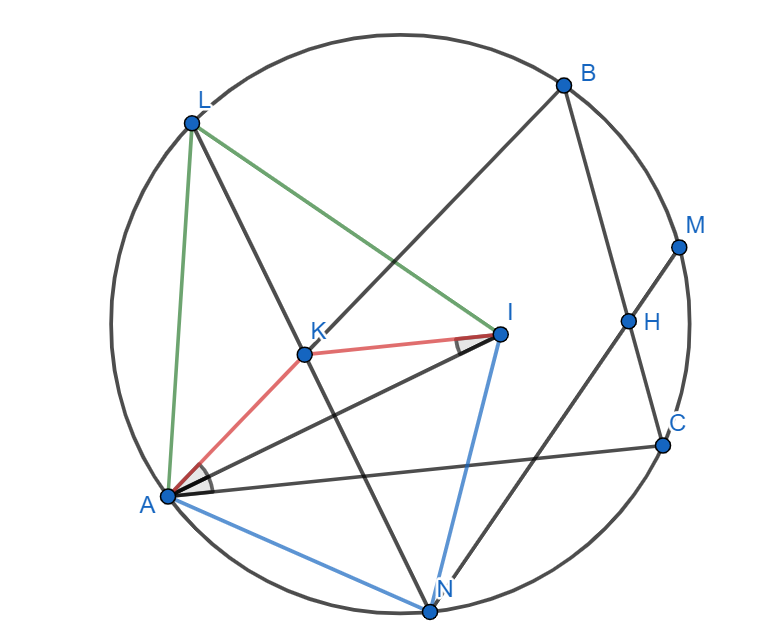
Обозначим за середины дуг за
соответсвенно, а также пусть
центр вписанной окружности треугольника
Тогда, по лемме о трезубце имеем:
Значит, — серединный перпендикуляр к отрезку
Отсюда следует, что
Теперь немного посчитаем углы. В силу
равенства
получим:
Вспомним, что
- биссектриса угла
Тогда
В итоге,
имеем:
Аналогично доказывается, что Но так как через одну точку, не лежащей на заданной прямой, можно провести только одну
прямую, параллельную данной, то точки
лежат на одной прямой.
Ошибка.
Попробуйте повторить позже
В прямоугольном треугольнике из вершины прямого угла
проведена биссектриса, которая вторично пересекает описанную
окружность треугольника
в точке
Найдите радиус вписанной в треугольник
окружности, если известно, что
, а
Первое решение.
Пусть — центр вписанной в
окружности. Тогда по лемме о трезубце
Значит,
Пусть — точка касания вписанной окружности стороны
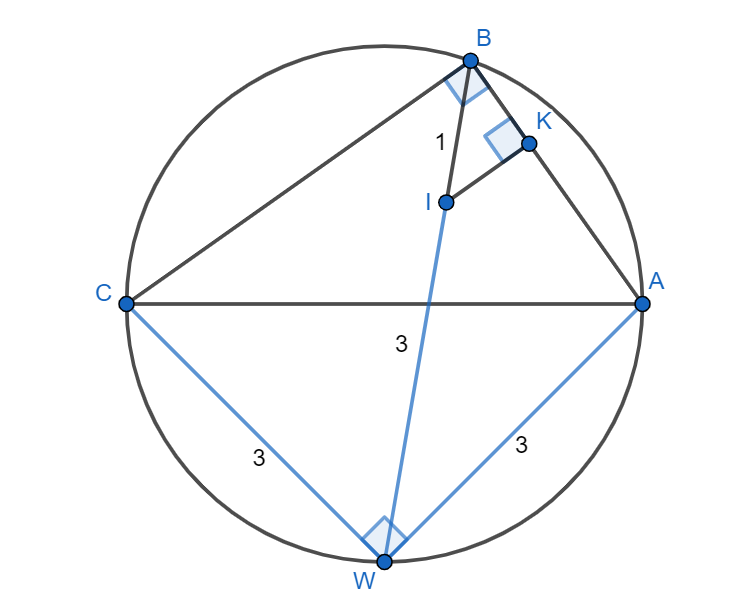
Из прямоугольного треугольника
_________________________________________________________________________________________________________________________________________________________________________________
Второе решение.
как хорды, опирающиеся на равные углы. Из равнобедренного прямоугольного треугольника
находим
По теореме косинусов для треугольников и
стороны
и
являются корнями уравнения
Отсюда, используя формулу разности квадратов, получаем
В итоге
Ошибка.
Попробуйте повторить позже
Пусть радиусы описанной и вписанной окружностей треугольника равны
и
соответственно.
а) Прямая вторично пересекает описанную окружность треугольника
в точке
. Докажите, что
б) Докажите, что квадрат расстояния между центрами вписанной и описанной окружностей равен [Формула
Эйлера]
в) Докажите, что радиус описанной около треугольника окружности всегда не меньше, чем диаметр вписанной в данный треугольник окружности. А когда достигается равенство?
Решение пункта (а)
![]()
Пусть Из условия следует, что
— биссектриса угла
, то есть
Поэтому . По лемме о трезубце
Пусть — проекция точки
на
. Из прямоугольного треугольника
находим, что
Итого
Решение пункта (б)
![]()
Переписав формулу в виде , докажем, что обе ее части равны произведению
, где
— точка пересечения
биссектрисы угла
с описанной окружностью.
Пусть — точки пересечения прямой, содержащей
и окружности, описанной около треугольника
По свойству пересекающихся хорд
И по доказанному ранее в пункте (а) , поэтому
Первый вариант решения пункта (в)
По формуле Эйлера
Так как правая часть неотрицательна, то и левая часть неотрицательна, то есть
Получаем, что , то есть радиус описанной окружности всегда не меньше диаметра вписанной окружности.
Равенство достигается тогда и только тогда, когда
То есть центр вписанной окружности совпадает с центром описанной окружности. Это означает, что биссектрисы являются серединными перпендикулярами. Так как это выполняется для любой вершины треугольника, то каждая пара сторон треугольника является парой равных сторон. То есть треугольник является равносторонним.
Второй вариант решения пункта (в)
![]()
Пусть и
— вписанная и описанная окружности треугольника
. Через каждую вершину этого треугольника проведём
прямые, параллельные противолежащим сторонам. Получим треугольник
, подобный данному с коэффициентом
. Пусть
—
радиус вписанной окружности треугольника
.
Опишем около окружности треугольник
, стороны которого соответственно параллельны сторонам треугольника
так, что прямая
и точка
расположены по разные стороны от прямой
, прямая
и точка
— по разные стороны от
прямой
, прямая
и точка
— по разные стороны от прямой
Треугольник подобен треугольнику
и, следовательно, треугольнику
. Стороны треугольника
не
меньше соответствующих сторон треугольника
(второй из этих треугольников целиком заключён внутри первого). Поэтому
Равенство достигается только в случае, когда все стороны треугольника касаются окружности
. Тогда
Следовательно, То же верно для остальных углов. Треугольник является правильным.
Третий вариант решения пункта (в)
Пусть и
— стороны треугольника,
— полупериметр,
— площадь. Тогда
Положим
Имеем
Где последнее — в силу неравенства о средних для трёх чисел.
Следовательно, . Равенство достигается, когда
, то есть
в случае равностороннего треугольника.
Ошибка.
Попробуйте повторить позже
Вписанная окружность треугольника касается сторон
и
в точках
и
соответственно. Точка
— центр вневписанной
окружности, касающейся стороны
Точки
и
— середины
и
Прямые
и
пересекаются в точке
Докажите, что
лежит на описанной окружности треугольника
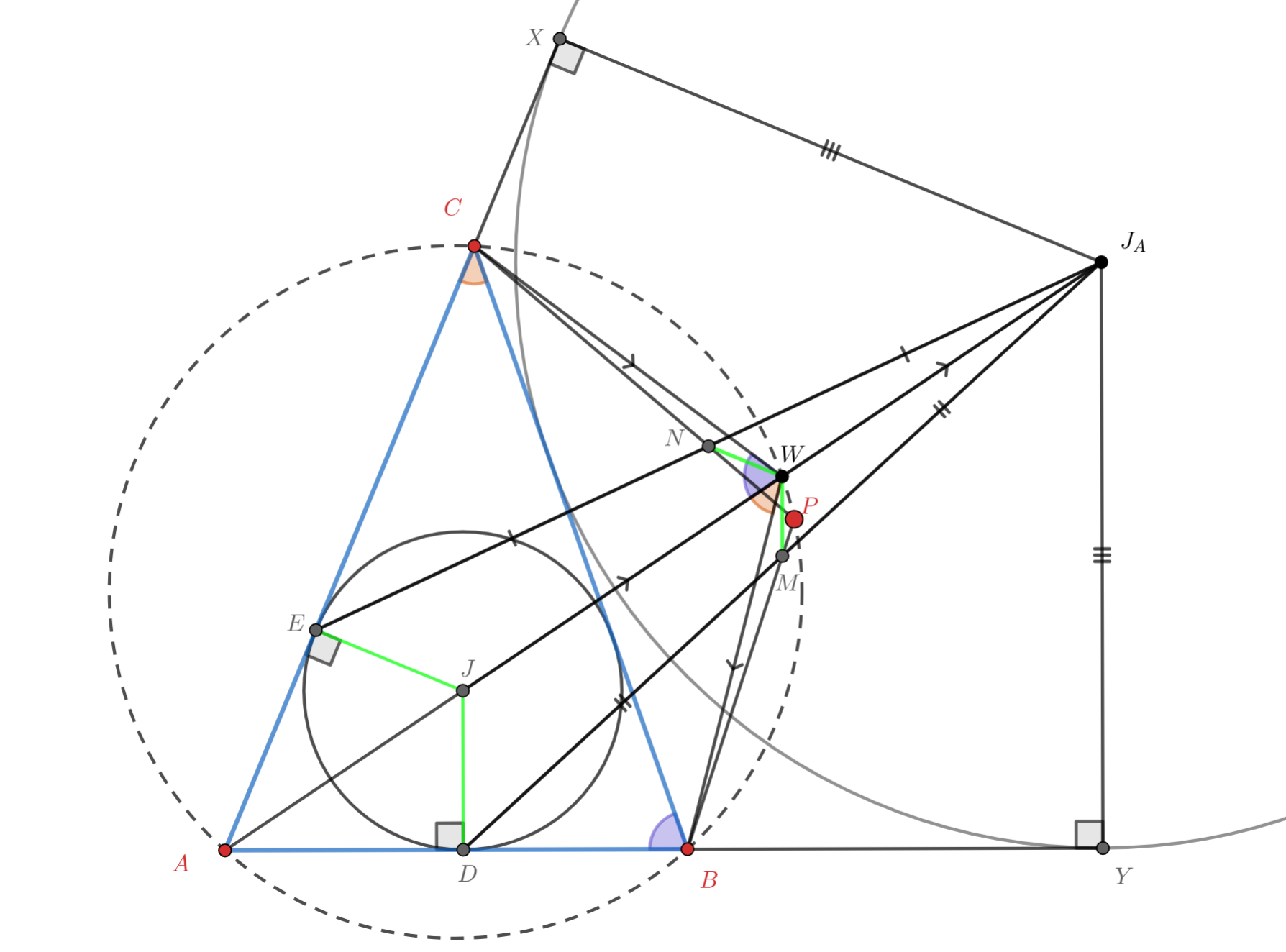
Пусть и
— центры вписанной и вневписанной окружностей
соответственно, a
— точка пересечения описанной
окружности
с биссектрисой
. Тогда по лемме о трезубце
. Проведем радиусы
и
.
Рассмотрим
и
.
и
являются средними линиями этих треугольников соответственно (так как
и
по условию). Так как
(как радиусы), то и
Пусть
Посчитаем .
Посчитаем .
Отсюда получается, что — вписанный
лежит на описанной
окружности
Ошибка.
Попробуйте повторить позже
Отрезок, соединяющий середины “меньших” дуг и
описанной окружности треугольника
пересекает стороны
и
в
точках
и
Докажите, что
— ромб, где
— центр вписанной в треугольник
окружности.
Пусть и
– середины “меньших” дуг
и
Согласно лемме о трезубце,
и
являются равнобедренными
треугольниками с вершинами в
и
соответственно. Значит треугольники
и
равны по трем сторонам, и
прямая
является биссектрисой в треугольниках
и
Тогда она же является перпендикуляром и медианой, а
значит
является серединным перпендикуляром к
Рассмотрим треугольник
Прямая
в нем является
биссектрисой, а также, по доказанному, содержит высоту. Значит треугольник
равнобедренный,
а так
как
и
лежат на серединном перпендикуляре к
то
откуда
действительно ромб.
![]()
Ошибка.
Попробуйте повторить позже
В неравнобедренном треугольнике точка
— середина стороны
— точка пересечения медиан,
— центр вписанной
окружности. Известно, что
. Докажите, что
.
Источники:
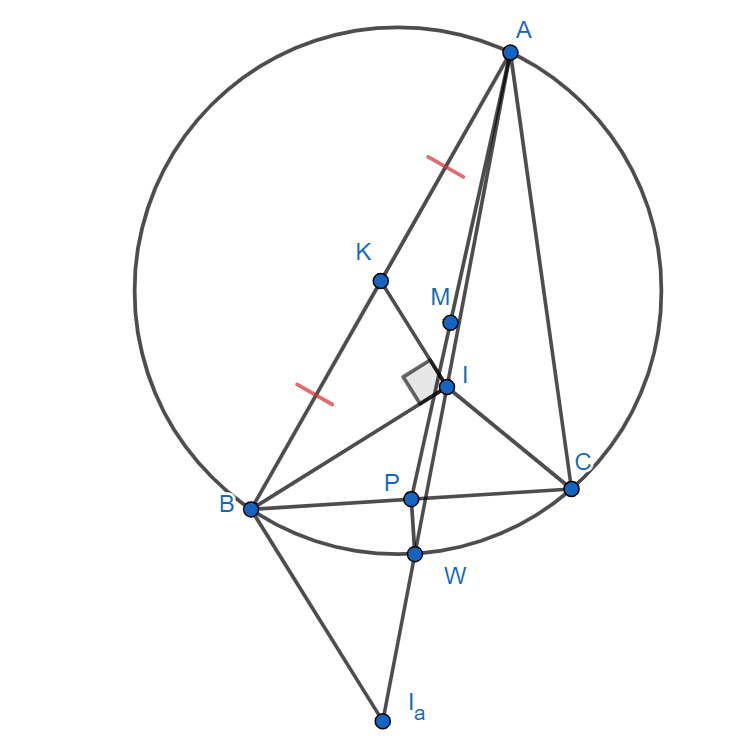
Давайте поймем, как реализовать странное условие про угол. Вспомним про то, что внутренняя и внешняя биссектрисы одно и того же угла
перпендикулярны. Тогда давайте дополнительно отметим центр вневписанной окружности данного треугольника, касающейся стороны
Пусть это
Значит,
Так как то
— средняя линия треугольника
По лемме о трезубце
— середина
следовательно,
Тогда
Пусть — середина стороны
Тогда по свойству медианы:
Тогда
Так как — середина дуги
не содержащей
то
А это означает требуемое.
Ошибка.
Попробуйте повторить позже
Биссектрисы треугольника пересекаются в точке
, внешние биссектрисы его углов
и
пересекаются в точке
. Окружность
с центром в точке
проходит через точку
и касается прямой
в точке
Окружность
с центром в точке
проходит
через точку
и касается прямой
в точке
Отрезки
и
пересекаются в точке
Найдите отношение
.
Источники:
Первое решение.
Проведём в окружности диаметр
, а в окружности
диаметр
. Заметим, что
, поскольку
внутренняя и внешняя биссектриса угла перпендикулярны. Следовательно, точка
лежит на
, а точка
- на
.
![]()
Кроме того, , поскольку
касается
в точке
, поэтому
. Аналогично,
. Итого, четырёхугольник
- параллелограмм, пусть его диагонали пересекаются в точке
. Тогда
, а отрезок
- средняя линия
треугольника
, поэтому точка
середина отрезка
. Таким образом,
, откуда следует, что
.
_________________________________________________________________________________________________________________________________________________________________________________
Второе решение.
Обозначим через середину дуги
описанной окружности
треугольника
, а через
середину другой
её дуги
. Пусть луч
вторично пересекает
в точке
. Поскольку
- диаметр окружности
, то
.
По лемме о трезубце — середина отрезка
. Поскольку
и
, то
Продлим луч до пересечения с
в точке
.
![]()
Так как внешний для треугольника
, а также четырёхугольник
- вписанный, мы получаем, что
, поэтому окружность
касается прямой
в точке
. Также эта
окружность проходит через
, следовательно, это и есть окружность
. Аналогично, окружность
описана около треугольника
.
Значит, IP - общая хорда окружностей и
, а тогда
серединный перпендикуляр к отрезку
. Поскольку к тому же
, мы получаем, что
проходит через середину отрезка
, то есть
, а тогда
.
Ошибка.
Попробуйте повторить позже
Олег и Оливер гоняют на велосипедах с одинаковыми угловыми скоростями: Оливер — по круговой траектории а Олег — по круговой
траектории
в два раза меньшего радиуса, причем они стартуют с двух ближайших точек окружностей и круг Олега
лежит внутри круга Оливера. По окружности
также движутся два помощника, поддерживающих экран (т.е. хорду с
концами в точках, в которых расположены помощники) так, что расстояние от каждого из них до Олега всегда такое же, как
и расстояние от Олега до Оливера. Докажите, что на протяжении всей гонки экран касается некоторой фиксированной
окружности.
Источники:
Обозначим за и
Олега, Оливера и двух помощников соответственно, за
— центр положительной гомотетии окружностей
и
Из условия следует, что прямая
всегда проходит через
причем, так как радиусы окружностей отличаются в два раза,
отрезок
делится точкой
пополам. Отметим точку
— пересечение луча
с
Поскольку равные хорды стягивают
равные меньшие дуги, точка
— середина дуги
то есть прямая
содержит внутреннюю биссектрису треугольника
а еще
По лемме о трезубце это означает, что точка
является центром вписанной окружности треугольника
обозначим эту окружность за

Покажем, что является искомой окружностью. Она касается отрезка
в силу построения, поэтому достаточно проверить, что она
не зависит от времени. Как показано выше, центр
— это
обозначим ее радиус за
. Также обозначим за
расстояние между
центрами
и
а за
— постоянный радиус
Посчитаем степень точки относительно
двумя способами:
Величины и
не зависят от времени, поэтому
также от него не зависит, следовательно, окружность
имеет постоянный центр
и радиус, что и требовалось доказать.
Ошибка.
Попробуйте повторить позже
В окружность вписан четырёхугольник Отметили центры окружностей, вписанных в треугольники
Докажите, что отмеченные точки являются вершинами прямоугольника.
Первое решение.
Отметим точки — середины дуг
Точка
лежит на биссектрисе
угла
аналогично точка
лежит на прямой
Заметим, что
так как они стягивают одну дугу.
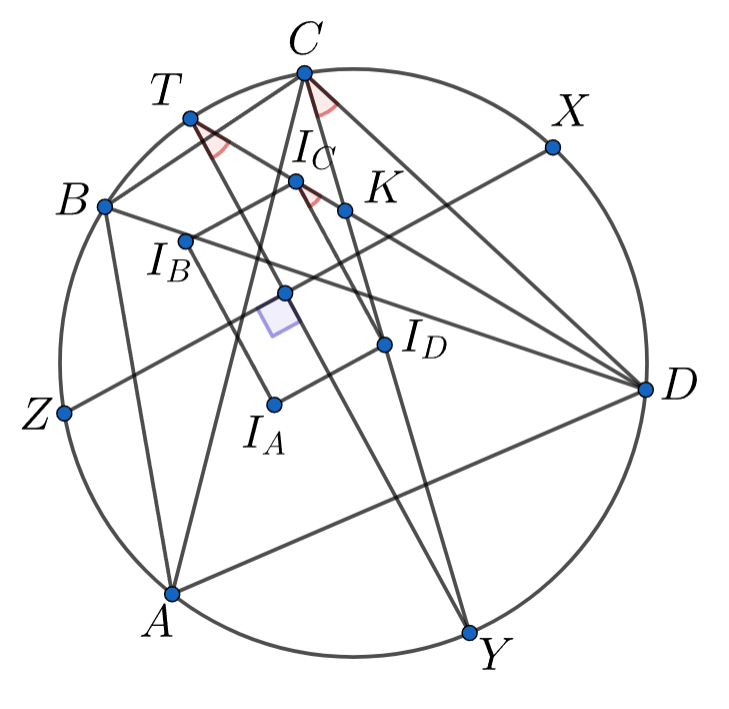
По лемме о трезубце так что
— вписанный. Значит,
Следовательно, Аналогично
То есть
Точно так же доказывается параллельность
и
Таким образом,
— параллелограмм.
Теперь покажем, что он прямоугольник. В силу вышедоказанных параллельностей для этого достаточно доказать, что А это
следует из того, что угол между
и
равен полусумме высекаемых ими дуг
и
а она как раз равна
______________________________________________________________________________________________________________________________________________________
Второе решение.
Если в треугольнике точка
является центром вписанной окружности, то
.
![]()
По лемме
Значит, лежат на одной окружности. Аналогично,
лежат на одной окружности. Значит,
Аналогично можно доказать, что остальные углы четырехугольника равны
, и значит,
—
прямоугольник.
_________________________________________________________________________________________________________________________________________________________________________________
Замечание.
Предложенный факт широко известен в узких олимпиадных кругах под названием Японская теорема о вписанном четырёхугольнике. Но в задаче без доказательства пользоваться им нельзя, потому что суть задачи в том, чтобы доказать этот факт. А вот леммой про угол между биссектрисами на олимпиаде пользоваться можно без доказательства.
Ошибка.
Попробуйте повторить позже
Биссектрисы углов и
треугольника
пересекают его описанную окружность в точках
и
соответственно и пересекают
друг друга в точке
Окружности
и
с центрами
и
касаются отрезков
и
соответственно. Докажите, что через
точку
можно провести прямую, касающуюся обеих окружностей
и
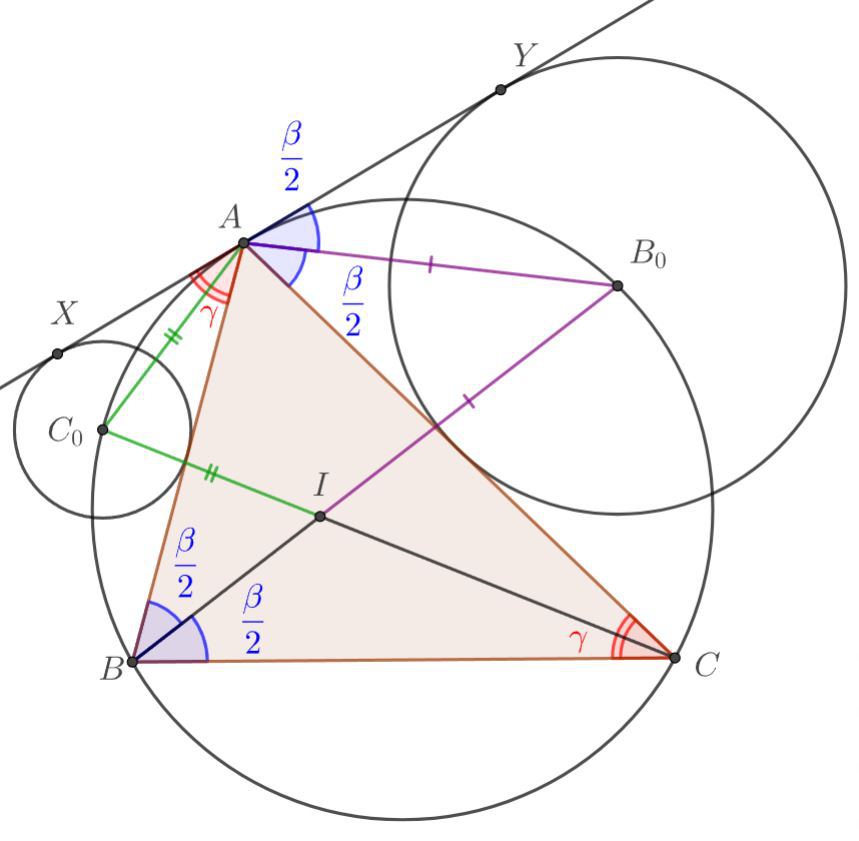
Обозначим углы треугольника через Проведём из
касательные
и
к окружностям. Заметим, что
Нетрудно понять, что
— биссектриса угла
то есть
Следовательно,
Аналогично
Значит,
Таким образом,
— внешняя общая касательная двух окружностей.
Осталось заметить, что по лемме о трезубце
и
то есть точки
и
симметричны относительно
Сделаем
симметрию относительно
Касательная
перейдёт во вторую общую внешнюю касательную
а точка
— в точку
значит
лежит на
что и требовалось.
Ошибка.
Попробуйте повторить позже
Точки и
— центры описанной и вписанной окружностей соответственно для треугольника
,
— середина
дуги
описанной окружности (не содержащей точки
). Известно, что
и
Найдите
Источники:
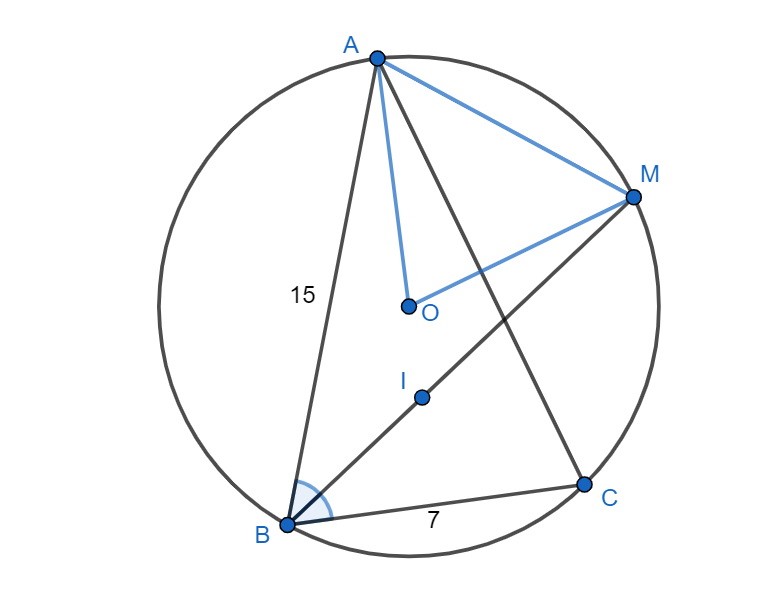
Середина дуги лежит на биссектрисе
По лемме о трезубце (по условию
).
Отсюда
По теореме косинусов
Ошибка.
Попробуйте повторить позже
Постройте треугольник по центру описанной окружности , центру вписанной окружности
и вершине
.
Заметим, что раз мы знаем центр описанной окружности и ее радиус , то мы можем провести описанную окружность. Проведем
прямую
до пересечения с описанной окружностью. Получим точку
. По лемме о трезубце мы знаем, что
. Значит,
если мы проведем окружность с центром в
и радиусом
, то она пересечет описанную окружность в 2 точках:
и
, так как эти
точки лежат и на описанной окружности, и на данной.
![]()
Ошибка.
Попробуйте повторить позже
В треугольнике — середина
— середина дуги
описанной окружности треугольника. Докажите, что углы
и
равны.
![]()
Продлим прямую до пересечения с описанной окружностью (
здесь центр вписанной окружности). Назовем точку пересечения
Заметим, что точки
(центр описанной окружности),
и
(так как это середина дуги
) лежат на серединном перпендикуляре
к
Значит точки
и
лежат на одной прямой и
диаметр.
Значит, Нам нужно доказать, что углы
и
равны. Заметим, что
а
Значит, нам
достаточно показать, что углы
и
равны.
Внимательно посмотрим на эти углы и заметим, что то, что эти углы равны равносильно тому, что треугольник и
подобны,
а это равносильно тому, что
или тому, что
Итак, нам осталось доказать это равенство. Треугольник прямоугольный с высотой
отсюда
а
по лемме о трезубце. Значит,
Ошибка.
Попробуйте повторить позже
В треугольнике построена точка
, симметричная центру
вписанной окружности относительно центра
описанной
окружности. Докажите, что
где – радиус описанной окружности треугольника
Источники:
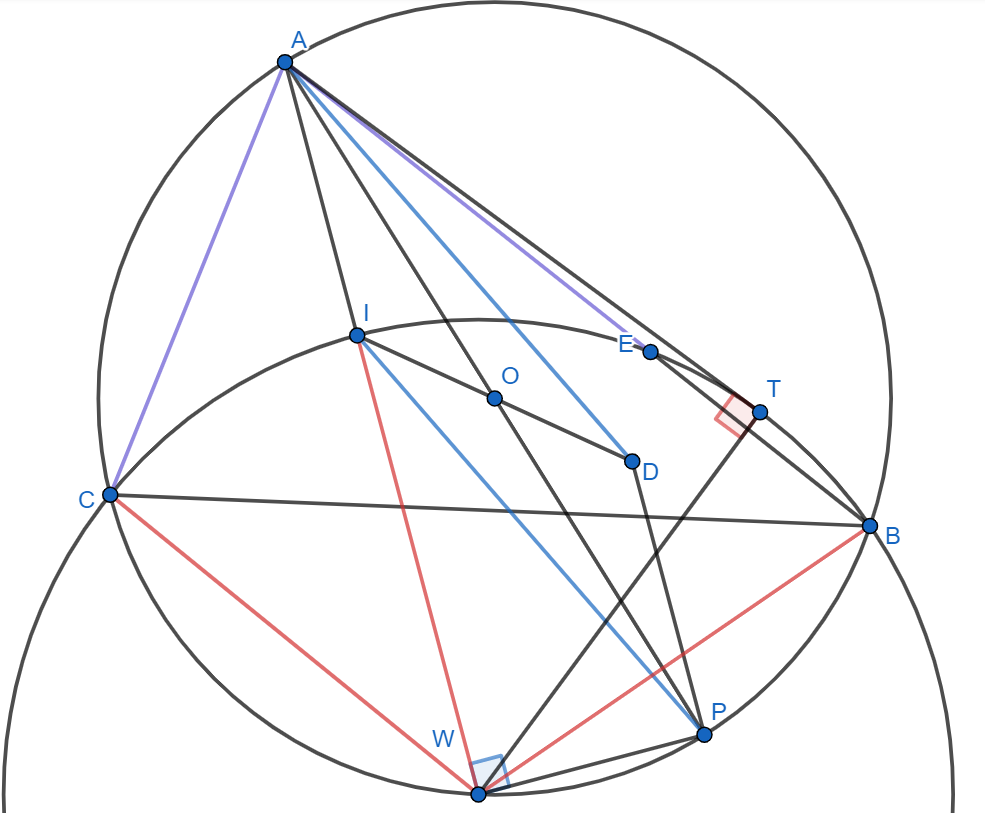
Пусть биссектриса пересекает описанную окружность в точке
. Проведем диаметр
. Тогда
- параллелограмм и
.
Тогда доказываемое равенство можно записать в виде:
Кроме того, так как - диаметр окружности, то угол
- прямой. Тогда правую часть равенства (1) можно
преобразовать:
Таким образом, задача сводится к доказательству равенства
Воспользуемся известным фактом: , который называют теоремой трилистника или леммой о трезубце. Центр
описанной окружности треугольника BIC лежит на биссектрисе угла
, поэтому точки пересечения этой окружности со сторонами
угла
попарно симметричны относительно биссектрисы
. В частности, симметричны точки
и
, значит,
.
Пусть - касательная к описанной окружности треугольника ВIC. Тогда
Из треугольника по теореме Пифагора
Из равенств (3) и (4), учитывая также, что , получим:
то есть равенство (2), которое равносильно утверждению задачи.
В заключительной части решения можно обойтись без теоремы Пифагора, если использовать степень точки
относительно
окружности
Это утверждение, равно как и теорему о трилистнике, школьники могут использовать без доказательства.
Ошибка.
Попробуйте повторить позже
Точки и
лежат на окружности с центром в точке
Луч
вторично пересекает описанную около треугольника
окружность в точке
причём точка
оказалась внутри этой окружности. Докажите, что
— биссектриса угла
Источники:
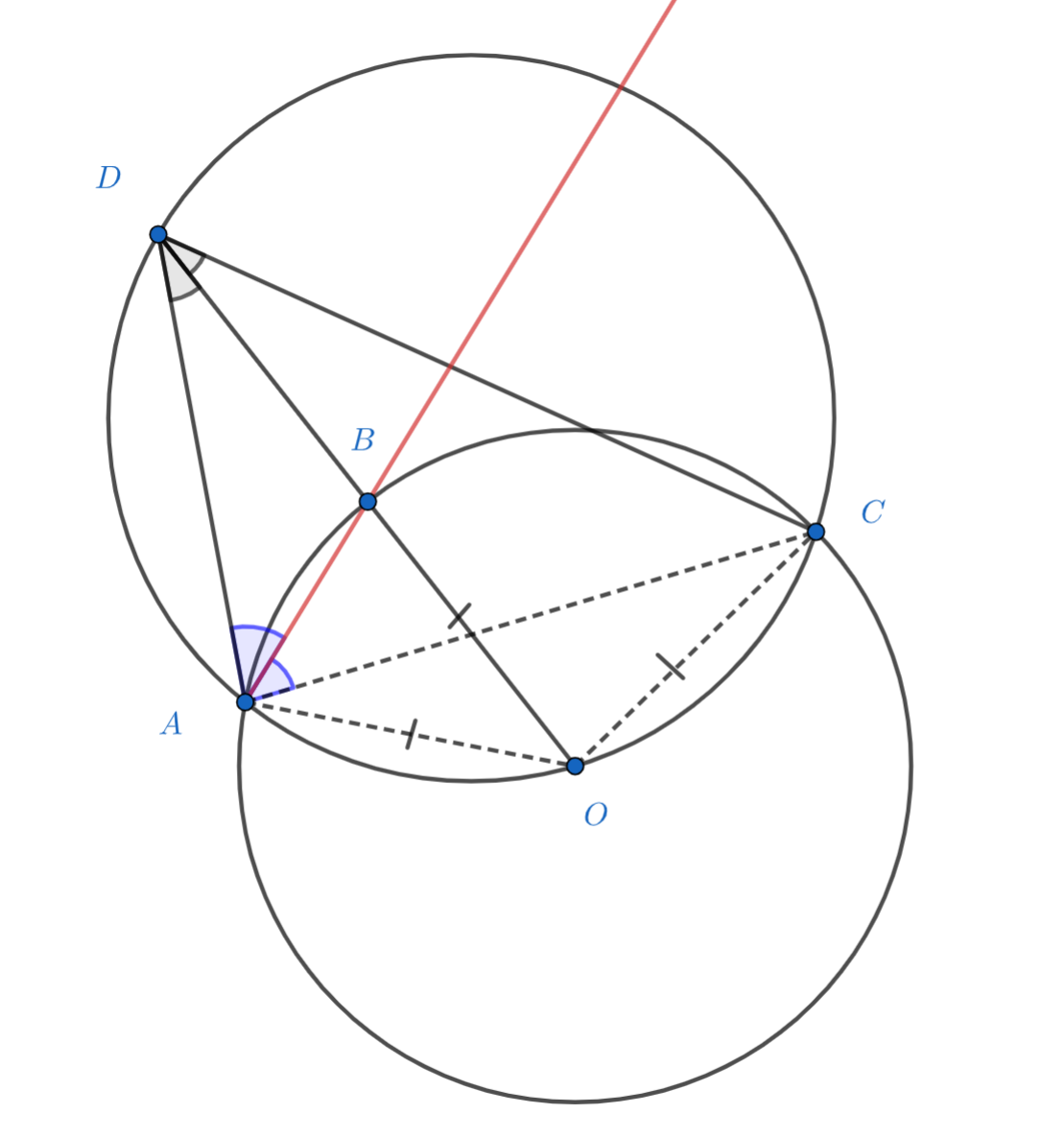
Рассмотрим окружность, на которой лежат точки и
Точка
равноудалена от точек
и
поэтому является серединой
дуги
Значит,
— биссектриса угла
в треугольнике
Точка лежит на луче
и находится на том же расстоянии от точки
что точки
и
поэтому по лемме о трезубце
является центром вписанной в треугольник
окружности, а значит,
тоже биссектриса.
Ошибка.
Попробуйте повторить позже
В неравнобедренном треугольнике проведена биссектриса
Точка
— центр вписанной окружности треугольника
Серединный перпендикуляр к отрезку
пересекает окружность, описанную около треугольника
в точках
и
Точка
на отрезке
выбрана так, что
Докажите, что точки
и
лежат на одной
окружности.
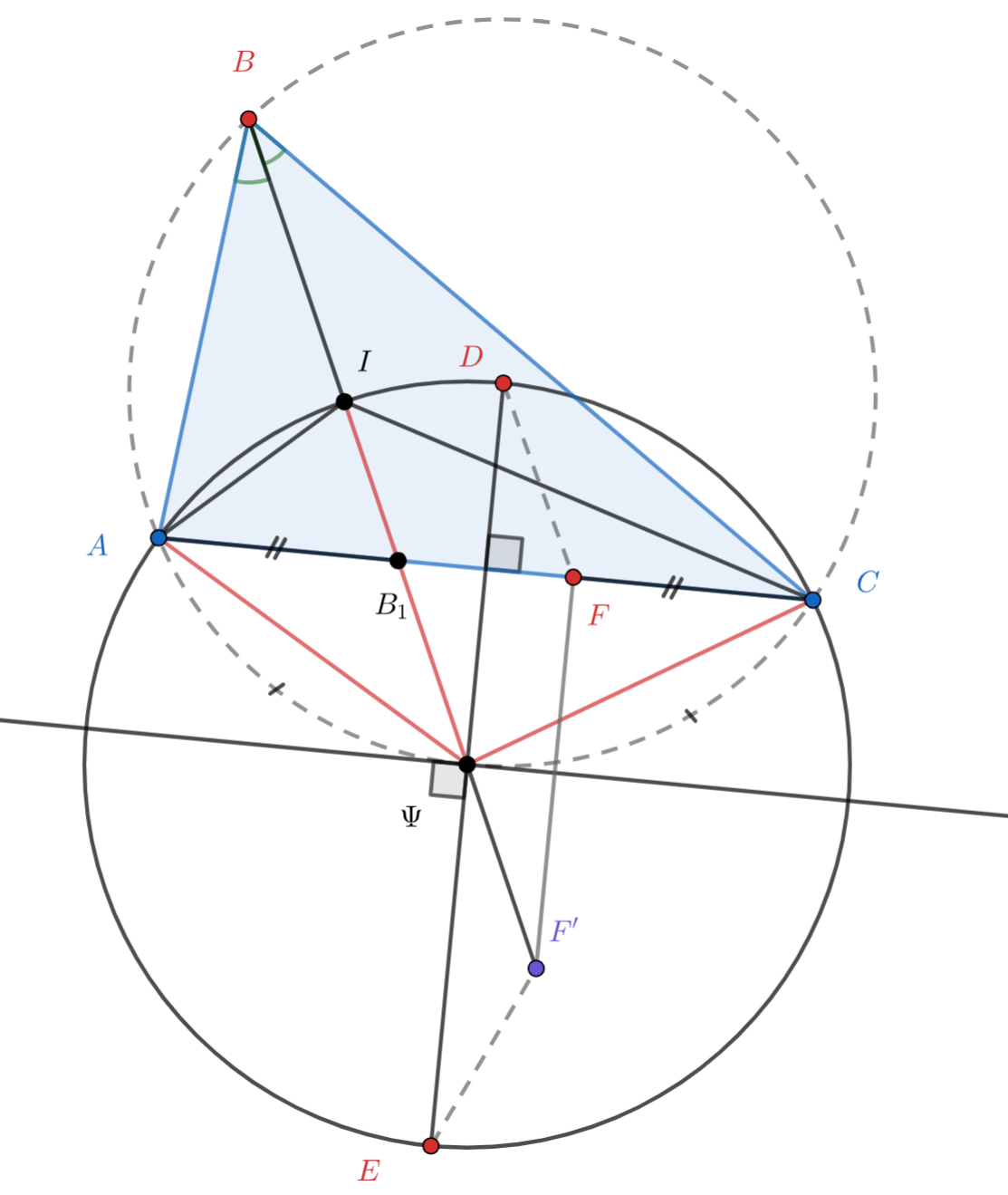
Обозначим через середину дуги описанной окружности треугольника
, не содержащей точку
. Тогда
лежит на
прямой
. Кроме того, по лемме о трезубце точка
равноудалена от точек
и
, поэтому
является центром
описанной окружности треугольника
и
лежит на отрезке
. Пусть точка
симметрична точке
относительно
серединного перпендикуляра к
. Очевидно,
— равнобедренная трапеция, значит,
лежат на одной
окружности.
Докажем, что точка лежит на этой же окружности. Заметим, что точка
лежит на
, поскольку
равноудалена от точек
и
, т.е.
— диаметр окружности с центром
и радиусом
. Из подобия треугольников
и
следует, что
, что равносильно равенству
Из последнего равенства следует, что точки лежат на одной окружности.



