Лемма о трезубце
Ошибка.
Попробуйте повторить позже
В неравнобедренном треугольнике проведена биссектриса
Точка
— центр вписанной окружности треугольника
Серединный перпендикуляр к отрезку
пересекает окружность, описанную около треугольника
в точках
и
Точка
на отрезке
выбрана так, что
Докажите, что точки
и
лежат на одной
окружности.
Подсказка 1
У нас есть треугольник AIC и его описанная окружность. Может, мы знаем что-то хорошее про ее центр?
Подсказка 2
По лемме о трезубце, это середина дуги AC! Обозначим ее за O. Кроме того, он лежит на отрезке ED, т.к. это серединный перпендикуляр к AC. Как можно теперь связать точки E и D так, чтобы можно было что-то сделать с точкой F похожим образом?
Подсказка 3
Например, можно сказать, что E и D симметричны относительно прямой, перпендикулярной ED и проходящей через O) Давайте также отразим F относительно этой прямой, и получим точку F'. Что мы получили?
Подсказка 4
Мы получили, что есть DEFF' - вписанная равнобокая трапеция. Мы хотим доказать, что E, D, B, F на одной окружности, а уже есть DEFF'..Как можно переформулировать теперь задачу?
Подсказка 5
Можно теперь доказывать, что точки F', D, B и E лежат на одной окружности) Для этого попробуйте доказать, что O - центр окружности B₁FF'! Это можно сделать с помощью симметрии, чтобы доказать, что O лежит на B₁F') А дальше как действовать?
Подсказка 6
А дальше можно воспользоваться подобием треугольников OAB и OAB₁ и записать отношения сторон) После с помощью предыдущей подсказки можно по-другому выразить это равенство отношений, и получится требуемое условие для того, чтобы F', D, B и E лежали на одной окружности)
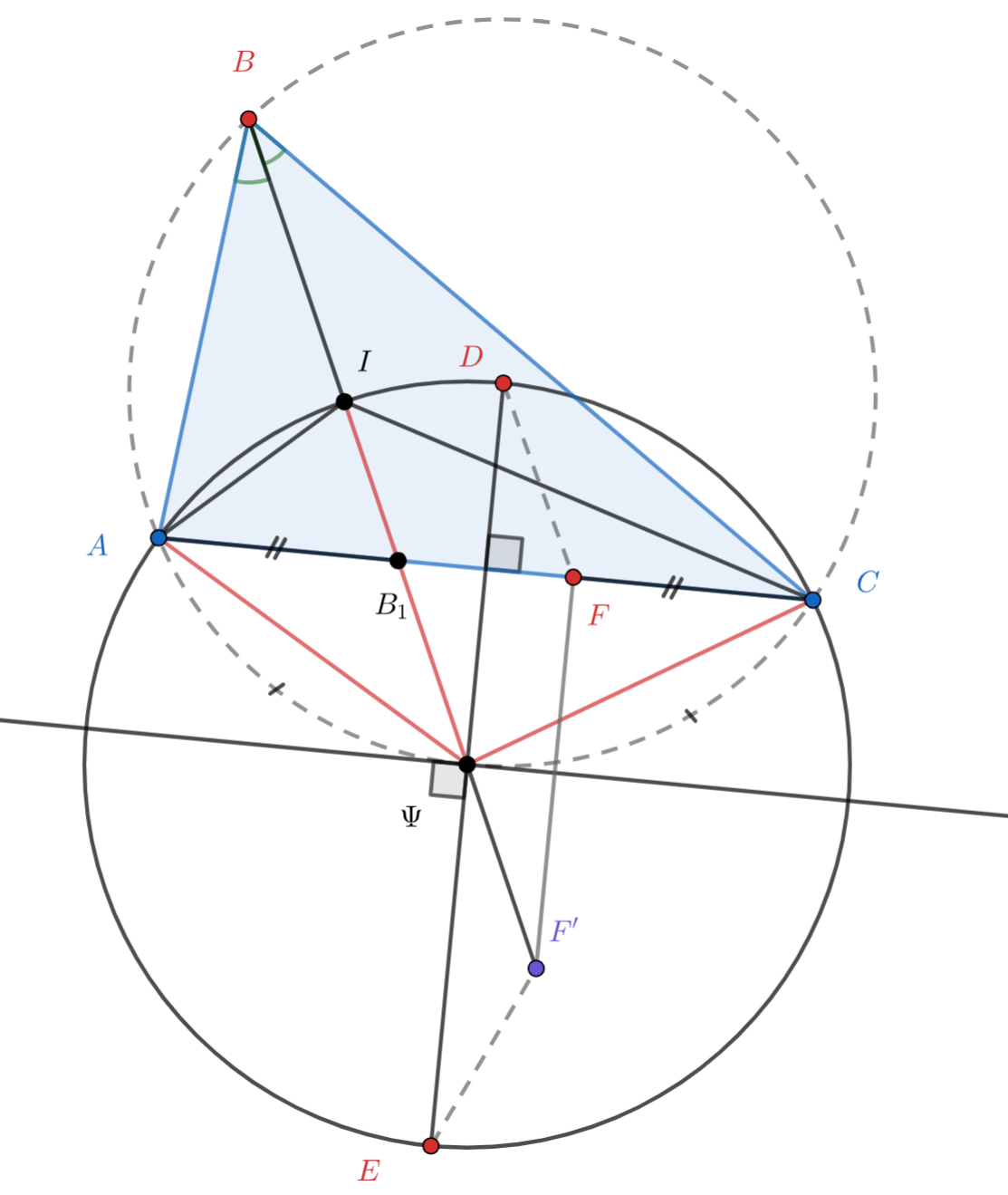
Обозначим через середину дуги описанной окружности треугольника
, не содержащей точку
. Тогда
лежит на
прямой
. Кроме того, по лемме о трезубце точка
равноудалена от точек
и
, поэтому
является центром
описанной окружности треугольника
и
лежит на отрезке
. Пусть точка
симметрична точке
относительно
серединного перпендикуляра к
. Очевидно,
— равнобедренная трапеция, значит,
лежат на одной
окружности.
Докажем, что точка лежит на этой же окружности. Заметим, что точка
лежит на
, поскольку
равноудалена от точек
и
, т.е.
— диаметр окружности с центром
и радиусом
. Из подобия треугольников
и
следует, что
, что равносильно равенству
Из последнего равенства следует, что точки лежат на одной окружности.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




