Длины векторов и скалярное произведение
Ошибка.
Попробуйте повторить позже
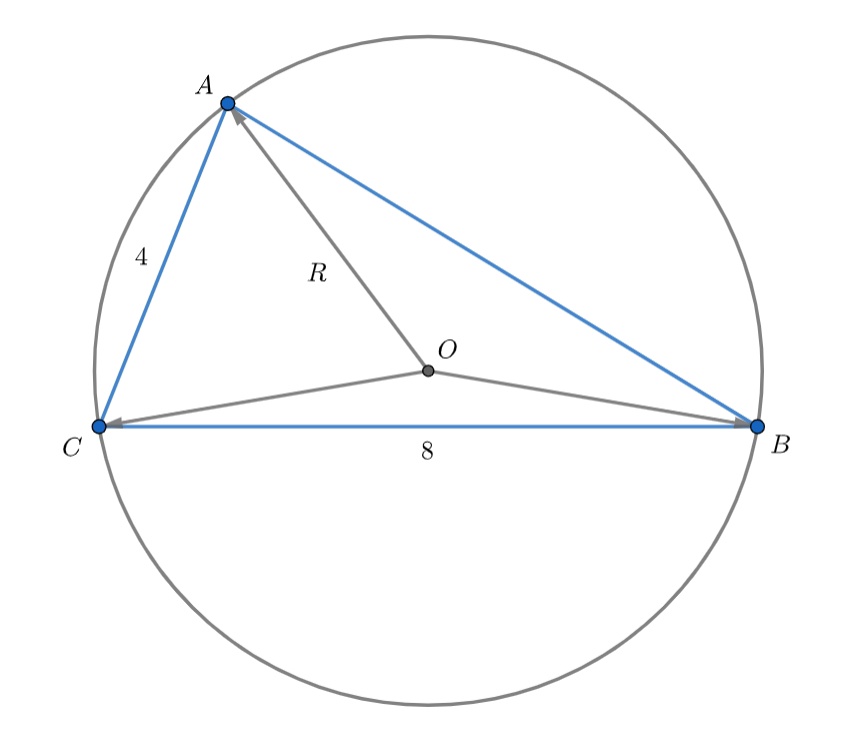
Точка является центром окружности, описанной около треугольника
со сторонами
и
. Найдите длину стороны
, если длина вектора
равна
.
Подсказка 1
В таких задачах на счет нужно очень четко понять, какие переменные мы вводим и зачем это делать. Какие переменные у нас уже известны? Две стороны треугольника. Значит, если попробовать выразить наше выражение векторное, через часть из известных переменных и того, что нам нужно найти, то может что-то получится.
Подсказка 2
Давайте выразим каждый из векторов в выражении через векторы CA и AB, тогда выходит, что |3AC + AB| = 10 (здесь написаны векторы). Далее, нам ничего не остается как возводить в квадрат, но там вылезет косинус из произведения векторов. Как побороть эту проблему, если у нас в виде переменных остаются AB и cos(BAC).
Подсказка 3
Конечно, у нас есть cos(BAC) и AB, значит все намекает на теорему косинусов для треугольника ABC и стороны BC. Вычтя из нашего равенства, которое получилось возведением в квадрат модуля, равенство из теоремы косинусов, получим уравнение, в котором есть AB*cos(BAC), приравненное к константе. Что тогда можно сделать, чтобы найти AB?
Подсказка 4
Само собой, остается подставить это в уравнение, полученное из модуля, так как после подстановки, там останется одна неизвестная - AB, а значит, задача решена!
Будем пользоваться тем, что скалярный квадрат вектора равен квадрату длины вектора.
Из условия получаем, что
А теперь возведём обе части в квадрат:
По теореме косинусов из треугольника имеем
Вычитая это равенства из полученного выше, получаем
С учётом имеем
Подставим в
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




