Длины векторов и скалярное произведение

Первое решение

Без ограничений общности будем считать, что указанный отрезок соединяет середины сторон и Введем вектора таким образом, что

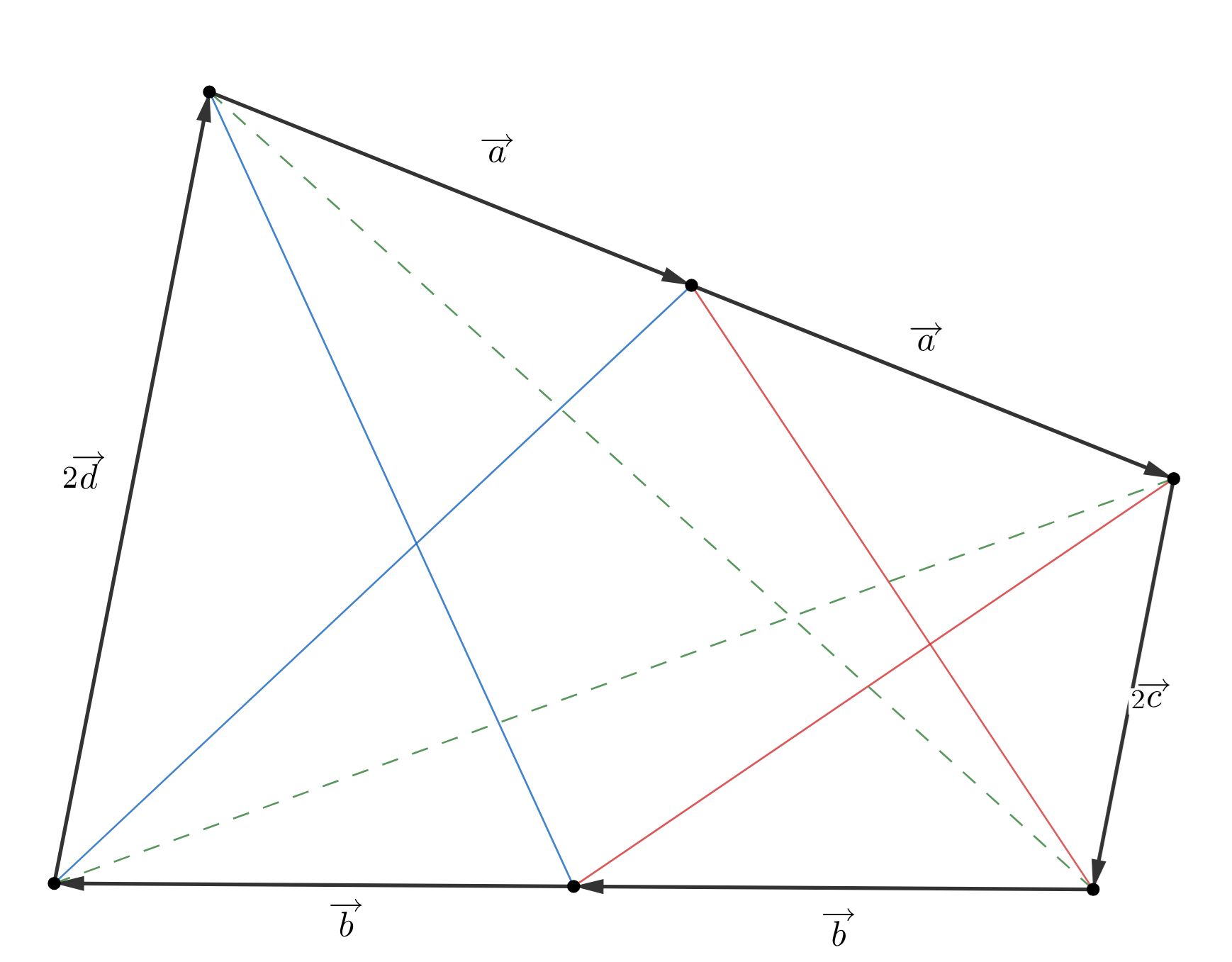
Поскольку диагонали образованных четырехугольников равны имеют место равенства

Здесь и далее, для любых двух векторов Таким образом, вычитая второе равенство из первого, получим

Поскольку имеем

следовательно, диагонали исходного четырехугольника так же равны.

_________________________________________________________________________________________________________________________________________________________________________________

Второе решение

Пусть и — середины сторон соответственно и четырёхугольника Из признака равенства треугольников по двум сторонам и медиане, проведённой к третьей следует равенство треугольников и поэтому а значит, Треугольники и равны по трём сторонам, поэтому Тогда

Тогда треугольники и равны по двум сторонам и углу между ними, следовательно,