Тема Векторы и координаты в планиметрии

Длины векторов и скалярное произведение

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела векторы и координаты в планиметрии

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#79601

Векторы $⃗a ,⃗a,⃗a ,⃗a 1 2 3 4$ , расположенные в одной плоскости с вектором $⃗b$ , имеют равную длину, отличную от длины вектора $⃗b$ . Известно, что

−→ || || 9⃗a1− 4⃗a2− 5⃗b= 16⃗a3− 9⃗a4− 7⃗b= 0 ,|⃗a1− ⃗b|= 8

Найдите $|| ⃗|| |⃗a3− b|.$

Источники: ОММО - 2024, задача 4 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Давайте выразим всё через a₁ и a₃, ведь именно они выделяются: a₁ = 4/9 * a₂ + 5/9 * b, a₃ = 9/16 * a₄ + 7/16 * b. Что мы можем заметить здесь? А если вспомнить словосочетание «отношение отрезков»?

Подсказка 2

Это похоже на то, что мы взяли вектора a₂ и b, провели их от одной точки и на отрезке, который соединяет их концы, поставили точку с отношение 7/9, и вот этот вектор равен a₁. Аналогично с a_3. Как теперь можно наше наблюдение совместить с фактом про равные длины из условия?

Подсказка 3

Давайте создадим треугольник AOE, где OA = a₂, OE = b. Тогда вектор a₁ понятно находится по рассуждению выше. Но ведь у нас еще есть a₃. Пусть тогда OD = a₄. Тогда, опять же, a₃ понятно ищется на картинке. Но что же все таки с равными длинами? В какой конструкции у нас много точек на одном расстоянии лежит?

Подсказка 4

Верно! Концы векторов a₁, a₂, a₃, a₄ лежат на одной окружности, при этом прямые DC, AB, OE пересекаются в одной точке и делятся понятным отношением этой самой окружностью. Что тогда остается сказать, если даны окружность и отношения секущих?

Подсказка 5

Можно сказать, что у нас EB * EA = EC * ED, если BA = 4x, а EC = 9y, то y = x/2. Осталось воспользоваться условием задачи ещё раз

Показать ответ и решение

Выразим $⃗a = 4a⃗+ 5⃗b 1 92 9$ и $⃗a = 9-⃗a +-7⃗b 3 164 16$ . Поэтому $⃗a 1$ — чевиана в треугольнике $AOE$ со сторонами $OA = ⃗a 2$ и $OE =⃗b$ , которая делит третью сторону $AE$ в отношении $5$ к $4$ . А $a⃗3$ — чевиана треугольника $OED$ со сторонами $⃗ OE =b$ и $OD = ⃗a4$ , делящая $ED$ в отношении $9$ к $7$ . Так как векторы $⃗a1,⃗a2,⃗a3,⃗a4$ равны, то они лежат на окружности с центром в точке $O$ , а треугольники $AOB$ и $OCD$ — равнобедренные.

$PIC$

По теореме об отрезках секущих

4x ⋅9x= 9y⋅16y

Откуда

y = x 2

По условию $4x= 8$ , следовательно $|a⃗3− ⃗b|= 9y = 9.$

Ответ: 9

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#82783

Старинный подземный ход имеет свод параболической формы (то есть в поперечном сечении туннель ограничен полом — осью $Ox$ и графиком некоторой параболы $2 y = a− bx$ ). Ширина туннеля (измеряется по полу) равна $24$ , высота туннеля равна $18$ . Ход укрепили распорками — на параболе отметили точки $A$ , $B$ , $C$ , $D$ и соединили их между собой балками. Балки $AB$ и $CD$ параллельны полу, $AD$ пересекается с $BC$ , и при этом $∘ ∠ACB = ∠ADB = 90$ . Найдите расстояние между балками $AB$ и $CD$ .

Источники: Ломоносов - 2024, 11.6 (см. olymp.msu.ru)

Подсказки к задаче

Подсказка 1

Давайте введем на нашей картинке систему координат, которая была бы нам удобна. К примеру симметричную относительно прямой симметрии параболы и нулевой высоты в тоннеле. Тогда, что нужно чтобы зафиксировать картинку? Каких параметров будет достаточно, чтобы выразить через это всю картинку?

Подсказка 2

Нам достаточно h - высоты вершины, а также длины основания - 2l(для симметрии). Тогда, если наша парабола задается функцией f(x) = a - bx^2, то f(l) = f(-l), f(0) = h. Тогда f(x) = h(1 - x^2/l^2). Значит, мы можем задать две точки A и C, а остальные - будут отличаться от симметричных только умножением на -1 абсциссы. Давайте так и сделаем - пусть x_1 - абсцисса А, а x_2 - абсцисса C. Тогда как нам выразить перпендикулярность, если мы работаем в координатах? Мы ведь не использовали еще ни разу тот факт, что, к примеру, AC и CB перпендикулярны.

Подсказка 3

Верно, мы можем выразить это через скалярное произведение векторов AC и CB. После того, как мы запишем и преобразуем выражение, у нас получится, что -(x_2^2 - x_1^2) - (h^2)/(l^4) * (x_2^2 - x_1^2)^2 = 0. Но при этом, у нас x_1 != x_2, поэтому x_2^2 - x_1^2 = - (h^2)/(l^4). Тогда, нам остается понять, чему равно расстояние между балками и записать ответ!

Показать ответ и решение

Обозначим ширину тоннеля за $2l$ , а высоту за $h$ . Из этих параметров однозначно выводятся параметры параболы: $x$ принадлежит отрезку $[−l,l],$ а $y(l)= y(−l)= 0,$ так что

hx2 y(x)= h− -l2-

Теперь зададим координаты точек так:

2 2 2 2 A = (x1,h(1− xl12 )),B = (−x1,h(1 − x1l2 )),C = (x2,h(1 − x2l2 )),D = (x2,h(1− x2l2 ))

Так как $AB$ и $CD$ параллельны полу, то понятно, что ординаты $A$ и $B$ одинаковы. Значит, абсциссы отличаются только знаком. Аналогично для $C$ и $D$ .

$PIC$

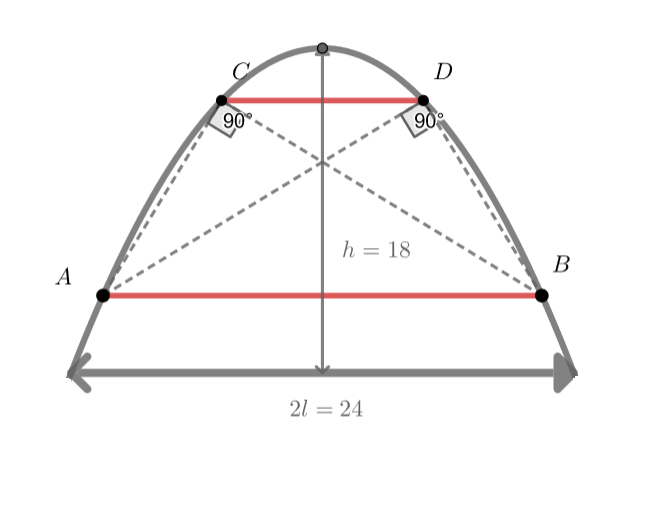
Тогда перпендикулярность $AC$ и $CB,$ $AD$ и $DB$ можно выразить, например, через равенство нулю скалярных произведений. Достаточно рассмотреть одну пару, так как рисунок симметричен.

AC = (x2− x1; h(x2− x2),CB = (−x1 − x2; h(x2− x2)) l2 1 2 l2 2 1

2 2 h2- 2 22 AC ⋅CB =− (x2− x1)− l4 (x2− x1)= 0

Тогда либо $2 2 (x2− x1) =0$ (но балки не совпадают, поэтому такой вариант не подойдет), либо

2 2 l4 (x2− x1)= − h2

А расстояние между балками это:

2 |hl2(x22− x21)|= lh-= 8

Ответ: 8

Ошибка.
Попробуйте повторить позже

Задача 3#97371

(a) Докажите, что сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.

(b) Докажите, что сумма квадратов сторон произвольного четырехугольника не меньше, чем сумма квадратов его диагоналей, причем равенство достигается только в случае параллелограмма.

Подсказки к задаче

Подсказка, пункт а

Введите векторы, образующие стороны параллелограмма. Честно напишите через эти 2 вектора сумму квадратов длин диагоналей и сумму квадратов длин всех четырех сторон.

Подсказка 1, пункт б

Введите векторы, образующие стороны четырехугольника, их получится 4. Как проверять то, что требуется в задаче? Нужно выразить все выражения через наши 4 вектора. Как понять, что равенство получается только в случае параллелограмма?

Подсказка 2, пункт б

Если перед вами параллелограмм, то противоположные векторы должны быть равны с обратным знаком, причем это равносильно. Подумайте, как это можно написать, и сведите задачу к этим двум выражениям.

Показать доказательство

(a) Пусть $v1,v2$ — векторы, образованные сторонами параллелограмма. Тогда диагонали параллелограмма образованы векторами $v1 +v2$ и $v1 − v2.$ Наконец, в силу билинейности скалярного произведения

2 2 (v1+v2) +(v1− v2) = (v1+ v2,v1+ v2)+ (v1− v2,v1− v2)=

2 2 =((v1,v1)+2(v1,v2)+(v2,v2)+((v1,v1)− 2(v1,v2)+ (v2,v2))= 2(v1 + v2)

(b) Пусть $v1,v2,v3,v4$ — векторы, образованные сторонами четырехугольника. Тогда векторы, образованные диагоналями четырехугольника, могут быть выражены как $v1+ v2,v2+ v3,v3+ v4,v4+v1.$ Тогда доказываемое неравенство можно представить в виде

(v + v − v − v )2 (v − v − v + v )2 v21 + v22 + v23 +v24 ≥-1--22-3---4 + -1---22-3---4

После раскрытия скобок в правой части, имеем

( ) ∑4 1 ∑4 i=1(vi,vi)≥ 4 2i=1(vi,vi)− 4(v1,v3)− 4(v2,v4)

4∑ (v,v)+ 2(v ,v )+ 2(v ,v )≥ 0 i=1 i i 1 3 2 4

(v1+ v3,v1+ v3)+ (v2 +v4,v2+ v4)≥0

(v1+ v3)2+ (v2 +v4)2 ≥0

последнее верно при любых $v1,v2,v3,v4,$ причем равенство достигается тогда и только тогда, когда $v1 = −v3,v2 =− v4,$ то есть когда исходный четырехугольник является параллелограмом.

Ошибка.
Попробуйте повторить позже

Задача 4#97373

Докажите, что для любых единичных векторов на плоскости $v , 1$ $v ,...,v 2 n$ можно выбрать знаки в выражении $± v ±v ± ...± v 1 2 n$ так, что длина получившегося вектора будет не меньше чем $√ - n.$

Подсказки к задаче

Подсказка 1

Будем для удобства считать, что выбраны векторы u_i с учетом знака. Запишите квадрат суммы векторов. Что после этого нужно доказать?

Подсказка 2

Преобразованиями получите, что нужно взять векторы u_i так, чтобы сумма попарных скалярных произведений была неотрицательна. Как это можно сделать? Вообще у нас в условии n векторов, поэтому можно попробовать провернуть индукцию.

Подсказка 3

Докажите базу для двух векторов. Как реализовать переход? Выделите слагаемые, в которые входит новый вектор. Как бы сделать там сумму поменьше?

Показать доказательство

Пусть вектор $u1$ равен вектору $v1$ с выбранным перед ним знаком. Тогда результирующий вектор имеет вид $∑n i=1ui.$ Тогда достаточно показать, что знаки можно выбрать таким образом, что

( ) ∑n ∑n ∑ 2 ∑k k∑ n≤ i=1 ui,i=1ui = ui + 2i⁄=j(ui,uj)= n+2 i⁄=j(ui,uj)

то есть таким образом, что

∑k 0 ≤i⁄=j(ui,uj) (∗)

Докажем возможность такого выбора индукцией по $n.$ База для $n =2$ очевидна: скалярные произведения $(v1,v2)$ и $(v1,−v2)$ противоположны по знаку, а значит, хотя бы одно из них неотрицательно. Пусть для некоторого $k$ существует комбинация знаков при которой верно неравенство $(∗).$ Заметим, что

k+∑1 ( ∑k ) k∑ ( ∑k ) (ui,uj)= uk+1, ui + (ui,uj)≥(∗) uk+1, ui i⁄=j i=1 i⁄=j i=1

Сумма $∑k i=1ui$ фиксирована и не зависит от знака $uk+1,$ следовательно, достаточно положить такой знак $uk+1,$ что произведение $( ∑k ) uk+1, ui i=1$ неотрицательно.

Ошибка.
Попробуйте повторить позже

Задача 5#97374

Дан четырёхугольник $ABCD,$ в котором $AB = AD$ и $∠ABC = ∠ADC = 90∘.$ На сторонах $BC$ и $CD$ выбраны соответственно точки $F$ и $E$ так, что $DF ⊥ AE.$ Докажите, что $AF ⊥ BE.$

Подсказки к задаче

Подсказка

Самое сложно это грамотно ввести векторы. Как это сделать, чтобы их не было слишком много? Введите все векторы, которые чему-то перпендикулярны. Постарайтесь выразить через эти векторы условие и то, что требуется доказать.

Показать доказательство

Отрезки $AF$ и $DE$ перпендикулярны, следовательно, (здесь и далее в данной задаче, $XY ≡−X−Y→)$ получаем $(AE,DF )=0.$ Осталось заметить, что

(AE,DF )=(AE,DA + AF)= (AE,DA )+(AE,AF)=

2 2 = (AD + DE,DA )+(AE,AF )= −AD +(DE,DA )+(AE,AF )=− AB + (AE,AF)

= (AB +BF,BA )+(AE,AF )= (AF,BA )+(AE,AF )=(AF,BA +AE )= (AF,BE )

следовательно, отрезки $AF$ и $BE$ так же перпендикулярны.

$PIC$

Ошибка.
Попробуйте повторить позже

Задача 6#97377

Пусть $A A ...A 1 2 n$ — правильный $n$ -угольник, $X$ — произвольная точка. Рассмотрим проекции $X , 1$ $X ,...,X 2 n$ точки $X$ на прямые $A1A2,$ $A2A3,...,AnA1$ соответственно. Пусть $xi$ — длина отрезка $AiXi$ с учетом знака (знак плюс берётся в случае, когда лучи $AiXi$ и $AiAi+1$ сонаправлены). Докажите, что сумма $x1+ x2+...+xn$ равна половине периметра многоугольника $A1A2 ...An.$

Подсказки к задаче

Подсказка

Когда есть правильный многоугольник и вы хотите ввести векторы, очень полезно отметить его центр. Вам сразу легче становится выражать все векторы, а к тому же вы получаете прекрасное тождество - сумма векторов из O во все вершины равна 0. Сделайте это и в этой задаче, выразите все x_i через вектор OX, векторы выходящие из центра многоугольника и векторы сторон.

Показать доказательство

Достаточно рассмотреть случай, когда длины сторон многоугольника $A ...A 1 n$ равны $1.$ В этом случае $x = (A-X,−−A−−A−→) . i i i i+1$ Пусть $O$ — центр правильного многоугольника $A1...An.$ Тогда

∑n ∑n ( ) ( ∑n ) n∑ ( ) xi = −A−i→O,−−A−i−A−i+→1 + −−O→X, −−A−i−A−i+→1 = −A−i→O,−A−i−A−i−→+1 i=1 i=1 i=1 i=1

поскольку $∑n −−−−−→ −→ AiAi+1 = 0 i=1$ для любого многоугольника. Остаётся заметить, что

( −−→ −−−−−→ ) AiO,AiAi+1 = 1∕2

для всех $i.$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#97586

На плоскости нарисованы два квадрата $ABCD$ и $KLMN$ (их вершины перечислены против часовой стрелки). Докажите, что середины отрезков $AK$ , $BL$ , $CM$ и $DN$ являются вершинами квадрата.

Подсказки к задаче

Подсказка 1

Давайте подумаем, как можно доказать, что четырёхугольник является квадратом. Например, если доказать, что две соседние стороны равны и перпендикулярны, а потом сделать то же самое для других пар соседних сторон, то мы получим требуемое.

Подсказка 2

Реализовать задуманное можно через векторы. Если выразить векторы, соответствующие сторонам четырëхугольника, через векторы, про которые мы знаем побольше информации, а именно векторы сторон двух квадратов, то всё должно получиться.

Показать доказательство

Сформулируем и докажем следующюю лемму.

Лемма. Дан четырехугольник $ABCD$ , точки $M, N$ середины соотвественно сторон $AD$ и $BC$ , тогда

−→ −−→ −M−→N = AB-+-DC-. 2

Доказательство. Имеем

−−M→N = −−M→A + −A→B +−B−→N.

Аналогично

−M−N→ = −−M→D + −−D→C +−C−→N.

$PIC$

Поскольку $−M−A→ = −−M−→D$ и $−B−→N = −−C−→N$ , то, сложив полученные равенства и поделив на 2, получим требуемое.

_________________________________________________________________________________________________________________________________________________________________________________

Вернемся к доказательству исходной задачи. В силу леммы, имеем

−−→ −→ −−→ −→ −−→ −−→ PQ = AB-+-KL; QR = BC-+-LM- 2 2

Векторы $−→AB$ и $−K−→L$ получаются из векторов $−−B→C$ и $−L−M→$ поворотом на $90∘.$ Поэтому из приведенных выше равенств следует, что вектор $−Q→R$ получается из вектора $−−P→Q$ поворотом на $90∘,$ то есть отрезки $PQ$ и $QR$ равны и перпендикулярны. Аналогично, любые две стороны в четырехугольнике $P QRS$ равны и перпендикулярны.

$PIC$

Ошибка.
Попробуйте повторить позже

Задача 8#97590

Точка $K$ — середина стороны $AB$ квадрата $ABCD$ , а точка $M$ лежит на диагонали $AC$ , причём $AM :MC =3 :1.$ Докажите, что угол $KMD$ прямой.

Показать доказательство

Переведём задачу на язык векторов: $∠KMD$ прямой тогда и только тогда, когда скалярное произведение векторов $−M−K→$ и $−M−D→$ равно 0.

$PIC$

Выразим $−−→ MK$ через вектора $−→ AB$ и $−−→ AD$

−−→ −−→ −−→ 1−→ 3−→ 1−→ 3( −→ −−→ ) 1 −→ 3−−→ MK = AK − AM = 2AB − 4AC = 2AB − 4 AB+ BC = −4 AB − 4BC

Так как $ABCD$ — квадрат, то $−−→ −−→ AD = BC,$ тогда

−M−K→ = − 1−A→B − 3−B−→C =− 1−A→B − 3−A−→D 4 4 4 4

Выразим $−M−→D$ через вектора $−A→B$ и $−−A→D$

( ) −−M→D = −−A→D − −−A→M = −−A→D − 3 −A→C =−A−→D − 3 −A→B +−A−→D = 1 −−A→D − 3 −A→B 4 4 4 4

Теперь рассмотрим их скалярное произведение

−−→ −−→ ( 1−→ 3−−→ ) ( 1−−→ 3−→ ) -3−→ 2 3-−−→ 2 8-−→ −−→ MK ⋅MD = −4AB − 4AD ⋅ 4AD − 4AB = 16AB − 16AD + 16AB ⋅AD

Заметим, что раз $ABCD$ — квадрат, то $AB = AD$ и $∠BAD$ прямой, следовательно, $−→ 2 −−→2 AB = AD$ и $−→ −−→ AB ⋅AD = 0,$ тогда получаем

−−→ −−→ 3 3 MK ⋅MD = 16 − 16 = 0.

Значит, $∠KMD$ прямой.

Ошибка.
Попробуйте повторить позже

Задача 9#69116

В прямоугольнике $ABCD$ опущен перпендикуляр $BK$ на диагональ $AC.$ Точки $M$ и $N$ — середины отрезков $AK$ и $CD$ соответственно. Докажите, что угол $BMN$ прямой.

Подсказки к задаче

Подсказка 1

Давайте вспомним, как доказывать перпендикулярность, используя векторы? Конечно, мы должны доказать, что скалярное произведение MN и BM равно нулю. Для этого необходимо выразить эти векторы через попарно перпендикулярные: BC, BK, KC, AB

Подсказка 2

Так как скалярное произведение линейно по каждому аргументу, имеем, что MN * BM = 1/4 (BC * BK - KC * AB). Как используя перпендикулярность векторов (то есть BC * BA = KC * BK = 0) доказать, что BC * BK - KC * AB = 0?

Подсказка 3

Используйте, что BK = KC * ctg(α) и AB = BC * ctg(α), где ∠KBC = ∠BAC = α

Показать доказательство

$PIC$

Поскольку

( ) ( ) ( ) −M−N→ = 1 −A−→D + −−K→C = 1 −−B→C +−K−→C и −B−M→ = 1 −B→A + −−B→K 2 2 2

то

−−→ −−→ 1( −−→ −−→ ) (−→ −−→ ) 1 (−−→ −−→ −−→ −→ ) MN ⋅BM = 4 BC +KC ⋅ BA + BK = 4 BC ⋅BK +KC ⋅BA =

1( −−→ −−→ −−→ −→ ) = 4 BC ⋅BK −KC ⋅AB

Так как

−−→ −→ −−→ −−→ BC ⋅BA = KC ⋅BK = 0

Обозначим $∠BAC =∠KBC = α.$

Тогда

−−B→C ⋅−−B→K − −K−C→ ⋅−A→B = BC ⋅BK ⋅cosα − KC ⋅AB ⋅cosα =

= (BC⋅BK − KC ⋅AB)cosα= (BC⋅KC ctgα− KC ⋅BCctgα)cosα = 0.

Следовательно, $BM ⊥ MN.$

Ошибка.
Попробуйте повторить позже

Задача 10#69118

Пусть $O$ — центр окружности, описанной около равнобедренного треугольника $ABC$ $(AB =AC ),D$ — середина стороны $AB,$ а $E$ — точка пересечения медиан треугольника $ACD.$ Докажите, что $OE ⊥ CD.$

Подсказки к задаче

Подсказка 1

Нам нужно доказать, что какие-то две прямые перпендикулярны. Может, попробовать доказать, что направляющие векторы этих прямых перпендикулярны...

Подсказка 2

Два вектора перпендикулярны, когда их скалярное произведение равно 0. Может, как-то удобно выразить векторы EO и CD, чтобы посчитать их скалярное произведение...

Подсказка 3

Попробуйте выразить их через вектора OA, OC, OB. Например, вектор CD=1/2(CA+CB), где CA=CO+OA и CB=CO+OB.

Подсказка 4

Осталось выразить OE. Мы знаем, что OE=OA+AE, а AE=1/3(AD+AC). Как же тогда выражается OE через OA, OC, OB?

Подсказка 5

OE=1/6(3OA+2OC+OB). Проверьте, что скалярное произведение действительно равно нулю, и радуйтесь!

Показать доказательство

$PIC$

( ) −−O→D = 1 −O→A + −−O→B 2

Поэтому

−−→ 1 (−→ −−→ −−→ ) 1( −→ −−→ 1(−→ −−→) ) OE = 3 OA +OC + OD = 3 OA+ OC + 2 OA + OB = = 1(3−O→A + 2−−O→C+ −O−→B ) 6

Кроме того,

−−→ 1 (−→ −−→ ) 1 ((−−→ −→ ) (−−→ −−→ )) CD = 2 CA +CB = 2 CO + OA + CO + OB = 1 (−→ −−→ −−→) = 2 OA +OB − 2OC

Значит,

( ) ( ) 12−O−→E ⋅−C−→D = 3−O→A +2−O−→C + −−O→B ⋅ −O→A +−O−→B − 2−−O→C =

= 3−O→A2 + 3−O→A ⋅−O−→B − 6−O→A ⋅−O−→C + 2−O−→C ⋅−O→A + 2−O−→C ⋅−O−→B − 4−O−→C2+

+−O→A ⋅−−O→B +−O−→B2 − 2−O−→B ⋅−−O→C =

−→ −−→ −→ −−→ = 3R2 − 4R2 +R2 +4OA ⋅OB − 4OA ⋅OC =

−→ (−−→ −−→ ) −→ −−→ = 4OA OB − OC = 4OA ⋅CB = 0

Так как $OA ⊥ BC$ ( $R$ — радиус окружности). Следовательно, $OE ⊥CD.$

Ошибка.
Попробуйте повторить позже

Задача 11#34678

Точка $O$ является центром окружности, описанной около треугольника $ABC$ со сторонами $BC = 8$ и $AC = 4$ . Найдите длину стороны $AB$ , если длина вектора $−→ −−→ −−→ 4OA −OB − 3OC$ равна $10$ .

Источники: ОММО-2022, номер 4, (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

В таких задачах на счет нужно очень четко понять, какие переменные мы вводим и зачем это делать. Какие переменные у нас уже известны? Две стороны треугольника. Значит, если попробовать выразить наше выражение векторное, через часть из известных переменных и того, что нам нужно найти, то может что-то получится.

Подсказка 2

Давайте выразим каждый из векторов в выражении через векторы CA и AB, тогда выходит, что |3AC + AB| = 10 (здесь написаны векторы). Далее, нам ничего не остается как возводить в квадрат, но там вылезет косинус из произведения векторов. Как побороть эту проблему, если у нас в виде переменных остаются AB и cos(BAC).

Подсказка 3

Конечно, у нас есть cos(BAC) и AB, значит все намекает на теорему косинусов для треугольника ABC и стороны BC. Вычтя из нашего равенства, которое получилось возведением в квадрат модуля, равенство из теоремы косинусов, получим уравнение, в котором есть AB*cos(BAC), приравненное к константе. Что тогда можно сделать, чтобы найти AB?

Подсказка 4

Само собой, остается подставить это в уравнение, полученное из модуля, так как после подстановки, там останется одна неизвестная - AB, а значит, задача решена!

Показать ответ и решение

$PIC$

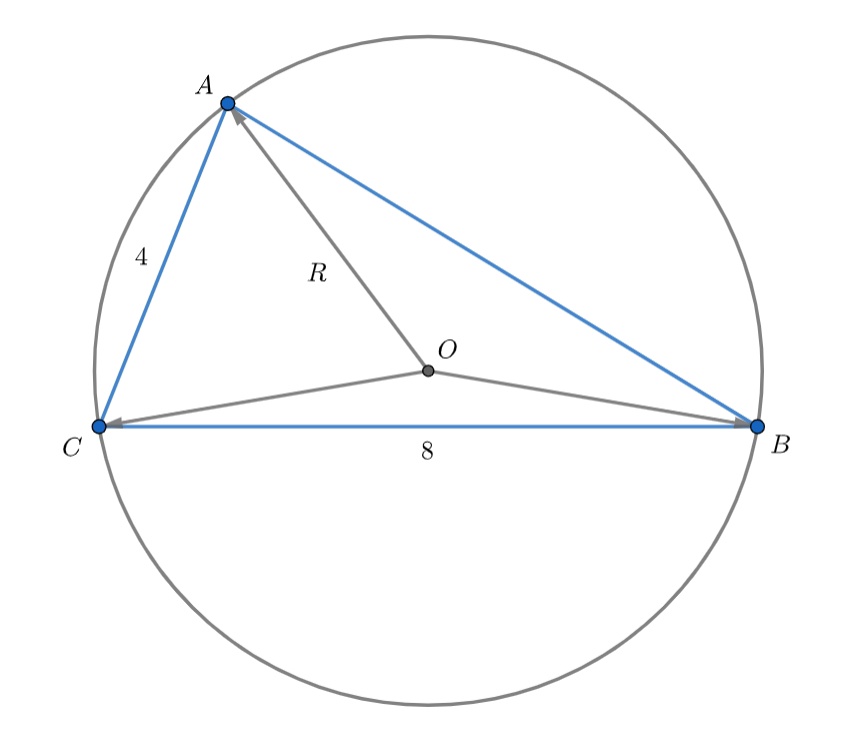
Будем пользоваться тем, что скалярный квадрат вектора равен квадрату длины вектора.

Из условия получаем, что

|3−−→CO+ 3−O→A +−B−→O + −O→A|= 10

то есть

−→ −→ |3CA+ BA|= 10

то есть

−→ −→ |3AC + AB|= 10.

А теперь возведём обе части в квадрат:

9AC2 + AB2+ 6AC ⋅AB ⋅cos∠BAC = 100.

По теореме косинусов из треугольника $ABC$ имеем

2 2 2 AC + AB − 2AC ⋅AB ⋅cos∠BAC = BC .

Вычитая это равенства из полученного выше, получаем:

8AC2+ 4AB ⋅AC ⋅cos∠BAC =100− BC2

С учётом $AC = 4,BC = 8$ имеем:

8⋅16 +8⋅4⋅AB ⋅cos∠BAC =36 ⇐⇒ 8AB ⋅cos∠BAC = 9− 32

Итак, $16+ AB2 +23= 64 ⇐⇒ AB =5$

Ответ:

$5$

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#72245

В треугольнике $ABC$ синус угла $A$ равен $3∕5.$ На стороне $AC$ взяли точку $M$ так, что $CM =15,$ на стороне $AB$ взяли точку $N$ так, что $BN = 7,AN = AM,$ $T$ — середина $NC,$ $P$ — середина $BM.$ Найдите длину отрезка $PT.$ Если возможных ответов несколько, введите их сумму. Ответ округлите до десятых.

Источники: Муницип - 2022, Республика Башкортостан, 10.4

Подсказки к задаче

Подсказка 1

У нас отмечены две середины, может, стоит поискать средние линии? Попробуйте придумать какую-нибудь среднюю линию с точкой T...

Подсказка 2

Можно взять точку L- середину BC. Тогда TL- средняя линия треугольника △NCB ⇒ TL=7/2 и TL // AB. А что мы можем сказать про PL?

Подсказка 3

Это тоже средняя линия, только для треугольника △MBC ⇒PL=15/2 и PL // AC. Из параллельности следует, что уголок ∠PLT равен ∠BAC. Можем ли мы уже найти PT?

Подсказка 4

Конечно можем, ведь у нас есть теорема косинусов! Доведите решение до конца и не забудьте, что cos(∠BAC) может принимать два значения...

Показать ответ и решение

$PIC$

Обозначим длины $AN$ и $AM$ за $x.$ Введём систему из двух единичных векторов: пусть вектор $−→ b$ коллинеарен вектору $−→ AB,$ а вектор $−→c$ коллинеарен вектору $−A→C.$ Тогда верны векторные соотношения:

−→PT =−A→T − −→AP,−A→P = 1(−A→B + −−A→M ),−A→T = 1(−→AC+ −−A→N ) 2 2 −→AB = (x+ 7)⃗b,−→AC = (x+ 15)⃗c, −A−→M = x⃗c, −A−→N = x⃗b −→ 1 −→ −−→ −→ −−→ 1 ⃗ P T = 2(AC +AN − AB −AM )= 2(15⃗c− 7b)

Вычисляя скалярный квадрат вектора $−→ PT,$ и учитывая, что косинус угла $\text{[math]}$ может быть равен равен $4∕5$ для острого угла и $− 4∕5$ для тупого, получим

−→ −→ 1 PT ⋅PT = 4(49⃗b⋅⃗b+225⃗c⋅⃗c− 210⃗b⋅⃗c)= 26,5 −→ −→ 1 ⃗⃗ ⃗ PT ⋅PT = 4(49b⋅b+225⃗c⋅⃗c− 210b⋅⃗c)= 110,5

Ответ: 15.7

Ошибка.
Попробуйте повторить позже

Задача 13#34679

В треугольнике $ABC$ длины сторон равны $4$ , $5$ и $√17-$ . Найдите площадь фигуры, состоящей из тех и только тех точек $X$ внутри треугольника $ABC$ , для которых выполняется условие $2 2 2 XA +XB + XC ≤21$

Источники: ОММО - 2021, номер 4 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Расстояния между точками удобно считать, когда есть система координат. Как было бы удобно расположить наш треугольник в декартовой системе координат?

Подсказка 2

Заметим, что высота, проведенная к стороне длины 4, равна целочисленному числу, поэтому удобно ввести систему координат так, чтобы Оу было вдоль этой высоты, а Ох — вдоль упомянутой стороны треугольника. Тогда координаты вершин треугольника принимают целочисленные значения.

Подсказка 3

Пусть (x; y) — координаты X. Тогда выражение XA² + XB² + XC² можно представить как сумму двух квадратов с некоторыми коэффициентами, что очень напоминает уравнение окружности с центром в (x; y). А так как нам дано неравенство, то наша фигура в X — это круг! Останется лишь показать, что все его точки лежат внутри △ABC.

Показать ответ и решение

Первое решение. Обозначим $BC = a,AC = b,AB = c,ρ2 =21$ .

Докажем утверждение, известное как теорема Лейбница в геометрии. Пусть $G$ - точка пересечения медиан треугольника $ABC$ . Представим

−−→ −→ −−→ −−→ −−→ −−→ −−→ −−→ −−→ XA =GA − GX,XB = GB − GX,XC = GC −GX,

тогда

2 2 2 2 2 2 −−→ −→ −−→ −−→ 2 XA + XB +XC = GA + GB +GC − 2⋅GX ⋅(GA + GB +GC )+3⋅GX

Поскольку $G−$ центр тяжести треугольника $ABC$ , то

−G→A +−G−→B + −−G→C = 0,

GA2+ GB2 +GC2 = 4(m2a +m2b + m2c)= 1(a2+ b2+ c2) 9 3

С учётом доказанной выше теоремы задача эквивалентна

1(a2+ b2 +c2)+3 ⋅GX2 ≤ ρ2, 3

то есть неравенство сводится к

GX2 ≤ 1⋅(3ρ2− a2− b2 − c2). 9

Итак, геометрическим местом точек $X$ , удовлетворяющих поставленному условию, является круг радиуса $1∘3ρ2−-a2−-b2−-c2 3$ с центром в точке пересечения медиан треугольника $ABC$ .

Этот круг принадлежит треугольнику, если его радиус не больше, чем одна треть наименьшей из высот $△ABC$ :

1∘--2--2---2--2- -2S△ABC--- 3 3ρ − a − b − c ≤ 3max{a,b,c}.

Значит, при выполнении условия

2 2 2 2 2 2 ( )2 a-+b-+-c-< ρ2 ≤ a-+-b-+-c + 4 ⋅-S△ABC-- 3 3 3 max{a,b,c}

искомая площадь равна $S = π ⋅(3ρ2− a2− b2− c2) 9$ . По формуле Герона найдем площадь треугольника:

1∘----√------√---√------√------ S△ABC = 4 (9+ 17)(9− 17)( 17+ 1)( 17− 1)=8

Вычислим

a2 +b2+ c2 58 S△ABC 8 ---3-----= 3-,max{a,b,c}-= 5

Поскольку $ρ2 = 21$ , условие $(∗)$ выполняется:

58 <21≤ 58+ 256= 1706 3 3 75 75

Значит, ответ: $S = π9 ⋅(63− 58)= 5π9$ .

Второе решение. Высота треугольника, проведенная к стороне длины $4$ , равна $4$ . Основание высоты делит эту сторону на отрезки, равные $1$ и $3$ . Введем систему координат так, как показано на рисунке. Тогда $A(−1;0),B(0;4),C(3;0)$ .

$PIC$

$2 2 2 2 2 2 2 2 2 2 2 XA + XB +XC = (x+ 1) + y + x +(y− 4) + (x− 3) + y =3x + 3y − 4x− 8y+ 26 ≤21.$ Перепишем неравенство так:

( )2 ( )2 x − 2 + y− 4 ≤ 5. 3 3 9

Оно определяет круг радиуса $R = √35$ с центром в точке $K (2∕3;4∕3)$ . Покажем, что все точки этого круга принадлежат треугольнику $ABC$ . Для этого найдем расстояния от точки $K$ до сторон треугольника. Уравнение стороны $AB :4x− y+ 4= 0$ , расстояние до неё равно $|4⋅√(2∕3)−4∕3+4| d1 = 42+(−1)2 =$ $-1√6- = 3 17$ . Уравнение стороны $BC :4x+3y− 12= 0$ , расстояние $|4⋅(2∕3√)+3⋅(4∕3)−12| 16 d2 = 42+32 = 15$ . И расстояние от точки $K$ до стороны $AC$ равно, очевидно, $d3 = 43$ . Наименышее из расстояний $d2$ , тем не менее, больше, чем радиус круга $√- R : 1615-> 35$ . Поэтому весь круг и является той фигурой, площадь которой требуется найти, откуда $S =πR2 = 59π$ .

Ответ:

$5π 9$

Ошибка.
Попробуйте повторить позже

Задача 14#92430

В первой четверти координатной плоскости отметили две точки $A$ и $B$ с целочисленными координатами. Оказалось, что $∘ ∠AOB =45$ , где $O$ — начало координат. Докажите, что хотя бы одна из четырёх координат точек $A$ и $B$ — чётное число.

Источники: Курчатов - 2021, 11.3 (см. olimpiadakurchatov.ru)

Подсказки к задаче

Подсказка 1

Как мы можем связать угол и координаты этих точек? Через скалярное произведение. Запишите его и подумайте над тем, что с ним можно сделать, если знать, что все координаты - целые числа.

Подсказка 2

Мы можем возвести в квадрат, чтобы избавиться от иррациональности. Теперь положим, что все числа нечётные. Что нам это даёт? Какой остаток по модулю 4 дает любой нечётный квадрат? А что тогда можно сказать про степень вхождения двойки в левую и правую части?

Показать доказательство

Пусть точка $A$ имеет целочисленные координаты $(a;b)$ , а точка $B$ — $(c;d)$ . Запишем скалярное произведение векторов $−O→A (a;b)$ и $−−→ OB (c;d)$ двумя способами: через координаты и через угол между ними.

−→ −−→ −→ −−→ ∘ ------∘ ------ 1 ac+ bd= OA⋅OB = |OA |⋅|OB |cos45∘ = a2+ b2⋅ c2+d2⋅√2-, откуда 2 ( 2 2)( 2 2) 2(ac+bd) = a + b c + d .

Предположим, все числа $a,b,c,d$ нечётны, тогда все выражения в скобках являются чётными числами. Квадрат любого нечётного числа даёт остаток 1 при делении на 4 (поскольку $(2k+ 1)2 = 4(k2+ k) +1$ ), поэтому каждая из скобок в правой части является чётным числом, не делящимся на 4 . Получаем противоречие с тем, что левая часть равенства делится на $2⋅22 =8$ , а правая на 8 не делится.

Ошибка.
Попробуйте повторить позже

Задача 15#47137

Пусть $L$ — точка пересечения диагоналей $CE$ и $DF$ правильного шестиугольника $ABCDEF$ со стороной $3.$ Точка $K$ такова, что $−−→ −→ −→ LK = 3AB −AC.$ Определите, лежит ли точка $K$ внутри, на границе или вне $ABCDEF,$ а также найдите длину отрезка $KC.$

Источники: ОММО-2017, номер 4, (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Заметим несколько фактов: в правильном шестиугольнике CE перпендикулярно FE и AB при проекции на EF или CB равняется EF/2. Попробуйте использовать эти два факта!

Подсказка 2

Пусть К' - точка пересечения AB и CE. Теперь мы можем использовать вектор CK' для выражения, попробуем найти равный ему вектор!

Подсказка 3!

Верно, это LK! Осталось правильно применить все полученные на рисунке векторы!

Показать ответ и решение

$PIC$

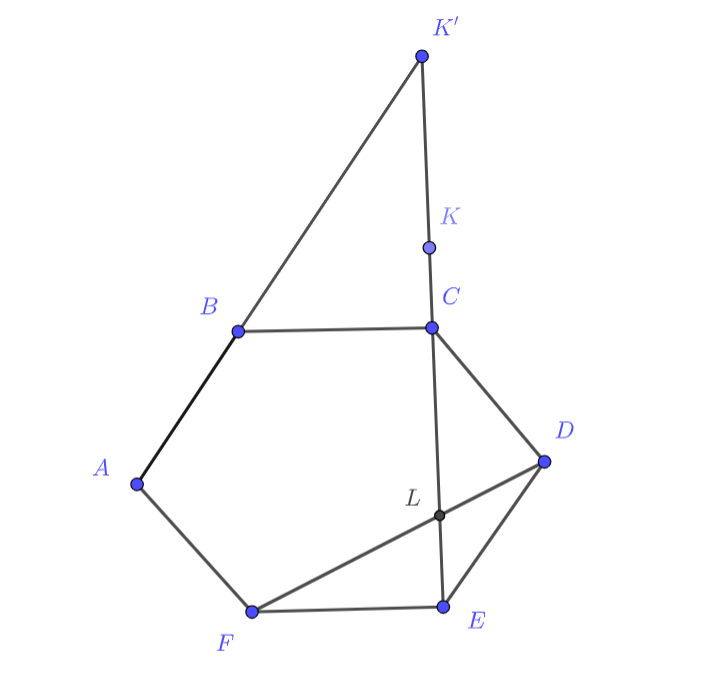
Как известно, $CE ⊥ FE,$ а также проекция $AB$ на прямую $FE$ равна $FE2 .$ Поэтому если продлить $AB$ в три раза до точки $K′,$ то $K ′ ∈CE$ (удвоенная проекция $AB$ равна $F E$ ). Отсюда легко видеть, что $−A→C + −C−K→′ =3−A→B,$ то есть $−C−K→′ = −−L→K.$ По свойствам правильного шестиугольника

CE = √3AB = AB tg60∘ = BC tg ∠K′BC =CK ′

В итоге $CE =LK = CK ′ =⇒ LE = CK = FE⋅tg∠DF E = √3.$

Ответ:

Вне, $√3$

Ошибка.
Попробуйте повторить позже

Задача 16#47911

В треугольнике $ABC$ с отношением сторон $AB :AC =5 :4$ биссектриса угла $BAC$ пересекает сторону $BC$ в точке $L.$ Найдите длину отрезка $AL,$ если длина вектора $−→ −→ 4⋅AB +5⋅AC$ равна $2016.$

Источники: ОММО-2016, номер 4, (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Давайте пробовать постепенно раскручивать задачу, пользуясь всеми условиями. Нам дана биссектриса треугольника. Какие тогда соотношения можно записать?

Подсказка 2

Верно, можно записать равенство отношений отрезков и сторон, тем более одно из них нам дано. Так же нам дали какую-то странную сумму векторов... Давайте тогда попробуем выразить AL через вектора, может эта сумма там и появится. Как это можно сделать?

Подсказка 3

Ага, можно для начала выразить AL через сумму двух векторов по правилу треугольника. Видим, что фигурируют неизвестные нам вектора, и в данной по условию сумме они не участвуют. Тогда попробуем заменить один из векторов по полученному равенству в 1 подсказке, а далее ещё раз воспользоваться правилом треугольника.

Показать ответ и решение

$PIC$

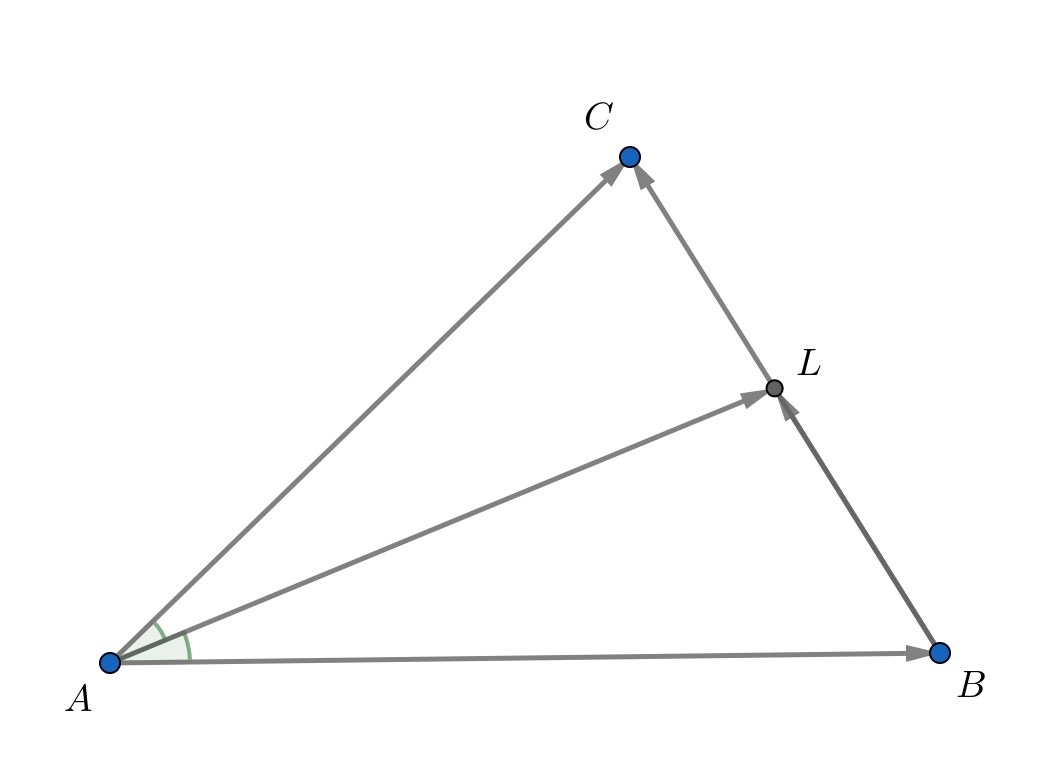
Поскольку по свойству биссектрисы $BLLC-= AABC-= 54,$ то $−→ −−→ BL= 59BC,$ тогда

( ) −A→L = −A→B +−B→L = −A→B + 5⋅−−B→C = −→AB+ 5 −A→C − −A→B = 9 9

= 4 ⋅−A→B + 5 ⋅−A→C = 1 (4−→AB+ 5−−B→C) 9 9 9

Отсюда $−→ 1 |AL |= 9 ⋅2016= 224.$

Ответ:

$224$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 17#76408

В треугольнике $ABC$ точки $A ,B ,C − 1 1 1$ середины сторон $BC,AC$ и $AB$ соответственно. Найдите длину стороны $AC$ , если известно, что сумма векторов

−−→ −−→ −−→ 3⋅AA1+ 4⋅BB1+ 5⋅CC1

равна вектору с координатами $(2,1).$

Подсказки к задаче

Подсказка 1

Самое главное в этой задаче — это удобно ввести обозначения. Пусть середина каждого из отрезков равна a, b, c. Но надо правильно выбрать направления. Почему треугольник в данном случае очень полезен?

Подсказка 2

Верно, если задать все направления по часовой стрелке, то просто сумма 2a+2b+2c=0, так как мы вернулись в начальную точку треугольника. А теперь нужно подставить в формулу из условия выражения через наши векторы. Попробуйте это сделать. Хорошо бы было получить в итоге просто один вектор, так как теперь нам будут известны его координаты. Но через какой удобнее всего будет выразить?

Подсказка 3

Да, вспомним в принципе условие задачи. Нам нужно найти длину стороны, а значит, через этот вектор и будет удобно выразить всю сумму(например, если AC = |2b|, то через b). Осталось только вспомнить, что через координаты вектора можно найти его длину, и победа!

Показать ответ и решение

Обозначив

−−→ ⃗ −→ −→ 2⃗a= BC, 2b= CA и 2⃗c= AB,

$PIC$

получаем

−→ 2⃗a+ 2⃗b+2⃗c= 0

−→ −−→ −−→ (2,1)= 3⋅AA1+ 4⋅BB1 +5 ⋅CC1 = 3(2⃗c+ ⃗a)+4(2⃗a +⃗b)+ 5(2⃗b+⃗c)=

⃗ ⃗ ⃗ =4(2⃗a+ 2b+ 2⃗c)+4(⃗a+b +⃗c)− (2⃗c+⃗a)+ (2b +⃗c)=

=−→0 + −→0 − (⃗a+ ⃗b+ ⃗c)+ 3⃗b= 3⃗b⇒

| | | | √-2--2- √- ⇒ AC = |2⃗b|= |||2⋅3⃗b|||=|||2 ⋅(2;1)|||= 2-2-+-1-= 2-5 3 3 3 3

Ответ:

$2√5 3$

Ошибка.
Попробуйте повторить позже

Задача 18#76409

Основания $AB$ и $CD$ трапеции $ABCD$ равны 65 и 31 соответственно, а её диагонали взаимно перпендикулярны. Найдите скалярное произведение векторов $−−→ AD$ и $−−→ BC.$

Источники: ОММО - 2015, задача 4, и Газпром - 2022, задача 3 (9-11 классы)

Подсказки к задаче

Подсказка 1

Перед нами трапеция, у которой мы знаем соотношение оснований, а посчитать нам хочется модули векторов- значит, попробуем посчитать всевозможные отрезки на чертеже!

Подсказка 2

Нам известно, как выглядит скалярное произведение векторов, которые мы можем выразить как сумму векторов, выраженных через друг друга. Теперь нужно его записать и использовать угол!

Подсказка 3

Нужное скалярное произведение есть 31/65 от суммы квадратов длин векторов AO и BO. А как учесть угол?)

Показать ответ и решение

Пусть $O$ - точка пересечения диагоналей $AC$ и $BD$ . Из подобия треугольников $AOB$ и $COD$ следует, что $−O−→C = 31−→AO 65$ , а $−−→ 31−−→ OD = 65BO$ . Обозначим вектор $−→ AO$ через $⃗a$ , а вектор $−−→ BO$ через $⃗b$ . Тогда, из условия следует, что $(⃗a,⃗b)= 0$ и

−−→ −→ −−→ 31 −−→ −−→ −−→ 31 AD =AO + OD = ⃗a+ 65⃗b, BC =BO + OC =⃗b+ 65⃗a

$PIC$

Откуда

−−→ −−→ ( 31⃗ ⃗ 31-) 31( 2 ⃗2) ⃗ 31 2 (AD,BC) = ⃗a +65b,b+ 65⃗a = 65 |⃗a| + |b| + (...)⋅(⃗a,b)= 65|AB | =2015,

где предпоследнее равенство следует из того, что треугольник $AOB$ - прямоугольный.

Ответ: 2015

Ошибка.
Попробуйте повторить позже

Задача 19#97375

Будем называть четырехугольник равнодиагональным, если у него равны диагонали. Отрезок, соединяющий середины двух противоположных сторон выпуклого четырехугольника $ABCD,$ делит его на два равнодиагональных четырехугольника. Докажите, что четырехугольник $ABCD$ сам равнодиагональный.

Источники: СПБГОР - 2013, 10.2(см. www.pdmi.ras.ru)

Подсказки к задаче

Подсказка

Как переписать условие задачи на язык векторов? Введите векторы сторон, из них легко выразить условие задачи. Как из двух условий получить утверждение задачи?

Показать доказательство

Первое решение

Без ограничений общности будем считать, что указанный отрезок соединяет середины сторон $AB$ и $CD.$ Введем вектора $a,b,c,d$ таким образом, что

−→ −−→ −−→ −−→ AB =2a,BC = 2c,CD = 2b,DA = 2d

$PIC$

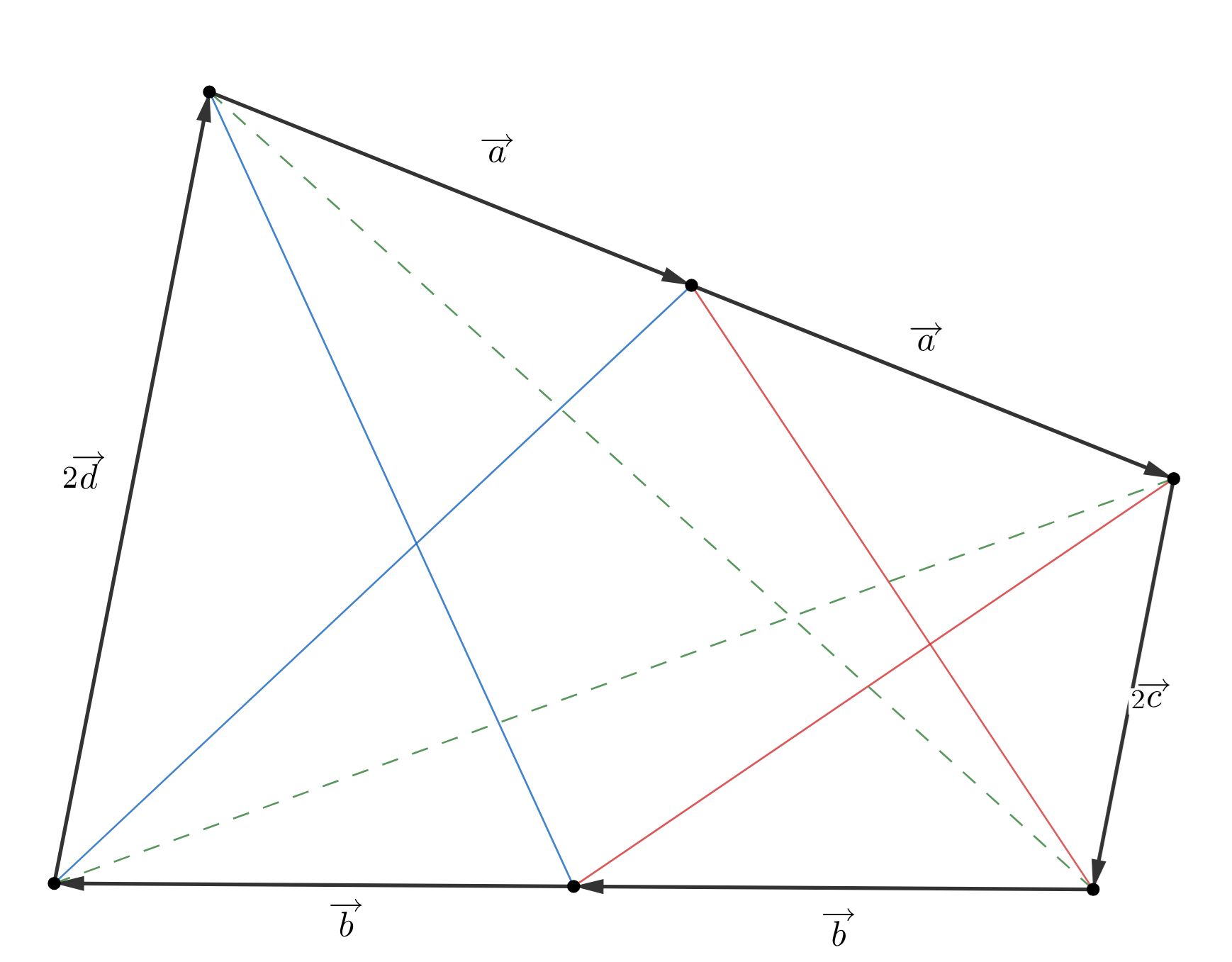
Поскольку диагонали образованных четырехугольников равны имеют место равенства

(2c+a)2 = (b+ 2c)2;(a +2d)2 =(2d+ b)2

Здесь и далее, для любых двух векторов $u,v :u⋅v = (u,v).$ Таким образом, вычитая второе равенство из первого, получим

2(a− b)(a +b+ c)=2(a− b)(a+ b+d)

(a− b)(c− d)= 0

Поскольку $a+ b+ c+d =0,$ имеем

(a− b)(a+ b+2c)= 0

(a+c)2 = (b+ c)2

следовательно, диагонали исходного четырехугольника так же равны.

_________________________________________________________________________________________________________________________________________________________________________________

Второе решение

Пусть $K$ и $M$ — середины сторон соответственно $AB$ и $CD$ четырёхугольника $ABCD.$ Из признака равенства треугольников по двум сторонам и медиане, проведённой к третьей следует равенство треугольников $CKD$ и $BMA,$ поэтому $CD = AB,$ а значит, $CM = BK.$ Треугольники $KBC$ и $MCB$ равны по трём сторонам, поэтому $∠BKC =∠BMC.$ Тогда

∠AKC = 180∘− ∠BKC =180∘− ∠BMC = ∠BMD

Тогда треугольники $AKC$ и $DMB$ равны по двум сторонам и углу между ними, следовательно, $AC = BD.$

Ошибка.
Попробуйте повторить позже

Задача 20#97372

В треугольнике $ABC$ точка $O$ — центр описанной окружности, $M$ — середина стороны $AB,$ $E$ — точка пересечения медиан треугольника $ACM.$ Известно, что отрезки $OE$ и $CM$ перпендикулярны. Докажите, что треугольник $ABC$ равнобедренный.

Подсказки к задаче

Подсказка 1

Для начала стоит ответить на 2 вопроса. Какие стороны в треугольники должны быть равны? Какие векторы можно ввести?

Подсказка 2

Порисовав картинки можно понять, что хочется доказывать, что AB = AC. В условии спрашивается что-то про равенство отрезков, поэтому удобно ввести векторы a=OA, b=OB, c=OC. Они все равны по длине, а еще через них выражаются все условия. Сделайте это. Как теперь доказывать, что какие-то 2 стороны равны?

Подсказка 3

Аккуратно напишите через векторы OA, OB и OC перпендикулярность из условия, поймите из нее, что (a,b) = (a,c). Почему это равносильно тому, что AB = AC? Вспомните про косинус и докажите это.

Показать доказательство

Введем векторы $a= OA,b= OB,c= OC.$ Без ограничений общности будем, считать, что описанная окружность имеет единичный радиус, в частности, $|a|= |b|=|c|= 1.$ Тогда