Длины векторов и скалярное произведение
Ошибка.
Попробуйте повторить позже
Выпуклый шестиугольник описан около окружности
с центром в
Оказалось, что
и описанная окружность
треугольника
концентричны. Обозначим через
основание перепндикуляра из
на
Прямая, перпендикулярная
проходящая через
пересекает прямую
в точке
Пусть
— основание перпендикуляра из
на
Докажите, что
Источники:
Подсказка 1
Для начала хочется заметить любые факты на картинке. Что можно искать? Что можно отметить? Для начала можно отметить все касания окружности со сторонами. Постарайтесь найти какие-нибудь перпендикулярные прямые и пересекающиеся в одной точке 3 прямые. Что делать дальше?
Подсказка 2
Найдите прямые перпендикулярные BO, а так же пару прямых, пересекающуюся на DF, полезно вспомнить про полюс и поляру. Как теперь можно ввести векторы?
Подсказка 3
Введите векторы OY, для всех точек Y, которые участвуют в какой-нибудь перпендикулярности. Через эти векторы перепишите все условия и вопрос задачи, если сделать все правильно, то у вас обязательно решится задача.
Обозначим точки касания и
с
через
и
соответственно. Заметим, что
Симметрия относительно отображает
в
следовательно,
в
и, следовательно, также
в
Таким образом, обе
прямые
и
перпендикулярны
следовательно, они параллельны. С другой стороны, прямые
и
не
параллельны, так как в противном случае шестиугольник
симметричен относительно прямой
и прямой,
определяющие точку
совпадают, что противоречит условию. Поэтому мы можем рассмотреть точку
пересечения
и
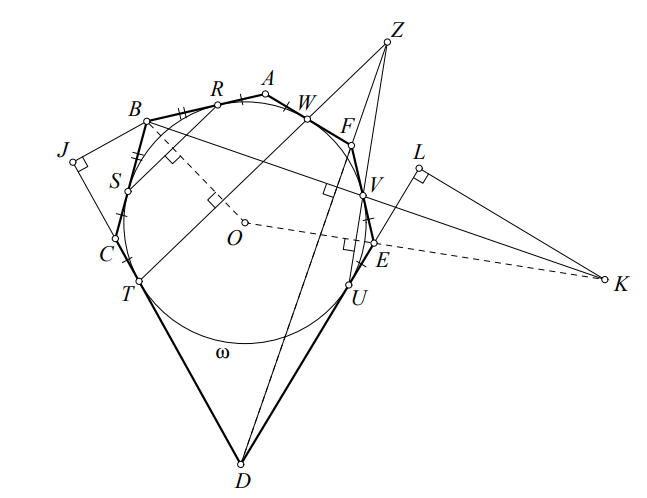
Далее напомним известный факт, что точки лежат на одной прямой. Действительно,
— это полюс прямой
— полюс
поэтому все эти точки принадлежат поляре точки пересечения
и
Рассмотрим систему координат, в которой является началом координат и отождествим каждую точку (скажем,
с вектором
Далее, мы полагаем, что для любых двух точек
и
Поскольку и
имеем
Далее, условие
можно записать как
Сложив эти два равенства, получим
Из симметрии имеем Вычитая из предыдущего уравнения, получим
Переписывая его в векторной форме, получим
Наконец, проецируя векторы и
на прямые
и
соответственно, мы можем переписать это равенство в терминах длин
отрезков как
следовательно,
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




