Тетраэдр в параллелепипеде
Ошибка.
Попробуйте повторить позже
В тетраэдре скрещивающиеся рёбра попарно равны. Через середину отрезка
, где
- точка пересечения высот грани
, провели прямую
перпендикулярно плоскости
. Аналогичным образом определили точки
,
и построили
прямые
соответственно для трёх других граней тетраэдра. Докажите, что прямые
пересекаются в одной
точке.
Источники:
Подсказка 1.
Самый простой способ доказать, что несколько прямых пересекаются в одной точке - определить эту точку, а затем доказать, что все прямые через неё проходят. Попробуйте доказать, что данные прямые проходят через центр описанной сферы тетраэдра(точку O).
Подсказка 2.
Просто так работать с этим объектом не получается. Попробуем воспользоваться равенством скрещивающихся рёбер ABCD. Проведём через каждые пары скрещивающихся рёбер параллельные плоскости. Тогда какую фигуру мы получаем в качестве пересечения этих плоскостей?
Подсказка 3.
Да, верно! Это же прямоугольный параллелепипед! Тогда точка O является его центром(пусть A',B',C',D' - точки, симметричные A,B,C,D относительно O). Отметим точку пересечения медиан треугольника BCD (точка M). Попробуйте разложить векторы AM и AA' через векторы A'B,A'C,A'D.
Подсказка 4.
Мы получаем, что точка M лежит на AA' и A'M/AM = 1/2, то есть AO/OM = 3/1. Отлично! Теперь осталось доказать, что перпендикуляр, опущенный из O на BCD, проходит через середину AH(где H - ортоцентр треугольника BCD). Для этого рассмотрим проекцию на BCD(пусть A" - проекция A, O1 - проекция O). Мы знаем, что проекция прямой AM проходит через точку пересечения медиан и центр описанной окружности. Что же это тогда за прямая?
Подсказка 5.
Да это же прямая Эйлера! А значит, она проходит и через ортоцентр треугольника BCD. Теперь, используя, что MH = 2MO1, попробуйте получить отношение отрезков A"O1 и O1H.
Подсказка 6.
Отлично! Мы знаем, что A"O1 = O1H. Тогда что можно сказать про отношение отрезков, на которые разбивается AH прямой OO1?
Проведём через пару скрещивающихся рёбер тетраэдра две параллельные плоскости. Так же поступим для двух других пар
скрещивающихся рёбер и получим параллелепипед. Диагонали его граней равны между собой, поэтому все грани — прямоугольники, и
параллелепипед прямоугольный. Пусть
— его центр, являющийся также центром описанной сферы тетраэдра
Пусть также
— точки, симметричные
соответственно относительно точки
Докажем, что все построенные прямые проходят
через точку
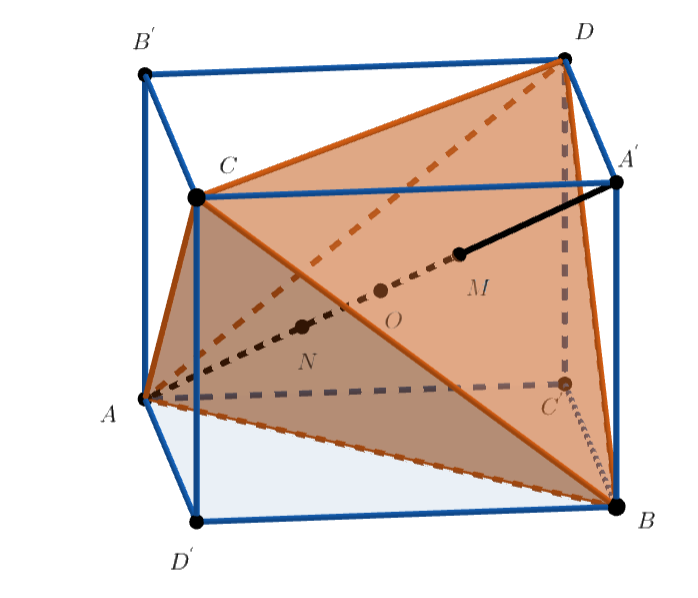
Пусть — центр масс треугольника
. Тогда
То есть точка лежит на диагонали
и делит её в отношении
, считая от вершины
Аналогично центр масс
треугольника
лежит на этой диагонали и делит её в отношении
, считая от вершины
Точка
— середина отрезка
поэтому
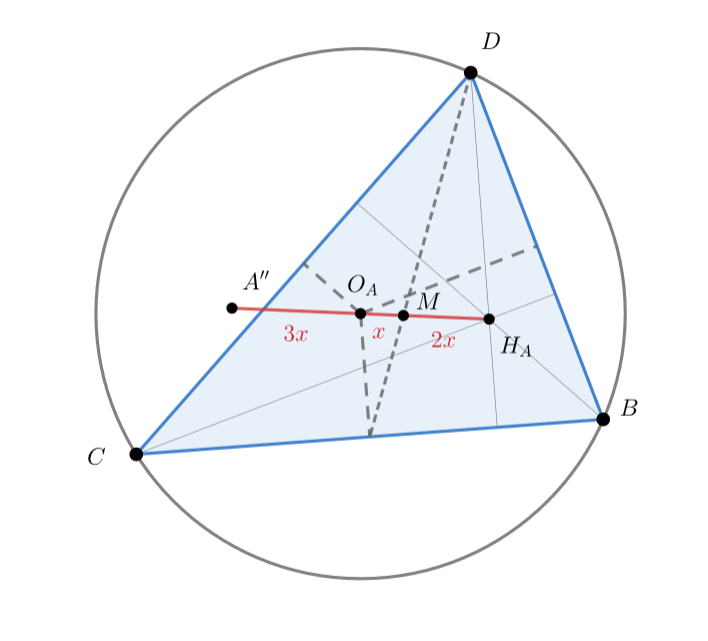
Рассмотрим проекцию на плоскость
— проекция точки
,
— проекция центра
Точка
совпадает с центром
описанной сферы тетраэдра
поэтому
— центр описанной окружности треугольника
Тогда прямая проецируется в прямую Эйлера
треугольника
Пусть
Тогда
(
делит
отрезок
в отношении
, это отношение сохраняется при проецировании). Кроме того,
лежат на одной прямой и
(прямая Эйлера), отсюда
Следовательно,
, а прямая
, перпендикулярная
плоскости
, делит отрезок
пополам, а значит, совпадает с прямой
. Итак, все построенные прямые проходят через точку
.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




