Тетраэдр в параллелепипеде
Ошибка.
Попробуйте повторить позже
В тетраэдре скрещивающиеся рёбра попарно равны. Через середину отрезка
, где
- точка пересечения высот грани
, провели прямую
перпендикулярно плоскости
. Аналогичным образом определили точки
,
и построили
прямые
соответственно для трёх других граней тетраэдра. Докажите, что прямые
пересекаются в одной
точке.
Источники:
Подсказка 1.
Самый простой способ доказать, что несколько прямых пересекаются в одной точке - определить эту точку, а затем доказать, что все прямые через неё проходят. Попробуйте доказать, что данные прямые проходят через центр описанной сферы тетраэдра(точку O).
Подсказка 2.
Просто так работать с этим объектом не получается. Попробуем воспользоваться равенством скрещивающихся рёбер ABCD. Проведём через каждые пары скрещивающихся рёбер параллельные плоскости. Тогда какую фигуру мы получаем в качестве пересечения этих плоскостей?
Подсказка 3.
Да, верно! Это же прямоугольный параллелепипед! Тогда точка O является его центром(пусть A',B',C',D' - точки, симметричные A,B,C,D относительно O). Отметим точку пересечения медиан треугольника BCD (точка M). Попробуйте разложить векторы AM и AA' через векторы A'B,A'C,A'D.
Подсказка 4.
Мы получаем, что точка M лежит на AA' и A'M/AM = 1/2, то есть AO/OM = 3/1. Отлично! Теперь осталось доказать, что перпендикуляр, опущенный из O на BCD, проходит через середину AH(где H - ортоцентр треугольника BCD). Для этого рассмотрим проекцию на BCD(пусть A" - проекция A, O1 - проекция O). Мы знаем, что проекция прямой AM проходит через точку пересечения медиан и центр описанной окружности. Что же это тогда за прямая?
Подсказка 5.
Да это же прямая Эйлера! А значит, она проходит и через ортоцентр треугольника BCD. Теперь, используя, что MH = 2MO1, попробуйте получить отношение отрезков A"O1 и O1H.
Подсказка 6.
Отлично! Мы знаем, что A"O1 = O1H. Тогда что можно сказать про отношение отрезков, на которые разбивается AH прямой OO1?
Проведём через пару скрещивающихся рёбер тетраэдра две параллельные плоскости. Так же поступим для двух других пар
скрещивающихся рёбер и получим параллелепипед. Диагонали его граней равны между собой, поэтому все грани — прямоугольники, и
параллелепипед прямоугольный. Пусть
— его центр, являющийся также центром описанной сферы тетраэдра
Пусть также
— точки, симметричные
соответственно относительно точки
Докажем, что все построенные прямые проходят
через точку
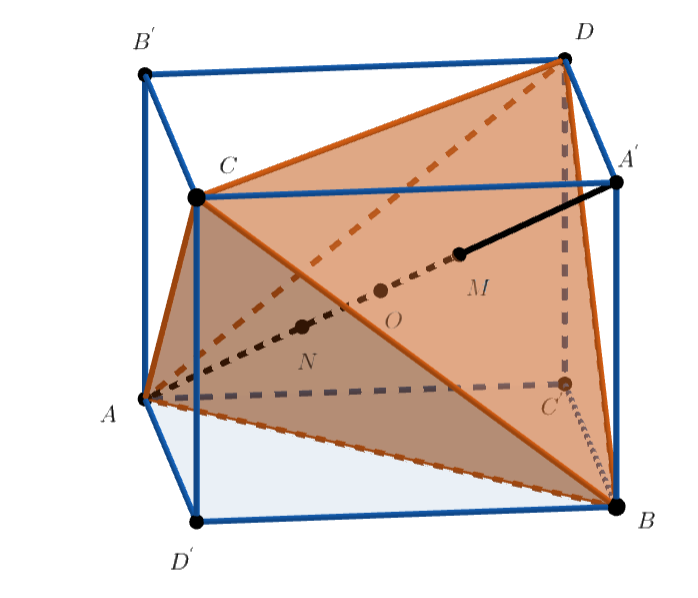
Пусть — центр масс треугольника
. Тогда
То есть точка лежит на диагонали
и делит её в отношении
, считая от вершины
Аналогично центр масс
треугольника
лежит на этой диагонали и делит её в отношении
, считая от вершины
Точка
— середина отрезка
поэтому
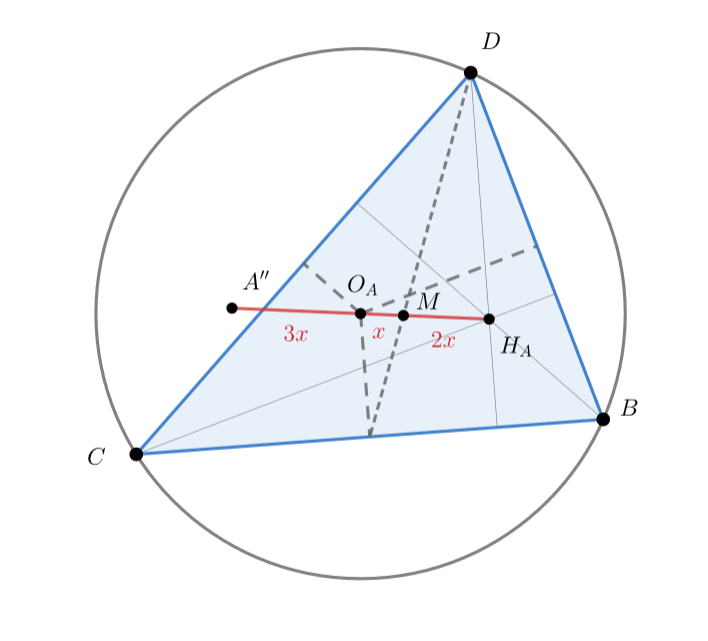
Рассмотрим проекцию на плоскость
— проекция точки
,
— проекция центра
Точка
совпадает с центром
описанной сферы тетраэдра
поэтому
— центр описанной окружности треугольника
Тогда прямая проецируется в прямую Эйлера
треугольника
Пусть
Тогда
(
делит
отрезок
в отношении
, это отношение сохраняется при проецировании). Кроме того,
лежат на одной прямой и
(прямая Эйлера), отсюда
Следовательно,
, а прямая
, перпендикулярная
плоскости
, делит отрезок
пополам, а значит, совпадает с прямой
. Итак, все построенные прямые проходят через точку
.
Ошибка.
Попробуйте повторить позже
Докажите, что сумма квадратов длин проекций ребер правильного тетраэдра на любую плоскость равна , где
— длина ребра
тетраэдра.
Подсказка 1
Наверное, мы понимаем, что работать с тетраэдром в этой задаче не очень удобно. К тому же непонятно, каким образом в такой конструкции считать квадраты проекций на любую плоскость... Но если нам попробовать получить более хорошую и знакомую и приятную фигуру? Подумайте, как это можно сделать.
Рассмотрим куб со стороной . Отметим у него две вершины на диагонали одной из граней (скажем, верхней грани) и две вершины
на диагонали параллельной (нижней) грани, непараллельной первой диагонали. Полученные
вершины образуют правильный тетраэдр со
стороной
, что и задано в условии. Теперь отметим, что проекция каждой грани куба — параллелограмм, в котором диагонали
равны проекциям рёбер тетраэдра. А по тождеству параллелограмма сумма квадратов диагоналей параллелограмма равна сумме
квадратов сторон, откуда следует равенство суммы квадратов проекций сторон тетраэдра аналогичной сумме для сторон
куба.
Итак, будем рассматривать куб. Пусть прямая , перпендикулярная плоскости, образует с рёбрами куба углы
. Тогда длины
проекций рёбер равны
. Заметим, что
— это длины перпендикуляров из вершины
единичного вектора (коллинеарного прямой
) на оси, то есть длины проекций вектора на координатные плоскости. Отсюда
сумма их квадратов равна единице. Из равенства для косинусов следует
. Поскольку каждая
проекция встречается ровно по
раза, то в итоге сумма длин проекций равна
, что и
требовалось.
что и требовалось доказать
Ошибка.
Попробуйте повторить позже
Пусть и
и
и
— длины пар противоположных рёбер тетраэдра;
соответственные углы между ними
Докажите, что одно из трёх чисел
и
— сумма двух других.
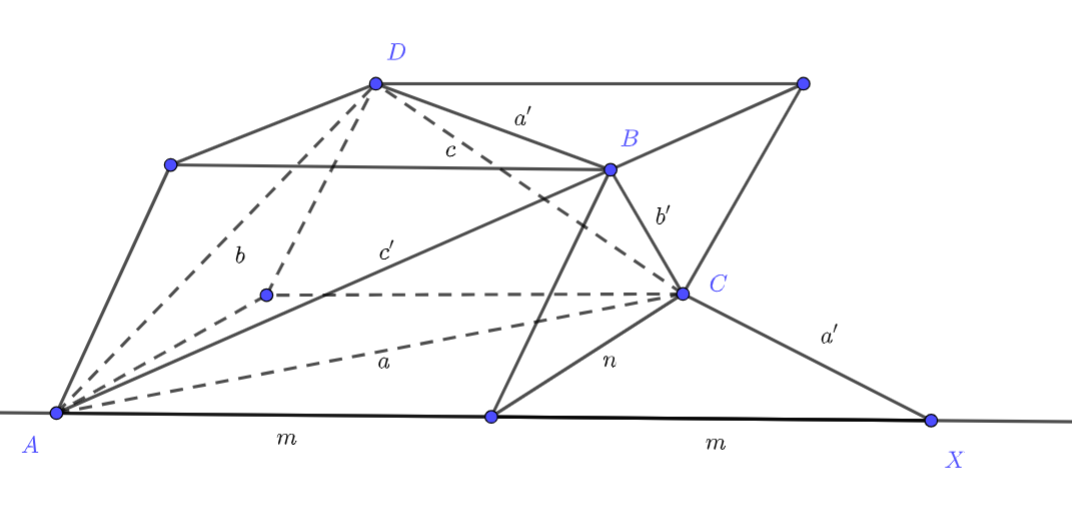
Достроим тетраэдр до параллелепипеда. Тогда и
- диагонали двух противоположных граней параллелепипеда. Пусть
и
-
стороны этих граней, причём
По теореме косинусов
и
поэтому
Записав такие равенства для чисел
и
получим требуемое.
Ошибка.
Попробуйте повторить позже
У Пети скопилось много кусочков пластилина трех цветов, и он плотно заполнил пластилином полый куб со стороной 5 см, так что в кубе не осталось свободного места. Докажите, что внутри куба найдутся две точки одного цвета на расстоянии ровно 7 см друг от друга.
Источники:
Подсказка 1
Казалось бы, из условия мы почти ничего не знаем, но нам известно количество цветов, а то, что нас просят доказать, намекает на принцип Дирихле. Подумайте, как его здесь применить.
В кубе рассмотрим 4 вершины
. Они являются вершинами правильного тетраэдра со стороной
, где
— ребро куба. Поскольку
, рассмотрим подобный тетраэдр с коэффициентом подобия
, т.е. проделаем гомотетию с
центром в центре куба и данным коэффициентом подобия. Получим четыре вершины нового тетраэдра внутри куба. Поскольку цветов у
пластилина три, хотя бы две вершины этого тетраэдра будут одного цвета.



