Развёртка
Ошибка.
Попробуйте повторить позже
Дан куб с ребром
. Точка
— центр грани
. Найдите наименьшее значение суммы длин
, если точка
лежит на отрезке
.
Подсказка 1
Нам нужно найти наименьшее значение суммы длин двух отрезков. Но... Они лежат вообще в разных плоскостях- это неудобно. Совсем непонятно, что делать с ними в таком виде. Когда есть неудобство, пробуем от него избавиться! Как это можно сделать?
Подсказка 2
Верно, мы же можем расположить их в одной плоскости. Уже ситуация полегче. Вспомним о том, что нам надо найти - наименьшую сумму длин. Обычно это делается с помощью неравенства. А какое самое простое неравенство есть для двух отрезков?
Подсказка 3
Да, это неравенство треугольника! Ведь по нему сумма двух сторон должна быть больше третьей. Хм... Но тогда же получается, что если Е попадёт на третью сторону, то это и будет минимум. Осталось только подумать, зачем нам дали такую хорошую точку О.
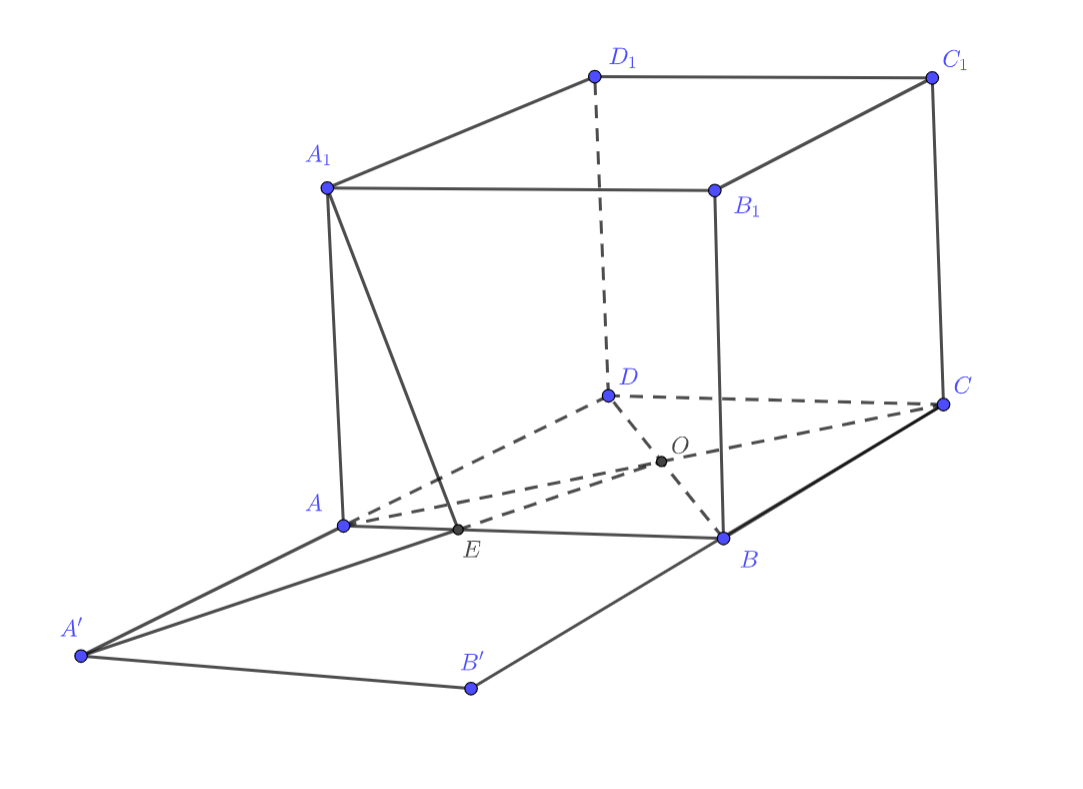
Рассмотрим и
. Тогда
для произвольной
(
получается
из
поворотом
на
относительно
). Но отсюда нам надо найти минимум
, который достигается только при
и будет равен
, то есть
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




