Развёртка
Ошибка.
Попробуйте повторить позже
На поверхности правильного тетраэдра построена замкнутая линия, каждая точка
которой обладает следующим свойством:
длина кратчайшего пути по поверхности тетраэдра между
и серединой ребра
равна длине кратчайшего пути по
поверхности тетраэдра между
и серединой ребра
. Найдите длину этой линии, если длина ребра тетраэдра равна
1.
Источники:
Подсказка 1
У нас тут рассматривается расстояние по поверхности...Как можно перевести картинку на плоскость в таком случае, чтобы было более удобно?
Подсказка 2
Рассмотреть развертку! Вот пусть мы развернули его так, что получился ромб ABCD, где AC - общее ребро у развернутых граней. Но все еще непонятно как работать с линиями ломаной, которые не получится нормально нарисовать на развертке. Что можно в таком случае придумать?
Подсказка 3
Давайте мысленно "порежем" нашу ломаную ребрами и отрезками AN, BN, CM, DM, где M и N - середины AB и CD, и рассмотрим только ту часть ломаной, что внутри треугольника AMC на нашей развертке. Наверное, в этом треугольнике не сложно найти такие точки на развертке?
Подсказка 4
Например, пусть P - точка ломаной внутри AMC. Понятно, что кратчайший путь от P до M - это PM, а кратчайший путь от P до N - это отрезок PN). Такие отрезки должны быть равны, а значит какое ГМТ у P?
Подсказка 5
Серединный перпендикуляр к MN! Достаточно легко теперь найти длину этой ломаной внутри AMC. А что делать с остальными частями этой ломаной? Вот что: попробуйте осознать, что они будут такими же, например, из соображений симметрии)
Пусть и
— середины ребер
и
соответственно. Из соображений симметрии ясно, что ребрами
и отрезками
линия, о которой идет речь в условии задачи разбивается на 8 равных. Поэтому достаточно рассмотреть точки,
принадлежащие треугольнику
.
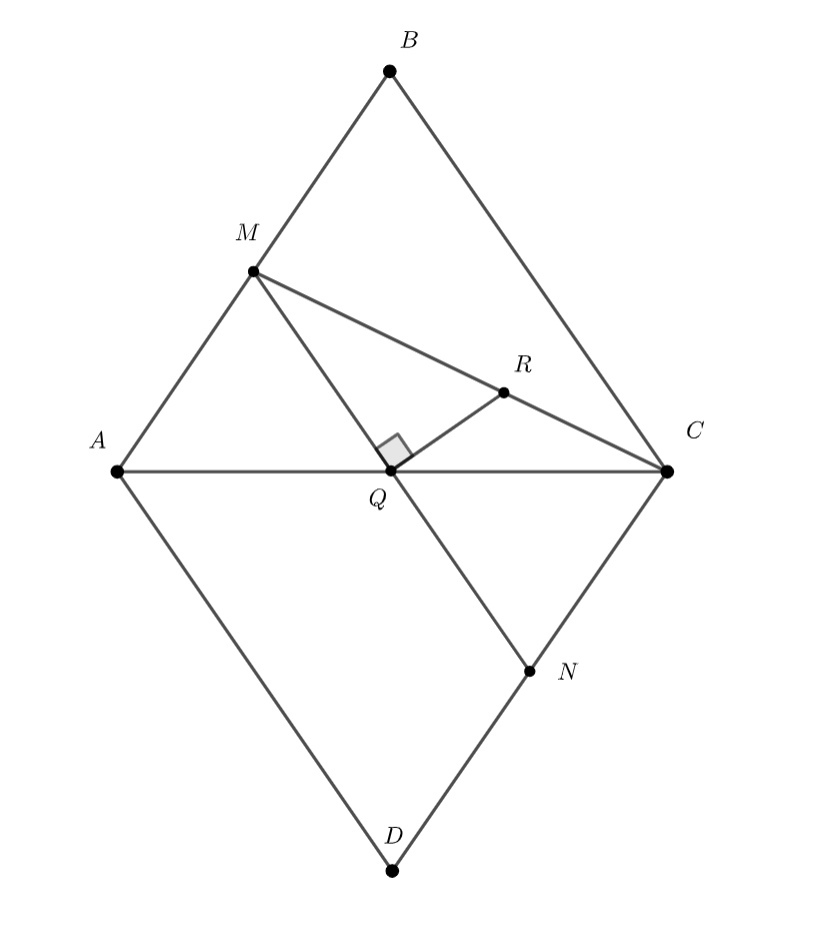
Пусть - одна из таких точек. Тогда кратчайшим путем между
и
служит отрезок
, а кратчайшим путем между
и
- двухзвенная ломаная
, вершина
которой принадлежит ребру
(в случае
имеем просто отрезок
. На развертке
тетраэдра объединение граней
и
представляет собой ромб
, а ломаная
- отрезок
в нем. Условие
означает, что
лежит на серединном перпендикуляре к отрезку
; следовательно геометрическим местом точек
служит отрезок
, где
- середина ребра
(и середина отрезка
)
- точка на отрезке
,
(см
рисунок).
Найдем длину отрезка . Легко видеть, что
, а отрезок
, будучи средней линией треугольника
, имеет длину
. Поэтому
Умножив это число на 8, получим ответ к задаче:
Ошибка.
Попробуйте повторить позже
На подвешенном воздухе кубике Рубика, на одном из его квадратиков, сидит жучок. В какой-то момент он начинает
движение по поверхности куба, передвигаясь за каждую секунду на соседний квадратик, т.е. на квадратик, имеющий общую
сторону с текущим. Соседний квадратик для первого перемещения был выбран произвольно, а затем жучок следовал таким
правилам:
1) при 2-м, 4-м и других чётных перемещениях жучок не менял направления своего движения, т.е. покидал квадратик через сторону, противоположную той, через которую он на этот квадратик попал;
2) при 3-м, 5-м и других нечётных перемещениях жучок поворачивал направо (относительно своего движения).
Через 2023 секунды после начала движения жучок обратил внимание на то, что уже был на этом же квадратике 5 секунд назад. Через какое наименьшее число секунд после 2023-й жучок опять окажется на этом квадратике?
Источники:
Подсказка 1
Заметим, что квадратиков ну ооочень много, но ведь многие из них очень похожи?… Если взять конкретный квадратик, то несложно отследить его путь, т.к путь у жучка определяется начальным положением и направлением. Что тогда попробуем сделать?
Для отслеживания движения жучка будем использовать частичную развертку куба, покрывающую грани. Каждый квадратик будем
обозначать двузначным числом, 1-я и 2-я цифры которого являются соответствующими координатами центра квадратика на развертке
(единица — ширина квадратика):

Маршрут жучка определяется его начальным положением и направлением его первого перемещения. Хотя всего таких вариантов
их все можно разбить на
принципиально различных групп:
1) Жучок стартует с центрального квадратика любой грани по направлению к любому ребру
2-3) Старт с углового квадратика любой грани, а первое перемещение в пределах той же грани вдоль ребра, идущего соответственно справа или слева от жучка
4-5) Старт с углового квадратика любой грани, а при первом перемещении жучок переползает на соседнюю грань, причем третья примыкающая грань остается соответственно справа или слева от него
6) Старт с приреберного квадратика любой грани по направлению к центру
7) Старт с приреберного квадратика любой грани с переходом на соседнюю грань при первом перемещении
8-9) Старт с приреберного квадратика любой грани, а первое перемещение в пределах той же грани вдоль ребра, идущего соответственно справа или слева от жучка
Заполним таблицу, в которой для каждой группы приведем пример маршрута в течение того времени, когда обнаруживается его
периодичность, т.е. когда на какой-либо четной секунде жучок оказывается на начальном квадратике, а еще через с — на квадратике, где
он был через
с после начала движения.
В случае группы выберем для старта квадратик
с первым перемещением
и проследим весь маршрут, пока не обнаружим,
что его период равен
c (1-я колонка таблицы после двойной вертикальной черты).
Заметим, что через c после начала движения жучок окажется в начальном состоянии группы
Поэтому для нее маршрут также
будет иметь период
с и его можно получить из маршрута группы
сдвигом на
с.
Еще через с жучок окажется в начальном состоянии группы
Поэтому и для нее маршрут будет с периодом
с и его можно
получить из маршрута группы
сдвигом на
с.
Еще через с имеем начальное состояние группы
и получаем ее маршрут с периодом
с из маршрута группы
сдвигом на
с.
Для остальных групп получаются кольцевые маршруты с периодом с, причем в течение одного периода жучок ни на одном
квадратике не оказывается дважды.
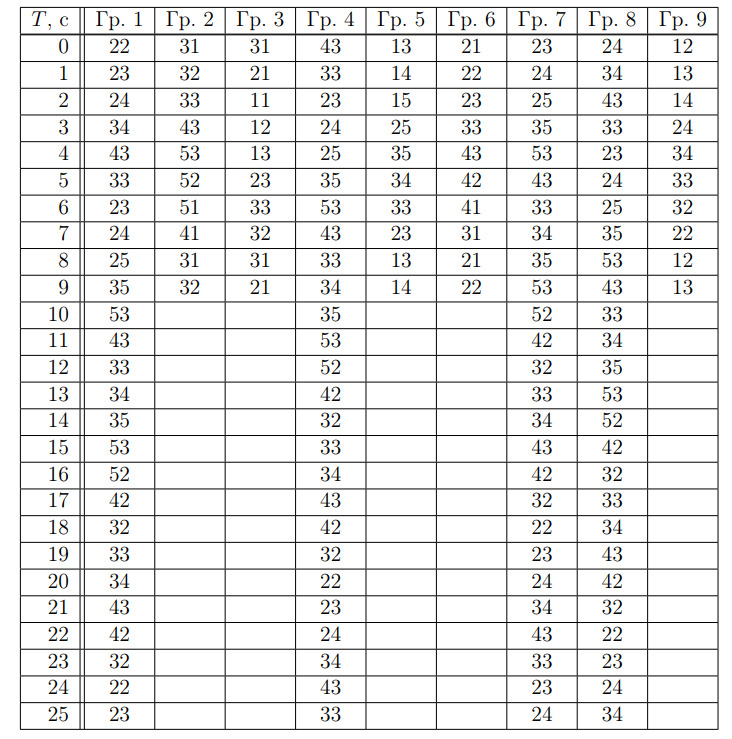
Так как (остаток от деления
на
равен
) и
(остаток от деления
на
равен
то через
с после начала движения жучок окажется на том же
квадратике, на котором он был через
с после начала, а за
с до этого — на том же квадратике, на котором он был через
с после
начала.
Как видно из таблицы, такое совпадение имеет место только для группы (квадратик
Так как этот квадратик встречается на
маршруте только дважды в течение периода (
с и
с), следующее попадание на него произойдет через
(с).
Ошибка.
Попробуйте повторить позже
Дан куб с ребром
. Точка
— центр грани
. Найдите наименьшее значение суммы длин
, если точка
лежит на отрезке
.
Подсказка 1
Нам нужно найти наименьшее значение суммы длин двух отрезков. Но... Они лежат вообще в разных плоскостях- это неудобно. Совсем непонятно, что делать с ними в таком виде. Когда есть неудобство, пробуем от него избавиться! Как это можно сделать?
Подсказка 2
Верно, мы же можем расположить их в одной плоскости. Уже ситуация полегче. Вспомним о том, что нам надо найти - наименьшую сумму длин. Обычно это делается с помощью неравенства. А какое самое простое неравенство есть для двух отрезков?
Подсказка 3
Да, это неравенство треугольника! Ведь по нему сумма двух сторон должна быть больше третьей. Хм... Но тогда же получается, что если Е попадёт на третью сторону, то это и будет минимум. Осталось только подумать, зачем нам дали такую хорошую точку О.
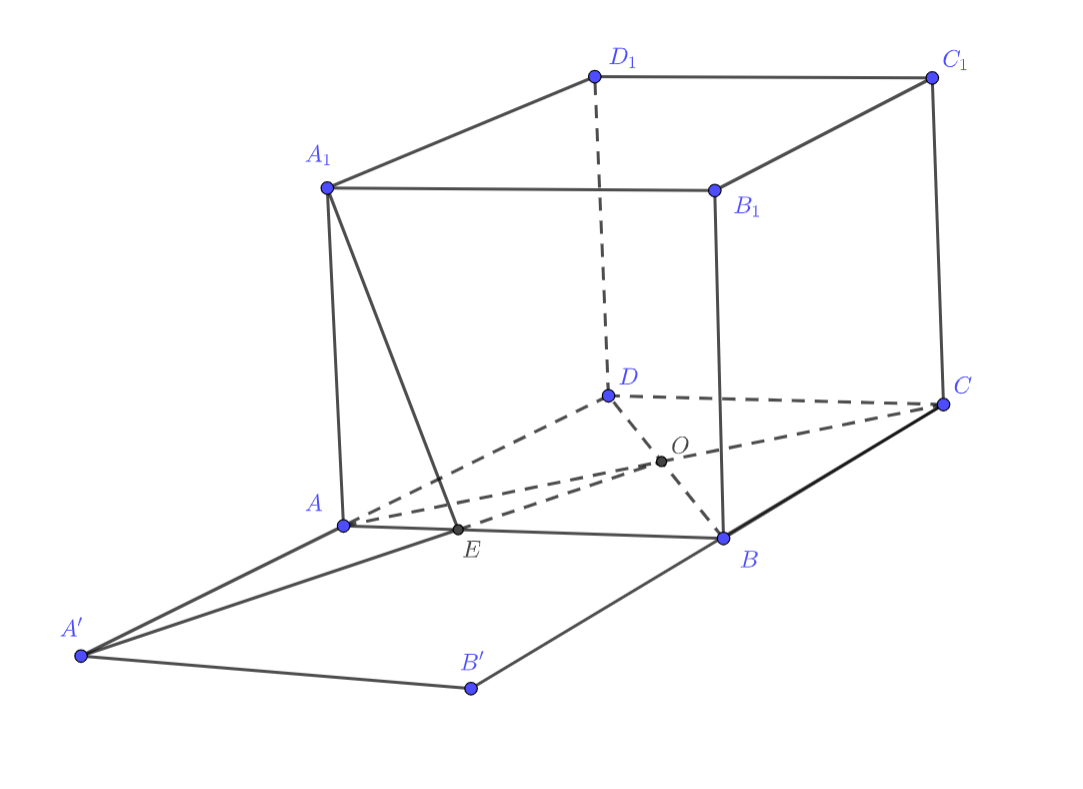
Рассмотрим и
. Тогда
для произвольной
(
получается
из
поворотом
на
относительно
). Но отсюда нам надо найти минимум
, который достигается только при
и будет равен
, то есть
Ошибка.
Попробуйте повторить позже
Выберите кубик, соответствующий данной развертке.

В ответ укажите одну строчную букву.
Отметим на развертке точки, которые склеются при сборке кубика, одним цветом, а так же перенумеруем грани.
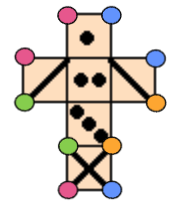
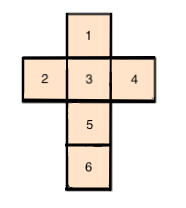
Как видно, красная вершина — вершина принадлежащая ,
и
граней, — а так же синяя вершина — вершина принадлежащая
,
и
граней, — не являются концами отрезков, нарисованных на второй и четвертых гранях, а значит картинка (а) не соответствует этой
развертке.
Также не являются концами отрезков, нарисованных на второй и четвертых гранях, вершины, принадлежащие и
граням, а значит
кубик (б) имеет другую развертку.
На пятой грани три точки соответствуют диагонали, один из концов которой — оранжевая вершина. Значит, на рисунке (г) спереди сверху изображена зеленая вершина. Зеленая вершина находится слева от грани 6 на развертке, но справа на рисунке кубика, а занчит, этот кубик не соответсвует этой развертке.
Остается кубик под буквой (в).
Ошибка.
Попробуйте повторить позже
Дан куб с ребром длины
. На середине ребра
взята точка
, а на ребре
на расстоянии
от вершины
взята точка
Найти длину кратчайшего пути между точками
и
по поверхности куба.
Минимизируем длину пути с помощью развёртки куба. По неравенству ломаной сумма длин отрезков будет минимальна, если их концы лежат на одной прямой.
Если путь идёт только по ,
и
, то длина по этим двум граням будет
. Если путь идёт только
по
и
, то длина по этим двум граням будет
. Аналогично по граням
,
и
или
и
, а других вариантов нет.
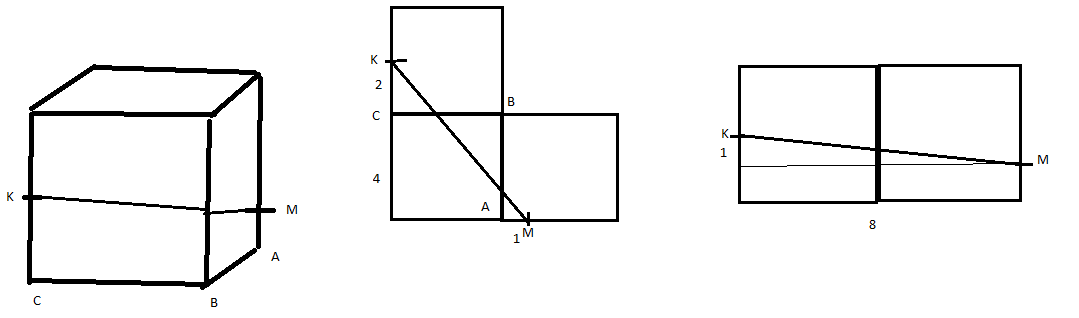
Ошибка.
Попробуйте повторить позже
В неправильной пирамиде сумма плоских углов при вершине
равна
. Найдите площадь поверхности этой пирамиды, если
площадь грани
равна
и
Источники:
Подсказка 1
Дана пирамида и некие условия на неё, которые касаются углов и сторон. А вычислить нужно площадь поверхности, то есть "плоскую" характеристику. Что тогда можно сделать, чтобы упростить себе восприятие задачи?
Подсказка 2
Естественное желание при решении почти любой стереометрической задачи — свести её к задаче по планиметрии. Здесь, поскольку речь идёт о сторонах, плоских углах и площадях, будет удобно рассмотреть развёртку пирамиды. Воспользуемся же всеми условиями задачи на развёртке!
Подсказка 3
Теперь наглядно можно увидеть, что мы имеем 4 треугольника, кучу равных отрезков и 3 угла при вершине А, составляющие в сумме развёрнутый. Что хочется доказать про эти треугольники?
Подсказка 4
Конечно, хочется доказать, что все 4 треугольника равны между собой. Воспользуемся признаками равенства треугольников и параллельностью!
Докажем, что грани пирамиды — равные треугольники. Для этого рассмотрим развёртку пирамиды
,
где
![]()
Пусть . Так как
, то точки
лежат на одной прямой. Так как
, то
— параллелограмм и
. Аналогично
— тоже параллелограмм. Треугольник
равен треугольнику
. Значит, грани пирамиды — равные треугольники.


