Развёртка
Ошибка.
Попробуйте повторить позже
На поверхности правильного тетраэдра построена замкнутая линия, каждая точка
которой обладает следующим свойством:
длина кратчайшего пути по поверхности тетраэдра между
и серединой ребра
равна длине кратчайшего пути по
поверхности тетраэдра между
и серединой ребра
. Найдите длину этой линии, если длина ребра тетраэдра равна
1.
Источники:
Подсказка 1
У нас тут рассматривается расстояние по поверхности...Как можно перевести картинку на плоскость в таком случае, чтобы было более удобно?
Подсказка 2
Рассмотреть развертку! Вот пусть мы развернули его так, что получился ромб ABCD, где AC - общее ребро у развернутых граней. Но все еще непонятно как работать с линиями ломаной, которые не получится нормально нарисовать на развертке. Что можно в таком случае придумать?
Подсказка 3
Давайте мысленно "порежем" нашу ломаную ребрами и отрезками AN, BN, CM, DM, где M и N - середины AB и CD, и рассмотрим только ту часть ломаной, что внутри треугольника AMC на нашей развертке. Наверное, в этом треугольнике не сложно найти такие точки на развертке?
Подсказка 4
Например, пусть P - точка ломаной внутри AMC. Понятно, что кратчайший путь от P до M - это PM, а кратчайший путь от P до N - это отрезок PN). Такие отрезки должны быть равны, а значит какое ГМТ у P?
Подсказка 5
Серединный перпендикуляр к MN! Достаточно легко теперь найти длину этой ломаной внутри AMC. А что делать с остальными частями этой ломаной? Вот что: попробуйте осознать, что они будут такими же, например, из соображений симметрии)
Пусть и
— середины ребер
и
соответственно. Из соображений симметрии ясно, что ребрами
и отрезками
линия, о которой идет речь в условии задачи разбивается на 8 равных. Поэтому достаточно рассмотреть точки,
принадлежащие треугольнику
.
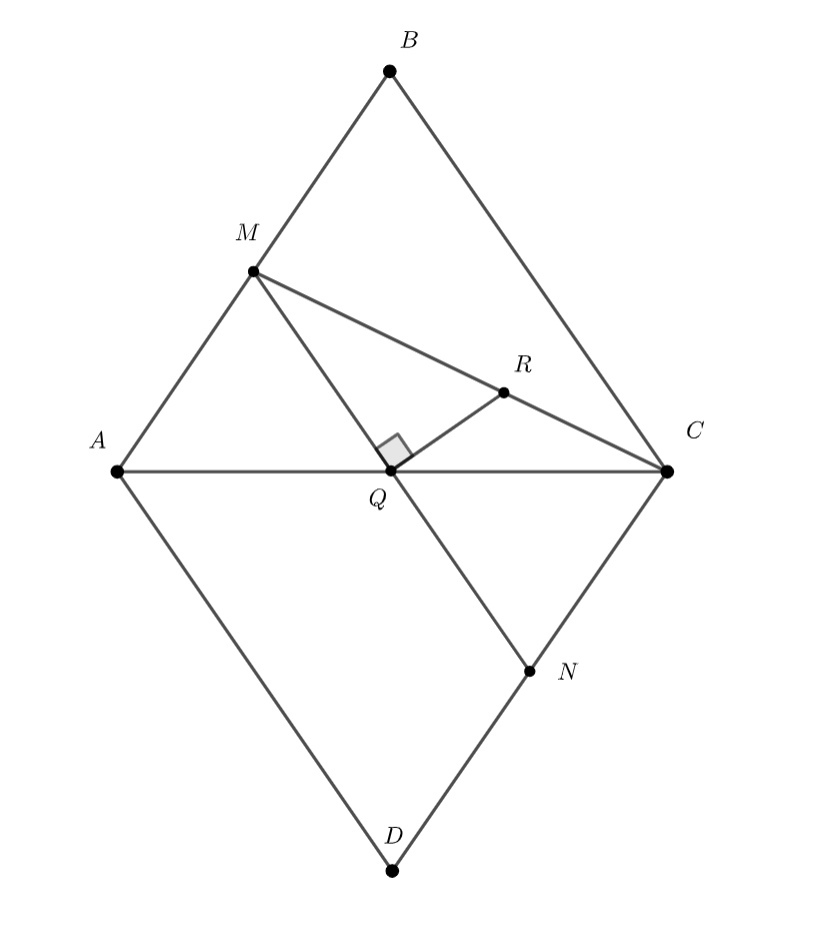
Пусть - одна из таких точек. Тогда кратчайшим путем между
и
служит отрезок
, а кратчайшим путем между
и
- двухзвенная ломаная
, вершина
которой принадлежит ребру
(в случае
имеем просто отрезок
. На развертке
тетраэдра объединение граней
и
представляет собой ромб
, а ломаная
- отрезок
в нем. Условие
означает, что
лежит на серединном перпендикуляре к отрезку
; следовательно геометрическим местом точек
служит отрезок
, где
- середина ребра
(и середина отрезка
)
- точка на отрезке
,
(см
рисунок).
Найдем длину отрезка . Легко видеть, что
, а отрезок
, будучи средней линией треугольника
, имеет длину
. Поэтому
Умножив это число на 8, получим ответ к задаче:
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




