Изогональное сопряжение

Первое решение. Обозначим треугольник, образованный синими лучами, через (как на рисунке), и пусть его описанная окружность касается окружности Пусть окружность вторично пересекает окружность в точке (которая, очевидно, лежит внутри треугольника ). Тогда и Поскольку также

(второе равенство — сумма внешних углов треугольника ), то Таким образом, точка лежит и на окружности

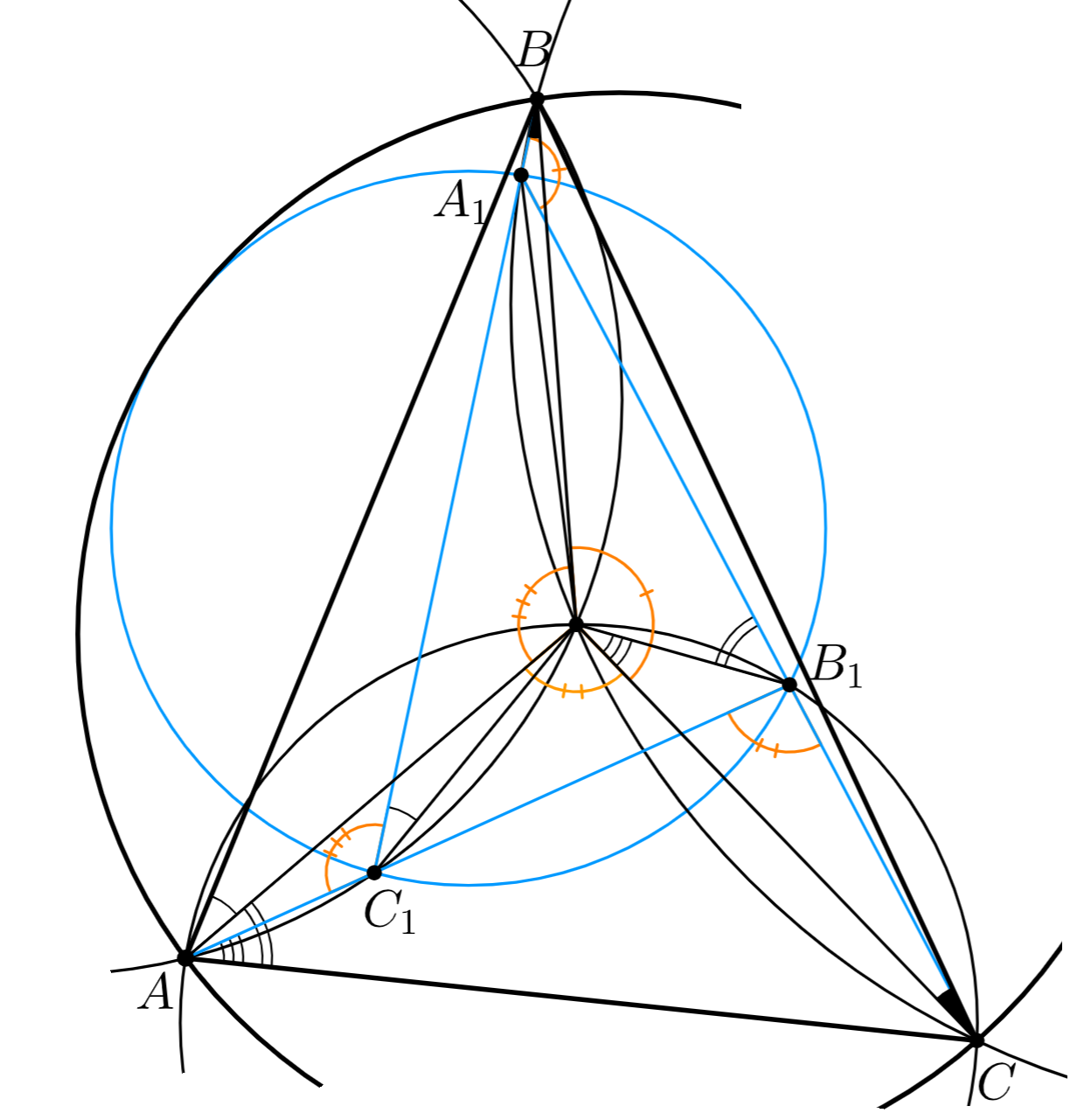
Сделаем инверсию с центром в точке (и с произвольным радиусом), образы точек будем обозначать теми же буквами со штрихами. Напомним, что для любых точек и треугольники и подобны (по углу и отношению заключающих сторон), поэтому

Докажем, что треугольник подобен треугольнику Действительно,

аналогично для остальных углов.

Окружность при инверсии перейдет в прямую проходящую через вершину треугольника Найдем угол между этой прямой и стороной

Вместе с двумя аналогичными равенствами отсюда следует, что в подобных треугольниках и красные лучи в первом и лучи во втором — соответствующие элементы. Окружности и касаются (поскольку они получены инверсией из касающихся окружностей), а тогда и окружность касается описанной окружности треугольника, ограниченного красными лучами, что и требовалось.

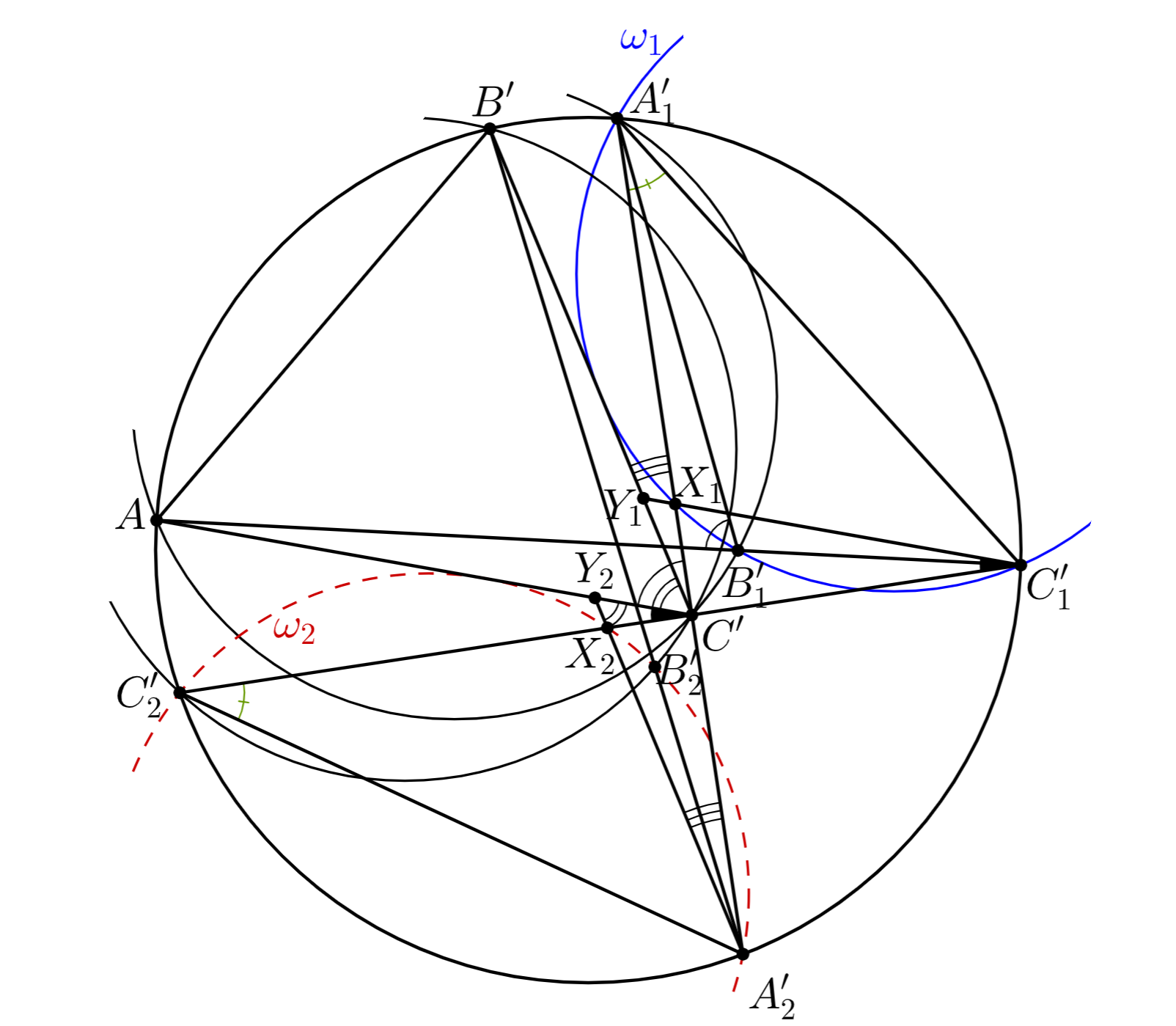
Второе решение. Обозначим треугольник, образованный красными лучами, через а треугольник, образованный синими — (обозначения введем как на рисунке). Для определенности будем считать, что именно окружность касается окружности а доказать нужно то же про окружность

Без ограничения общности можно считать, что точка лежит на отрезке По условию и Следовательно, точки и изогонально сопряжены относительно треугольника Аналогично, изогонально сопряжены точки и и

Обозначим через композицию инверсии с центром в точке с радиусом и симметрии относительно биссектрисы угла Тогда преобразование меняет местами точки и Образы точек и нам поможет описать следующее вспомогательное утверждение.

_________________________________________________________________________________________________________________________________________________________________________________

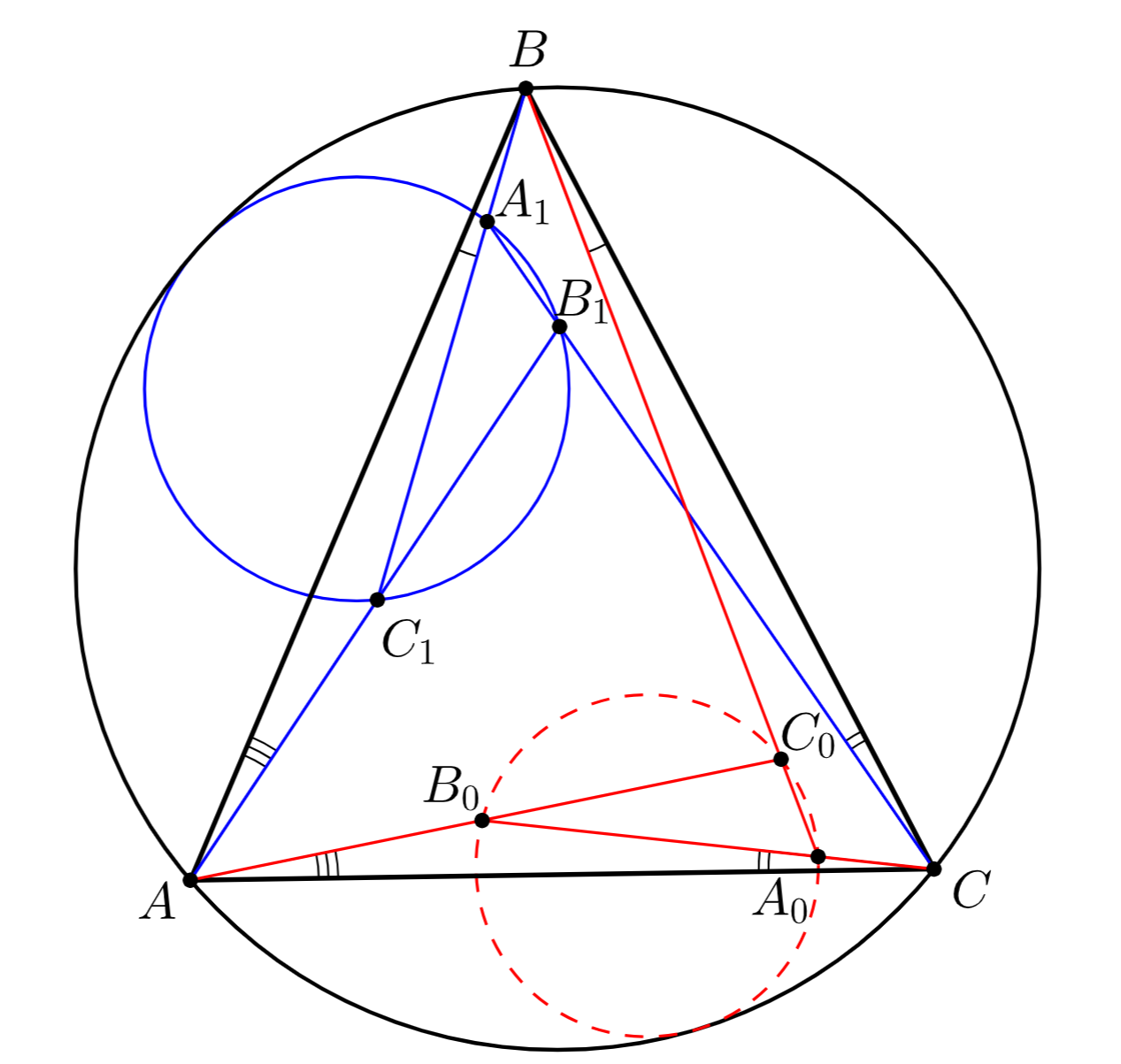
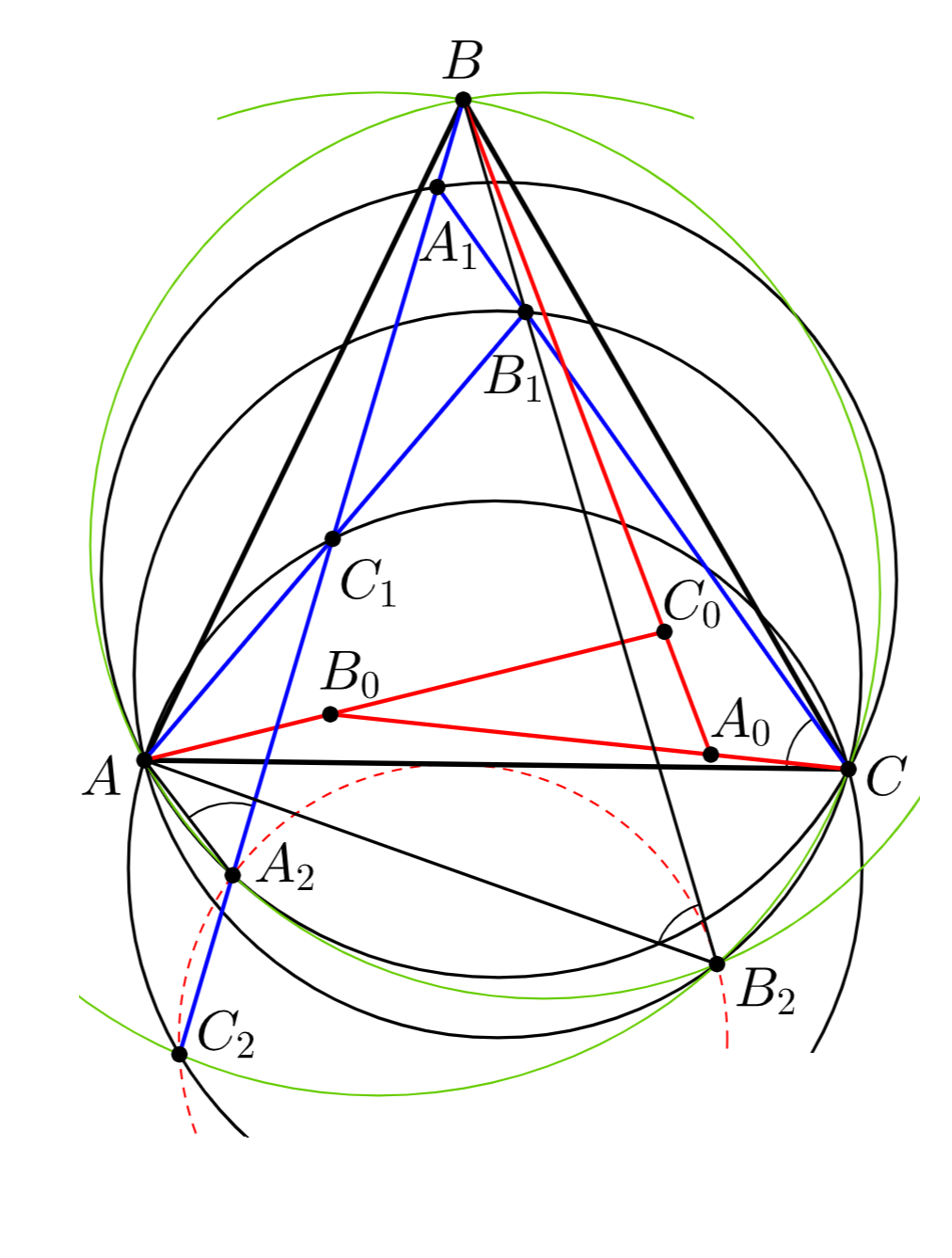
Лемма. Пусть точки и изготовлено сопряжением относительно треугольника Пусть прямая вторично пересекает окружность, описанную около треугольника в точке Тогда

Доказательство. Пусть Поскольку то треугольники и подобны, в частности, откуда следует, что точка лежит на продолжении отрезка за точку А также

поэтому точка лежит на окружности Значит, лемма доказана.

___________________________________________________________________________________

Вернёмся к решению задачи. Пусть прямая вторично пересекает окружность в точке прямая окружность — в точке прямая окружность — в точке Тогда, согласно лемме, Кроме того, переводит окружность в прямую Следовательно, достаточно доказать, что прямая касается окружности

В силу вписанности четырёхугольников и мы получаем, что

поэтому четырёхугольник вписанный. Аналогично четырёхугольник тоже вписанный.

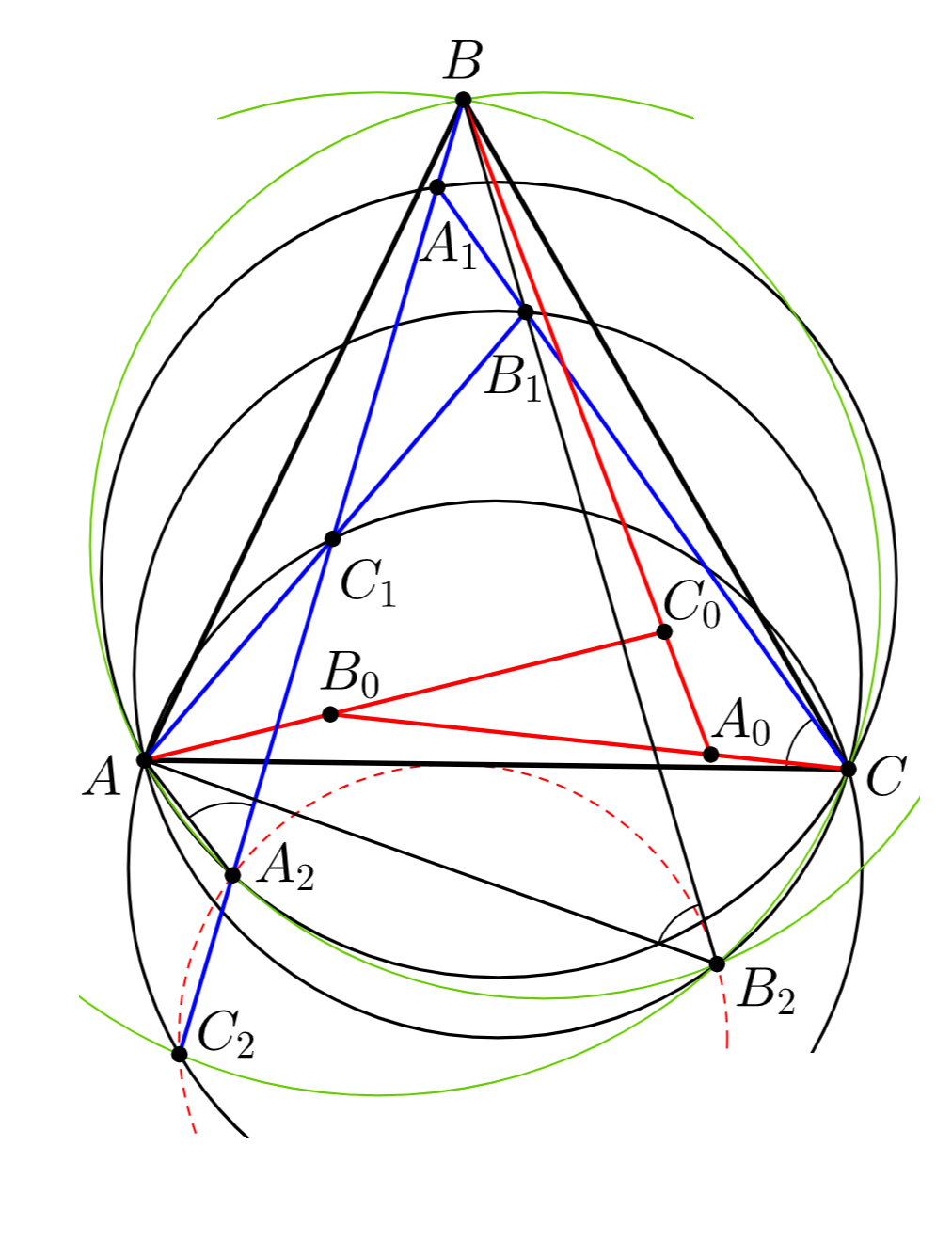
Сделаем инверсию с центром в точке (и произвольным радиусом). Образы точек будем обозначать теми же буквами со штрихами.

Поскольку точка лежит на отрезке то точка лежит на продолжении отрезка при этом и точка и точка расположены в угле но вне треугольника Точка лежит внутри угла и вне треугольника Поскольку точки лежат на одной прямой, точка лежит на окружности В частности, она расположена внутри угла

Точки расположены в другой полуплоскости относительно прямой нежели точка Кроме того, поскольку четырёхугольники и вписанные, то точка лежит на отрезках а точка — на отрезке Поскольку окружности и касаются, то окружность обозначим ее через касается прямой Также четырёхугольники и шестиугольник все вписанные, поскольку точка точка лежит на отрезке четырёхугольник вписанный, а также точки лежат на одной прямой именно в таком порядке.

Теперь достаточно доказать, что окружность обозначим ее через касается прямой потому что это означает, что до инверсии касались окружности и

Проведем через точку прямую параллельно и обозначим ее точки пересечения с прямыми и через и соответственно. Через точку проведем прямую параллельно и обозначим ее точки пересечения с прямыми и через и соответственно.

Четырёхугольник вписанный, а также Значит,

Следовательно, точка лежит на окружности Аналогично точка лежит на

Пусть — полуплоскость, ограниченная прямой в которой лежит точка Аналогично — полуплоскость, в которой лежит точка ограниченная прямой Обозначим через преобразование подобия, которое переводит точку в точку точку в точку а также полуплоскость в полуплоскость (Такое преобразование подобия можно получить, например, как композицию поворотной гомотетии, переводящей в и в и симметрии относительно прямой )

Четырёхугольник вписанный, поэтому Следовательно, преобразование переводит окружность в окружность Далее мы докажем, что, во—первых,

и, во—вторых,

Отсюда последует, что переводит точку в точку а также прямую в прямую Таким образом, поскольку прямая касается окружности то прямая касается окружности что и требовалось.

Остается доказать соотношения () и (). В силу параллельности и а также и имеем, что

откуда следует (). Кроме того, и поэтому треугольник подобен треугольнику по двум углам, а треугольник — треугольнику Следовательно, и Разделив первое полученное равенство на второе, мы получаем в точности соотношение ().

Отметим, что точки и могут располагаться на продолжениях отрезков и (за точки и ), но на решение это не влияет.