.01 Банк ФИПИ
Ошибка.
Попробуйте повторить позже
В 1828 г. английский ботаник Роберт Броун заметил, что взвешенные в воде мельчайшие частицы вещества находятся в непрерывном движении. Они то удаляются, то приближаются друг к другу, то поднимаются вверх, то опускаются вниз. Обнаруженное учёным движение взвешенных частиц стало называться броуновским движением.
В конце XIX в. исследование броуновского движения приобрело огромное теоретическое значение и привлекло внимание многих физиков-теоретиков. В рамках сформировавшихся к тому времени представлений о молекулярном строении вещества это движение получило вполне логичное объяснение: броуновская частица движется благодаря нескомпенсированным ударам со стороны непрерывно движущихся молекул жидкости. Однако никаких прямых измерений скорости движения молекул на тот момент времени не существовало.
В 1920 г. Отто Штерн провел опыты по исследованию средней скорости движения молекул. Устройство прибора Штерна схематично представлено на рисунке 1.

Рисунок 1. Схема опыта Штерна
Прибор состоял из двух расположенных вертикально цилиндров радиусом r и R, пространство внутри которых непрерывно откачивалось до очень низкого давления. По общей оси 1 цилиндров располагалась платиновая нить, покрытая тонким слоем серебра. При пропускании по платиновой нити электрического тока она нагревалась до высокой температуры. Серебро начинало испаряться, и его атомы разлетались, равномерно оседая на внутренней поверхности малого цилиндра. Щель 2
в стенке малого цилиндра выделяла узкий пучок молекул, которые долетали до внутренней поверхности большого цилиндра и «прилипали» к ней, образуя налёт серебра в виде узкой вертикальной полоски N.
Если весь прибор приводился в быстрое вращение с угловой скоростью ω, то налёт серебра смещался и давал более размытую полоску M шириной х.
Длина ρ дуги МN равна пути, проходимому точками большого цилиндра за время t полёта молекулы от щели до стенки большого цилиндра. Если обозначить через u скорость движения точек большого цилиндра, то получим уравнение, из которого можно определить скорость движения молекул v:
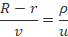
На рисунке 2 представлены экспериментальные данные по толщине осевшего слоя молекул, измеренные в различных точках в
пределах ширины
полоски
.
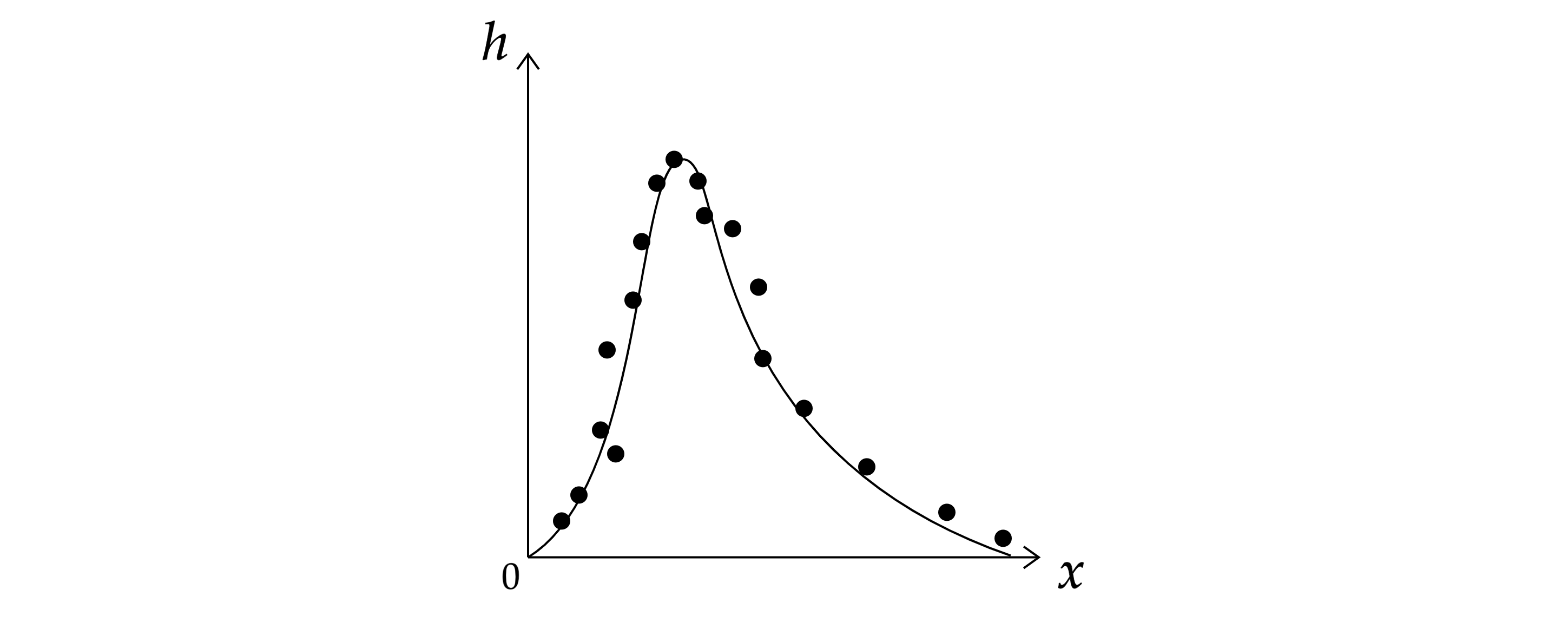
Рисунок 2
Можно ли на основании проведённого исследования утверждать, что при заданной температуре все молекулы серебра движутся с
одинаковой по модулю скоростью? Ответ поясните.
Источники:
Если бы все молекулы серебра двигались с одной и той же скоростью, то они бы прилетали в одну и ту же точку на стенке
цилиндра. В этом случае серебро осело бы в виде очень узкой, чёткой полоски, и график (толщина слоя в зависимости от
положения) имел бы один резкий пик.
Но на графике видно, что:
серебро осело в виде широкой полоски; толщина слоя меняется по положению
и плавно убывает — это значит, что молекулы
прилетали в разные точки.
Это возможно только если молекулы имели разные скорости. Быстрые молекулы долетают раньше и дальше, медленные — позже и
ближе.
| Критерии оценивания выполнения задачи | Баллы |
| Представлен правильный ответ на вопрос, и приведено достаточное обоснование, не содержащее ошибок | 2 |
| Представлен правильный ответ на поставленный вопрос, но его обоснование не является достаточным, хотя содержит указание на физические явления (законы), причастные к обсуждаемому вопросу. | 1 |
|
ИЛИ
| |
| Представлены корректные рассуждения, приводящие к правильному ответу, но ответ явно не сформулирован | |
| Представлены общие рассуждения, не относящиеся к ответу на поставленный вопрос. | 0 |
|
ИЛИ
| |
| Ответ на вопрос неверен, независимо от того, что рассуждения правильны, или неверны, или отсутствуют. | |
| Максимальный балл | 2 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




