.04 Антикайфовый процесс
Ошибка.
Попробуйте повторить позже
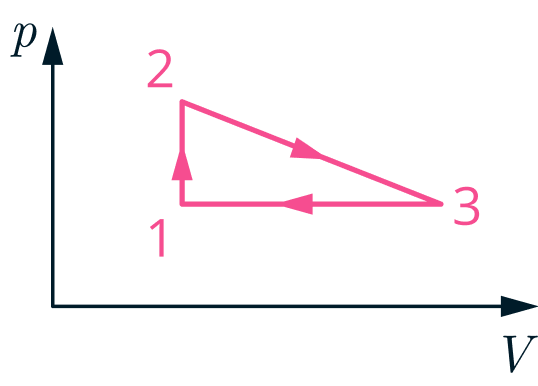
С молями идеального газа проводят циклический процесс 1-2-3-1, состоящий из: (а) изохорического нагревания 1-2, (б)
участка 2-3 с линейной зависимостью давления от объема, (в) изобарического сжатия 1-3 (см. рисунок). Известно, что
отношение максимального и минимального объемов газа в течение цикла равно 3 , отношение максимального и
минимального давлений газа в течение цикла равно 2 , максимальная разность температур в течение всего цикла -
.
Найти работу газа за цикл.
(Росатом 2025, 10)
Источники:
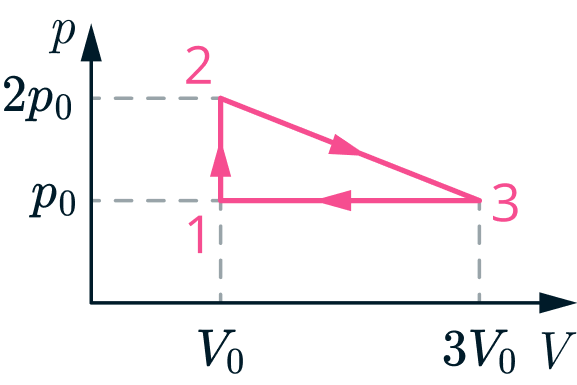
Пусть давление и объем газа в состоянии 1 равны и
. Поскольку это минимальные значения давления и объема в
цикле, то давление газа в состоянии 2 есть
, а объем в состоянии 3 есть
(см. рисунок). Так как работа
газа в циклическом процессе - это площадь цикла в координатах «давление-объем», то работа газа в нашем
процессе:
Теперь нужно выразить через данное в условии максимальное изменение температуры газа. Очевидно,
минимальной будет температура газа в состоянии 1 (т.к. в этом состоянии самым малым среди всех состояний цикла
является произведение давления на объем, которое связано законом КлапейронаМенделеева с температурой газа). Эту
величину легко найдем из закона Клапейрона-Менделеева:
А вот максимальной является температура какого-то состояния на участке 2-3. Найдем это состояние и максимальную температуру.
Зависимость давления от объема на участке 2-3 задается соотношением:
(можно непосредственной подстановкой проверить, что этому уравнению удовлетворяют две точки, лежащие на прямой
2-3: и (
). Подставляя эту зависимость в закон Клапейрона-Менделеева
получим зависимость температуры газа от его объема:
Математически эта зависимость представляет собой параболу с ветвями, направленными вниз, и обращающуюся в нуль
при и
. Поэтому эта функция достигает максимума посередине между этими точками.
Т.е.
Следовательно, максимальное изменение температуры газа в рассматриваемом процессе можно найти как
Отсюда получаем окончательное выражение для работы газа:
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




