Счётная планиметрия
Ошибка.
Попробуйте повторить позже
В неравнобедренном треугольнике серединные перпендикуляры к сторонам
и
пересекают высоту из вершины
в точках
и
соответственно. Найдите радиус описанной около этого треугольника окружности, если
Источники:
Пусть для определенности углы — острые, обозначим
. Так как
— высота, то
Пусть
— середины
соответственно.
Первое решение.
![]()
Отметим точку пересечения серединных перпендикуляров
и
к сторонам треугольника
. Эта точка является центром
описанной около треугольника окружности. Заметим, что угол
вдвое меньше центрального угла
поэтому равен
вписанному углу
то есть
При этом
из вписанности четырёхугольника
(два прямых угла
дают вписанность). Тогда обратим внимание, что
касается описанной окружности треугольника
, так как угол
между ней и хордой
равен углу
опирающемуся на эту хорду. По теореме о касательной и секущей получаем
Второе решение.
![]()
Не будем думать и посчитаем в синусах: из прямоугольных треугольников
Тогда получается
Наконец, по теореме синусов радиус описанной окружности равен
Ошибка.
Попробуйте повторить позже
Окружность с центром в точке
на стороне
треугольника
касается сторон
и
в точках
и
соответственно.
Известно, что
, а угол
равен
. Найти углы треугольника
и отношение его площади к площади круга,
ограниченного окружностью
Подсказка 1
Давайте будем думать, как нам считать и что через что выражается. Сразу понятно, что если нам дан угол EOD, то и угол B нам также дан. При этом, если у нас были бы известны углы C и A, то крайне понятно считались бы оба прямоугольных треугольника AOD и COE. Что нам это дает, для нахождения углов? Как мы можем их между собой связать?
Подсказка 2
Мы могли бы связать углы A и С, так как в прямоугольных треугольниках две стороны равны как радиусы, а отношение двух других равно константе. При этом, есть еще одна связь, что сумма углов A и С равна заданному углу DOE. Значит, мы найдем углы A и C. Как теперь можно найти отношение площадей круга и треугольника, если уже известны углы, а значит и радиус и стороны треугольника ABC?
Подсказка 3
Верно, к примеру, мы можем расписать через sin(DOE/2) и cos(DOE/2) отрезок DE, так как треугольник DOE - равнобедренный(т.синусов и опустить высоту, к-ая будет и медианой). Значит, мы через известный нам котангенс, выразим котангенс от половины такого же угла, а после этого сможем явно написать чему равны отрезки BD, BE и OE(последнее - радиус), а значит, найдем окружность. Правда ли, что теперь у нас осталось выразить только отрезки CE и AD и площадь треугольника также будет найдена?
Подсказка 4
Ну конечно, ведь тогда мы найдем обе стороны нашего треугольника и угол между ними. А значит и площадь. Как их найти? Так у нас же есть радиус и углы в прямоугольных треугольниках. Значит, мы сможем, все что нужно найти. Остается только посчитать :)
![]()
Обозначим
Так как , то
Из прямоугольных
и
находим
Так как и
— радиус окружности
Так как , то получаем
, т. е.
Так как угол острый как угол прямоугольного
Из равнобедренных и
находим
Отсюда
Тогда площадь равна
И искомое отношение равно
Ошибка.
Попробуйте повторить позже
Внутри треугольника отмечена точка
так, что
Прямая
пересекает сторону
в точке
Оказалось, что
Докажите, что
Отметим на отрезке такую точку
что
![]()
Тогда равенство из условия задачи можно записать в виде
откуда и треугольники
и
подобны. Но треугольники
и
равны, значит,
значит,
треугольник
равнобедренный, а вместе с ним и треугольник
равнобедренный.
Ошибка.
Попробуйте повторить позже
Пусть — биссектриса треугольника
точки
— центры вписанных окружностей треугольников
и
соответственно. Прямая
пересекает прямую
в точке
Докажите, что
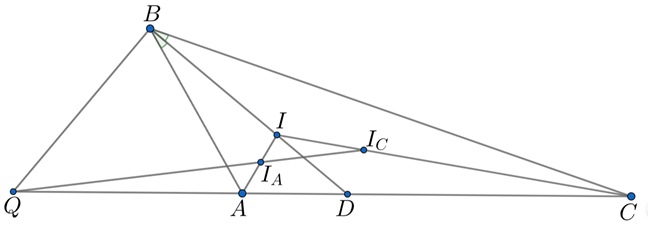
Прямые и
пересекаются в центре
вписанной окружности треугольника
При этом
По теореме
Менелая
Следовательно, — внешняя биссектриса угла
что и требовалось.
Ошибка.
Попробуйте повторить позже
В треугольнике в котором
точка
на стороне
такова, что
Точка
— середина
точки
на
стороне
и
на луче
таковы, что точки
и
лежат на одной прямой, которая параллельна
Докажите, что
Пусть — точка, симметричная точке
относительно
В четырехугольнике
диагонали пересекаются в точке
и делятся
точкой пересечения пополам, следовательно
является параллелограммом, в частности прямые
и
параллельны. Пусть
— точка, пересечения прямых
и
тогда
так же является параллелограммом, таким образом,
Аналогично,
И
Докажем, что Действительно, из подобия треугольников
и
следует равенство отношений
Аналогично
Наконец, из равенств и
следует равенство отношений
следовательно,
что
влечет
![]()
Наконец, точка лежит на серединном перпендикуляре к отрезку
поскольку
Пусть
— середина
тогда
то есть
так же является серединой отрезка
следовательно, серединные
перпендикуляры к отрезкам
и
совпадают, значит
лежит на серединном перпендикуляре к
что завершает
доказательство.
Ошибка.
Попробуйте повторить позже
Диагонали и
трапеции
пересекаются в точке
а отношение оснований
Точки
и
— центры
окружностей
и
вписанных в треугольники
и
соответственно. Прямая, проходящая через точку
пересекает
в точках
и
а
— в точках
и
(
и
находятся ближе к
). Найдите радиус окружности
если
а
Источники:
Подсказка 1
Треугольники △AMD и △CMB подобны с коэффициентом 1/2, поэтому все соответствующие элементы относятся как 1/2. Нам дано произведение MZ*MY, которое напоминает произведение секущей на внешнюю часть. Но ведь мы знаем, что MZ/MX=1/2, поэтому легко находим MX*MY=10. А чему там равняется произведение секущей на внешнюю часть?
Подсказка 2
Конечно, квадрату отрезка касательной! Давайте отметим точку касания T: окружности ω₁ c отрезком BM. Тогда MT=√10. Если бы мы еще нашли MI₁, всё было бы в шоколаде...
Подсказка 3
Мы знаем, что MI₁/MI₂=2 и при этом MI₁+MI₂=13/2. Тогда MI₁=13/3. Воспользуйтесь теоремой Пифагора и завершите решение!
![]()
Пусть центр окружностей и
это
и
соответственно. Пусть точка
— точка касания
на
Тогда
| (1) |
Рассмотрим треугольники и
Они подобны с коэффициентом
Из этого следует, что
как
соответственные элементы в подобных треугольниках. Тогда
Используя , получаем
Пусть радиус это
тогда радиус
это
Тогда нужно найти
Рассмотрим
Из подобия и
получаем , что
из этого следует, что
Тогда
Ошибка.
Попробуйте повторить позже
Живописец закрасил акварелью полумесяц на клетчатой бумаге. Контур полумесяца состоит из двух дуг — одна от окружности с центром в
, проходящей через
, другая — от окружности с центром в
, проходящей через
. К утру краска расплылась так, что
каждая точка полумесяца превратилась в круг радиуса
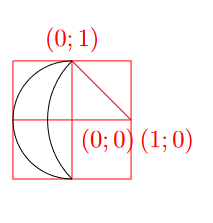
Найдите площадь получившейся фигуры.
Источники:
Подсказка 1
Когда краска расплылась, мы получили сложную фигуру, для площади которой точно не существует формулы. В таких случаях мы разбиваем фигуру на более простые, площади которых умеем вычислять.
Подсказка 2
Мы умеем находить площади окружностей, колец, секторов. Данная картинка удобно разбивается на эти фигуры или их части. При том, очевидно, что на концах нашего полумесяца нельзя брать целые окружности, потому что иначе усложняется вычисление площади остальной части фигуры. Подумайте, как можно, используя данные фигуры, разбить нашу?
Подсказка 3
Давайте разобьём фигуру на следующие части:
Пусть рисунок расплылся на радиус . К площади полумесяца прибавятся «поля», которые можно разбить на левое, правое и два
закругления на концах рогов.
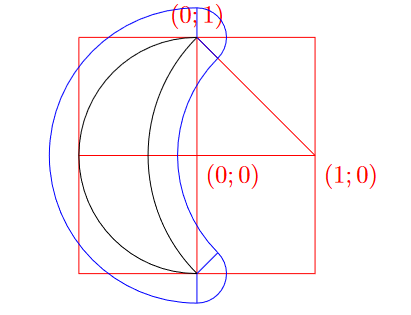
Площадь полумесяца равна половине площади круга радиуса минус сегмент круга радиуса
Площадь левого поля ”— половина от площади кольца с радиусами и
:
Площадь правого поля ”— четверть от площади кольца с радиусами и
:
Закругления на концах рогов вместе составляют три четверти окружности радиуса :
Вместе получается:
И тогда ответ:
Ошибка.
Попробуйте повторить позже
Две окружности радиусов и
касаются прямой
в точках
и
. Пусть
— точка пересечения этих окружностей,
наиболее удалённая от
. Докажите, что радиус описанной окружности треугольника
не зависит от положения
окружностей.
Не нарушая общности, точка принадлежит окружности радиуса
назовём её
а точка
принадлежит окружности радиуса
назовём её

Пусть
Тогда на дугу
в
опирается вписанный
угол
поэтому
аналогично
По теореме синусов имеем
что не зависит от положения окружностей.
Ошибка.
Попробуйте повторить позже
Окружности радиусов и
касаются внутренним образом в точке
. Хорда
большей окружности перпендикулярна
диаметру
меньшей окружности.
— одна из точек пересечения
с меньшей окружностью. Найти радиус окружности, описанной
около треугольника
.
Обозначим центры окружностей как и
соответственно.
Тогда .
![]()
Треугольники и
равнобедренные, пусть
и
Тогда по свойству внешнего угла треугольника
По теореме синусов в треугольнике получаем
По теореме синусов в треугольнике получаем
Теперь применим теорему синусов к треугольнику обозначив искомый радиус описанной около него окружности за
Следовательно
Ошибка.
Попробуйте повторить позже
В остроугольном треугольнике обозначили точку пересечения высот через
, центр описанной окружности через
. Площади
треугольников
и
равны 5 и 3 соответственно. Найдите площадь треугольника
.
Источники:
Подсказка 1
Итак, на нашем чертеже треугольник и две точки внутри него. Как-то пусто, и совсем не понятно, что с такой картинкой делать. Значит нужно придумать, что еще тут построить. Может быть, отметить какую-нибудь точку так, чтобы о прямой, соединяющей эту точку и центр описанной окружности нам было что-то известно. Что это может быть за точка?
Подсказка 2
Пусть М - середина стороны PV. Тогда ОМ перпендикулярна PV, а GM - медиана треугольника. Пусть GM пересекает отрезок ОН в точке Т. Вот, теперь чертеж выглядит поинтереснее! Рассмотрите его и найдите подобие.
Подсказка 3
Итак, треугольники GHT и OTM подобны. Но с каким коэффициентом? Чтобы это узнать, нужно заметить, что Н - это не абы что, а ортоцентр, и вспомнить его свойства.
Подсказка 4
По свойству ортоцентра GH = 2*OM. Получается, GT : TM = 2 : 1. Как тогда относятся друг к другу площади треугольников GHO и OHM?
Подсказка 5
Так же как 2 к 1! Теперь выразите площадь OHM через известные нам площади. Тут самое главное не забыть рассмотреть случаи!
В точке пересекаются три высоты треугольника. Так как
— центр описанной окружности, то в точке
пересекаются серединные
перпендикуляры треугольника. Пусть точка
— середина стороны
, тогда
медиана. Точка
— точка пересечения медианы и
прямой
.
![]()
Треугольники и
подобны (следует из параллельности прямых
и
, которые обе перпендикулярны
прямой
). Так как
(этот факт из школьной геометрии хорошо известен как "свойство ортоцентра"), то
коэффициент подобия равен 2. Значит,
, то есть медиана
делится точкой
в отношении
. Это
означает, что
- точка пересечения медиан треугольника
. Поэтому площадь
в 2 раза больше площади
.
Так как — середина
, то
Здесь ошибкой был бы вывод о том, что, значит, . Дело в том, что выше доказано, что одна из этих трех площадей
является суммой двух других. Но какая именно, зависит от рисунка, который мы сделаем. Важно, где прямая
пересекает стороны
треугольника. Если треугольник
правильный, то точки
и
совпадают и указанные в условии задачи три
площади вырождаются (это здесь невозможно, так как дано, что площади равны 3 и 5). Если прямая
проходит через
любую вершину треугольника, то тогда одна из трех площадей равна 0 , а две другие — ненулевые, но равны между собой
(тоже не наш случай). Если же прямая
пересекает две стороны (рассмотренный выше случай), то мы доказали, что
одна из этих трех площадей (в одном случае это
, в другом —
в третьем —
является суммой двух
других.
Поэтому получаем либо (то есть
), либо
(то есть
), либо
(что невозможно).
Ошибка.
Попробуйте повторить позже
В остроугольном треугольнике отметили основания высот
из вершин
и
соответственно. Пусть
—
окружности, вписанные в треугольники
и
соответственно, касающиеся сторон
и
в точках
и
соответственно. Пусть прямая
вторично пересекает окружности
в точках
и
соответственно. Докажите, что
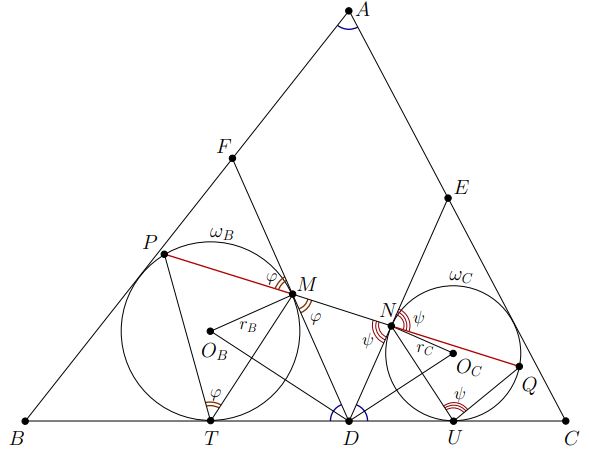
Пусть и
— центры
и
их радиусы —
и
а точки касания с
—
и
Из вписанных четырёхугольников
и
имеем:
Значит, прямоугольные треугольники и
подобны c коэффициентом
Пусть и
Прямые
и
касаются
и
откуда:
(Возможно, что точка или
совпала с
или
или лежит внутри треугольника
или
Чтобы убрать привязку к
конкретным случаям, можно использовать направленные углы)
В окружностях и
длины хорд
и
равны соответственно:
Напишем теорему синусов для треугольника
Наконец, собирая все полученные равенства:
получаем требуемое.
Ошибка.
Попробуйте повторить позже
Пусть — центр описанной окружности остроугольного треугольника
Прямая
пересекает высоты треугольника
из
точек
и
в точках
и
соответственно. Пусть
— ортоцентр треугольника
Докажите, что центр описанной окружности
треугольника
лежит на медиане треугольника
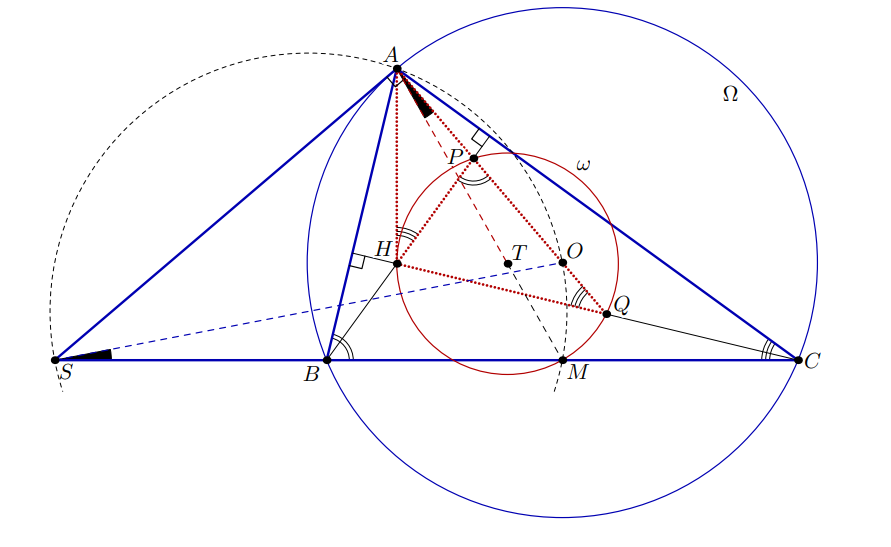
Пусть, не умаляя общности, Имеем
и аналогично
Следовательно, треугольники
и
подобны. Пусть
и
— описанные окружности треугольников
и
Поскольку
прямая
касается
Пусть — центр
и прямые
пересекаются в
Воспользуемся тем, что треугольники
и
подобны, и тем, что
касается
в
а точка
— лежит на
Рассмотрим касание
и
пусть
пересекает
в
Точки
и
соответствуют друг другу в подобных треугольниках
и
и следовательно
Следовательно
четырёхугольник
вписанный, и поскольку
имеем
Это значит, что
—
ортогональная проекция
на
которая является её серединой. Таким образом,
лежит на медиане
треугольника
Ошибка.
Попробуйте повторить позже
В треугольник со сторонами
,
вписана окружность с центром в точке
, которая касается сторон
и
в точках
и
соответственно. На прямой
отмечена точка
так, что угол
равен
. Найдите длину отрезка
.
Подсказка 1
Во-первых, давайте поймём, что у нас за картинка. А картинка у нас фиксирована, то есть мы можем вычислить (возможно, с большой сердечной болью) любой объект на картинке. А значит, скорее всего, задача на счёт. При этом, если мы уже хотим считать, то давайте посчитаем углы треугольника (возможно, угол OAK равен 60 градусам неспроста, иначе, непонятно как связать его хоть с чем-то)
Подсказка 2
По теореме косинусов угол ABC равен 60 градусам. Значит, угол AOC — 120. То есть, прямые OC и AK параллельны, а где параллельность — там и подобие.
Подсказка 4
Мы знаем KM, а значит, так как знаем KM и MT, то знаем и KN.
Заметим сразу, что , то есть треугольник
— остроугольный. А значит,
и
. Поэтому
точка
лежит снаружи треугольника
Обозначим углы треугольника за По теореме косинусов найдем угол
Проведем . Тогда
Поэтому, так как
по условию,
Пусть — точка пересечения
и
.
— биссектриса, медиана и высота в равнобедренном треугольнике
, поэтому
![]()
Тогда из прямоугольного треугольника получаем
По теореме косинусов найдем угол
По формуле половинного угла
По основному тригонометрическому тождеству
И тогда
А из треугольника находим
В итоге
Ошибка.
Попробуйте повторить позже
В
, биссектриса
Найти длины сторон
и
.
Источники:
Подсказка 1
Обозначим неизвестные стороны за переменные, пусть АВ = с, АС = b. Тогда по свойствам биссектрисы легко посчитать BL и LC.
Подсказка 2
Данный по условию cos∠A намекает нам на теорему косинусов. Но для каких треугольников её лучше записать?
Подсказка 3
Для △ABL и для △ACL! Все стороны для теоремы косинусов посчитаны. Вопрос только с углом. Но посчитать косинусы ∠BAL и∠CAL, зная, что cos∠A = 1/8, несложно!
Подсказка 4
Теперь осталось лишь решить эту не самую красивую систему из двух уравнений. Не забывайте, что b и c не просто переменные, а стороны △ABС, значит, для них должно выполняться неравенство треугольника.
Пусть . Если обозначить
через
, а
через
, то с помощью свойства биссектрисы нетрудно вычислить
.
![]()
Вычислим .
Теперь напишем теоремы косинусов для треугольников и
:
Вычтем одно равенство из другого и получим:
Если , то имеем
Тогда либо , либо
Первый вариант неверен, потому что тогда не будет выполняться неравенство треугольника . При втором варианте не
выполняется теорема косинусов для треугольника
Значит,
Решая это уравнение как квадратное относительно получаем
. Подставляя это в первое уравнение,
получаем
Этим значениям соответствуют
Ошибка.
Попробуйте повторить позже
На продолжении стороны квадрата
за вершину
отложен отрезок
Точка
— середина стороны
а
отрезки
и
пересекаются в точке
В каком отношении прямая
делит сторону
Подсказка 1
Хотим посчитать, в каком отношении PQ делит BC, давайте сперва обозначим их пересечение за X. Нас интересует BX/CX. Как можно посчитать такое отношение?
Подсказка 2
Верно, отношение можно посчитать по теореме Менелая для △ABC и прямой PQ. В ней будут помимо искомого участвовать выражения AP/PB и CQ/QA. Первое из них известно по условию, откуда брать второе?
Подсказка 3
Его можно найти из параллельности AB и MC, ведь образуются подобные треугольники ABQ и CMQ.
Обозначим пересечение с
за
![]()
Поскольку треугольники
и
подобны,
По теореме Менелая для
и прямой
Ошибка.
Попробуйте повторить позже
Прямая пересекает стороны
и диагональ
параллелограмма
в точках
и
соответственно. Докажите,
что
Подсказка 1
Чтобы доказать равенство, хочется все отношения получить на одной прямой. Например на AC, как бы отложить на AC первые два отношения?
Подсказка 2
Ага, из точек B и D можно провести прямые, параллельные l до пересечения с AC в точках E и F. Тогда перенеся отношения на прямую AC, остаётся доказать, что сумма AE и AF равна AC. Какой факт о точках E и F может в этом помочь?
Подсказка 3
Точки E и F симметричны относительно точки пересечения диагоналей параллелограмма, отсюда AE и FC (дополняющий AE до AC равны).
Проведём из точек и
прямые, параллельные
их пересечения с
обозначим за
и
соответственно. По теореме
Фалеса
Тогда требуется доказать, что Заметим, что точки
и
симметричны относительно точки пересечения диагоналей
параллелограмма, потому
из чего следует необходимое.
![]()
Ошибка.
Попробуйте повторить позже
Из вершины прямого угла прямоугольного треугольника
опущена высота
и в треугольнике
проведена биссектриса
Прямая, проходящая через точку
параллельно
пересекает прямую
в точке
Докажите, что прямая
делит
отрезок
пополам.
Подсказка 1
Обозначим пересечение AC и EF за X. Откуда будем считать отношение AX/XC?
Подсказка 2
Логично вычислять его из теоремы Менелая для △ACK и прямой EF. Задача сводится к равенству двух отношений, как же его доказывать?
Подсказка 3
Ага, можно воспользоваться свойством биссектрисы в △ACK, параллельностью CE и BF, а также образовавшимися при проведении высоты подобными треугольниками.
Запишем теорему Менелая для треугольника и прямой
пересечение
и
обозначим за
Тогда
Тогда необходимо доказать по свойству биссектрисы.
— высота в прямоугольном
следовательно
подобен
а значит,
Отметим, что
в таком случае по сумме углов треугольника и
оказываются равны, значит,
Итого осталось показать,
а это следует из параллельности прямых
и
![]()
Ошибка.
Попробуйте повторить позже
Пусть и
— параллелограммы, такие что
лежит на отрезке
а точка
на отрезке
Прямые
и
пересекаются в точке
Докажите, что точки
и
принадлежат одной прямой.
Подсказка 1
Требуется доказать факт лежания трёх точек на одной прямой, обычно это удобно делать по теореме Менелая, только вот на картинке нет подходящего треугольника - создадим его! Отметим точку X - пересечение FK и CD. Тогда как теперь записать требуемое?
Подсказка 2
Действительно, необходимо доказать, что выполняется теорема Менелая для △FDX и точек T, K, C. Возникающие в ней отношения FK/KX и XC/CD можно заменить на равные им AL/LD и FD/DA. Почему же полученное равенство выполняется?
Подсказка 3
Действительно, произведение трёх отношений равно 1, поскольку это условие теоремы Менелая для △AFD и точек B, T, L, лежащих на одной прямой.
Обозначим за пересечение
и
Наша цель — доказать, что выполняется условие теоремы Менелая для
и точек
Заметим, что из
из
Тогда доказать требуется, что
А это равенство верно по теореме Менелая для и точек
лежащих на прямых, содержащих его стороны и
принадлежащих одной прямой.
![]()
Ошибка.
Попробуйте повторить позже
Продолжения боковых сторон и
трапеции
пересекаются в точке
Произвольная прямая проходит через точку
пересечения диагоналей и пересекает основания
и
в точках
и
соответственно. Прямая
пересекает основание
в
точке
Докажите, что
Подсказка 1
В конструкции с параллельными прямыми и их секущими всегда возникают пары подобных треугольников. Какие пары треугольники в задаче являются подобными?
Подсказка 2
Например, подобны пары треугольников AFQ, CEQ и PEC, PKD. Чему равны отношения AF / EC и EC / KD (мы смотрим именно на эти отношения, поскольку в них фигурируют отрезки AF и KD равенство, которых нужно установить) из найденных подобий? Помните, что вы должны прийти к единообразию в полученных отношениях - будет проще, если каждое из отношений выразится через некоторые общие детали конструкции
Подсказка 3
Найденные отношения равны соответственно AF / EC = AQ / QC = AD / BC - это именно то, что мы хотели получить, отношения выразилось довольно просто только через элементы исходной трапеции. Выразите аналогичным образом отношение EC / KD и закончите решение
![]()
Поскольку
и
подобны, значит
Также подобны
и
из чего
Тогда
достаточно доказать, что
оба эти отношения равны
из подобий пар треугольников
и
и
Ошибка.
Попробуйте повторить позже
Точки и
расположены соответственно на сторонах
и
треугольника
причём
и
В каком
отношении отрезок
делит медиану
треугольника
Подсказка 1
Ясно, что надо как-нибудь привязаться к точке пересечения медианы и отрезка KN. Эту точку обозначим P. Отношения удобно искать через подобия. Можно ли на картинке найти подобные треугольники, хотя бы один из которых содержит P?
Подсказка 2
Можно! И даже оба треугольника будут содержать точку P: если провести KM — среднюю линию ABC, то у нас найдутся две параллельные прямые KM и AC. Какие тогда треугольники, содержащие P, подобны?
Подсказка 3
Конечно, это треугольники APN и MPK! А можно ли найти их коэффициент подобия?
Подсказка 4
Можно! Для этого снова используем, что KM - средняя линия, а потому 2KM = AC. Используя это свойство и данные из условия, можно легко получить ответ.
![]()
Обозначим точку — пересечение
и
Тогда
— средняя линия треугольника
значит
и
и
подобны. Значит



