Тема ПЛАНИМЕТРИЯ

Векторы и координаты в планиметрии

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела планиметрия

Разделы подтемы Векторы и координаты в планиметрии

Базовые операции с векторами на плоскости

Использование средней линии и середин отрезков через векторы

Длины векторов и скалярное произведение

Введение векторов или координат в планиметрии

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#76173

Дед Мороз наколдовал на серединах сторон треугольника $ABC$ шестиконечные снежинки, как показано на рисунке:

$PIC$

(вершина треугольника и середина стороны треугольника берутся концами стороны соответствующего правильного шестиугольника)

Докажите, что на полученном новогоднем чуде точки пересечения медиан треугольников $ABC$ и $XY Z$ совпадают.

Показать доказательство

Пусть $O$ — произвольная точка плоскости.

Про точку $M$ пересечения медиан треугольника $ABC$ известно, что:

−−→ −→ −−→ −−→ 3OM = OA +OB + OC

(это характеристическое свойство следует из того, что точка пересечения медиан является центром масс $−M−A→ +−M−B→ +−M−C→ = −→0$ )

А требуется доказать, что $M$ является ещё и точкой пересечения медиан треугольника $XY Z$ , то есть:

−−→ −−→ −−→ −→ 3OM = OX +OY + OZ

Левые части полученных двух векторных равенств совпадают, поэтому надо доказать про правые, что разность правых частей в этих равенствах равна нулевому вектору, то есть (преобразуем по правилу вычитания векторов):

−−A→X +−B→Z + −−C→Y = −→0

Возьмём серединный треугольник $A0B0C0$ и повернём его вокруг точки $M$ на $60∘$ . Получим треугольник $A1B1C1$ такой, что

A1B1 ∥ AX, B1C1 ∥BZ, C1A1 ∥CY

К тому же,

A1B1 =A0B0 = AB∕2= AX,B1C1 =B0C0 =BC ∕2= BZ,C1A1 = C0A0 = CA∕2 =CY

Значит,

−−→ −−−→ −→ −−−→ −−→ −−−→ AX = B1A1,BZ = B1C1,CY =C1A1

Но тогда получаем требуемое:

−−A→X +−B→Z + −−C→Y = −−B−1→A1+ −−B−1→C1+ −−C−1A→1 = −→0

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#79601

Векторы $⃗a ,⃗a,⃗a ,⃗a 1 2 3 4$ , расположенные в одной плоскости с вектором $⃗b$ , имеют равную длину, отличную от длины вектора $⃗b$ . Известно, что

−→ || || 9⃗a1− 4⃗a2− 5⃗b= 16⃗a3− 9⃗a4− 7⃗b= 0 ,|⃗a1− ⃗b|= 8

Найдите $|| ⃗|| |⃗a3− b|.$

Источники: ОММО - 2024, задача 4 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Давайте выразим всё через a₁ и a₃, ведь именно они выделяются: a₁ = 4/9 * a₂ + 5/9 * b, a₃ = 9/16 * a₄ + 7/16 * b. Что мы можем заметить здесь? А если вспомнить словосочетание «отношение отрезков»?

Подсказка 2

Это похоже на то, что мы взяли вектора a₂ и b, провели их от одной точки и на отрезке, который соединяет их концы, поставили точку с отношение 7/9, и вот этот вектор равен a₁. Аналогично с a_3. Как теперь можно наше наблюдение совместить с фактом про равные длины из условия?

Подсказка 3

Давайте создадим треугольник AOE, где OA = a₂, OE = b. Тогда вектор a₁ понятно находится по рассуждению выше. Но ведь у нас еще есть a₃. Пусть тогда OD = a₄. Тогда, опять же, a₃ понятно ищется на картинке. Но что же все таки с равными длинами? В какой конструкции у нас много точек на одном расстоянии лежит?

Подсказка 4

Верно! Концы векторов a₁, a₂, a₃, a₄ лежат на одной окружности, при этом прямые DC, AB, OE пересекаются в одной точке и делятся понятным отношением этой самой окружностью. Что тогда остается сказать, если даны окружность и отношения секущих?

Подсказка 5

Можно сказать, что у нас EB * EA = EC * ED, если BA = 4x, а EC = 9y, то y = x/2. Осталось воспользоваться условием задачи ещё раз

Показать ответ и решение

Выразим $⃗a = 4a⃗+ 5⃗b 1 92 9$ и $⃗a = 9-⃗a +-7⃗b 3 164 16$ . Поэтому $⃗a 1$ — чевиана в треугольнике $AOE$ со сторонами $OA = ⃗a 2$ и $OE =⃗b$ , которая делит третью сторону $AE$ в отношении $5$ к $4$ . А $a⃗3$ — чевиана треугольника $OED$ со сторонами $⃗ OE =b$ и $OD = ⃗a4$ , делящая $ED$ в отношении $9$ к $7$ . Так как векторы $⃗a1,⃗a2,⃗a3,⃗a4$ равны, то они лежат на окружности с центром в точке $O$ , а треугольники $AOB$ и $OCD$ — равнобедренные.

$PIC$

По теореме об отрезках секущих

4x ⋅9x= 9y⋅16y

Откуда

y = x 2

По условию $4x= 8$ , следовательно $|a⃗3− ⃗b|= 9y = 9.$

Ответ: 9

Ошибка.
Попробуйте повторить позже

Задача 3#82783

Старинный подземный ход имеет свод параболической формы (то есть в поперечном сечении туннель ограничен полом — осью $Ox$ и графиком некоторой параболы $2 y = a− bx$ ). Ширина туннеля (измеряется по полу) равна $24$ , высота туннеля равна $18$ . Ход укрепили распорками — на параболе отметили точки $A$ , $B$ , $C$ , $D$ и соединили их между собой балками. Балки $AB$ и $CD$ параллельны полу, $AD$ пересекается с $BC$ , и при этом $∘ ∠ACB = ∠ADB = 90$ . Найдите расстояние между балками $AB$ и $CD$ .

Источники: Ломоносов - 2024, 11.6 (см. olymp.msu.ru)

Подсказки к задаче

Подсказка 1

Давайте введем на нашей картинке систему координат, которая была бы нам удобна. К примеру симметричную относительно прямой симметрии параболы и нулевой высоты в тоннеле. Тогда, что нужно чтобы зафиксировать картинку? Каких параметров будет достаточно, чтобы выразить через это всю картинку?

Подсказка 2

Нам достаточно h - высоты вершины, а также длины основания - 2l(для симметрии). Тогда, если наша парабола задается функцией f(x) = a - bx^2, то f(l) = f(-l), f(0) = h. Тогда f(x) = h(1 - x^2/l^2). Значит, мы можем задать две точки A и C, а остальные - будут отличаться от симметричных только умножением на -1 абсциссы. Давайте так и сделаем - пусть x_1 - абсцисса А, а x_2 - абсцисса C. Тогда как нам выразить перпендикулярность, если мы работаем в координатах? Мы ведь не использовали еще ни разу тот факт, что, к примеру, AC и CB перпендикулярны.

Подсказка 3

Верно, мы можем выразить это через скалярное произведение векторов AC и CB. После того, как мы запишем и преобразуем выражение, у нас получится, что -(x_2^2 - x_1^2) - (h^2)/(l^4) * (x_2^2 - x_1^2)^2 = 0. Но при этом, у нас x_1 != x_2, поэтому x_2^2 - x_1^2 = - (h^2)/(l^4). Тогда, нам остается понять, чему равно расстояние между балками и записать ответ!

Показать ответ и решение

Обозначим ширину тоннеля за $2l$ , а высоту за $h$ . Из этих параметров однозначно выводятся параметры параболы: $x$ принадлежит отрезку $[−l,l],$ а $y(l)= y(−l)= 0,$ так что

hx2 y(x)= h− -l2-

Теперь зададим координаты точек так:

2 2 2 2 A = (x1,h(1− xl12 )),B = (−x1,h(1 − x1l2 )),C = (x2,h(1 − x2l2 )),D = (x2,h(1− x2l2 ))

Так как $AB$ и $CD$ параллельны полу, то понятно, что ординаты $A$ и $B$ одинаковы. Значит, абсциссы отличаются только знаком. Аналогично для $C$ и $D$ .

$PIC$

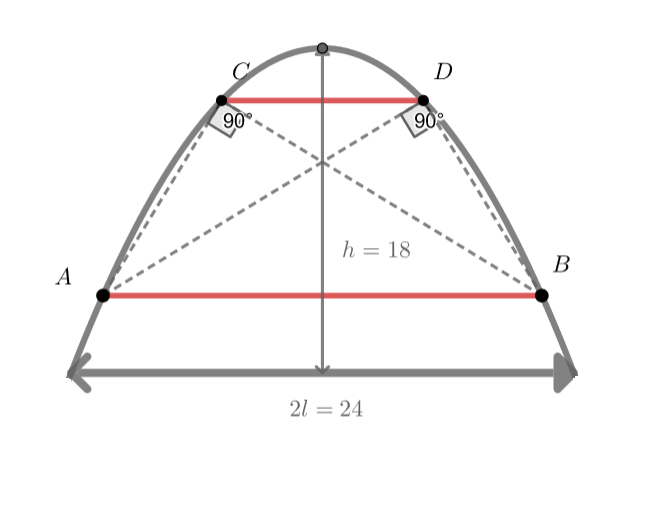
Тогда перпендикулярность $AC$ и $CB,$ $AD$ и $DB$ можно выразить, например, через равенство нулю скалярных произведений. Достаточно рассмотреть одну пару, так как рисунок симметричен.

AC = (x2− x1; h(x2− x2),CB = (−x1 − x2; h(x2− x2)) l2 1 2 l2 2 1

2 2 h2- 2 22 AC ⋅CB =− (x2− x1)− l4 (x2− x1)= 0

Тогда либо $2 2 (x2− x1) =0$ (но балки не совпадают, поэтому такой вариант не подойдет), либо

2 2 l4 (x2− x1)= − h2

А расстояние между балками это:

2 |hl2(x22− x21)|= lh-= 8

Ответ: 8

Ошибка.
Попробуйте повторить позже

Задача 4#85562

По плоскости ползут три улитки. Каждая улитка движется со своей скоростью прямолинейно и равномерно. Известно, что в некоторые три момента времени все улитки оказывались на одной прямой. Могут ли улитки в какой-то момент времени оказаться в вершинах правильного треугольника?

Источники: Курчатов - 2024, 11.4 (см. olimpiadakurchatov.ru)

Подсказки к задаче

Подсказка 1

Как в геометрии, так и в других разделах математики, зачастую бывает удобно зафиксировать задачу набором переменных. Если мы хотим зафиксировать задачу здесь, то самым банальным набором будет функция движения каждой улитки. Пусть (x_i(t), y_i(t)) - положение улитки относительно времени. Какое тогда условие, при наличии направляющих векторов можно наложить на их координаты, если в некоторый момент времени эти три улитки были

Подсказка 2

Верно, что (x_2(t) - x_1(t))(y_3(t) - y_1(t)) = (x_3(t) - x_1(t))(y_2(t) - y_1(t)). Просто записали векторное произведение векторов от первой ко второй улитке и от первой к третьей. Что теперь можно понять, если у нас нашлось 3 значения таких t(то есть, три раза был момент, когда они все на 1 прямой)? А если подумать какой степени каждая из зависимостей x_i, y_i относительно t?

Подсказка 3

Зависимости x_i, y_i - линейный зависимости(так как каждая улитка движется по линии), а значит, уравнение выше - не выше второй степени. Однако, у него есть три различных корня. Что это значит тогда? Когда такое может быть?

Показать ответ и решение

Введем декартову систему координат, и пусть $(x (t);y(t)),i= 1,2,3 i i$ - координаты $i$ -й улитки в момент времени $t$ . Поскольку улитки движутся прямолинейно и равномерно, то $xi(t)$ и $yi(t)$ - линейные функции от времени $t$ . Рассмотрим векторы

¯a(t)= (x (t)− x(t);y (t)− y (t)), 2 1 2 1 ¯b(t)=(x3(t)− x1(t);y3(t)− y1(t)),

направленные от первой улитки ко второй и третьей соответственно. Тогда условие принадлежности трех улиток одной прямой равносильно коллинеарности векторов $¯a(t)$ и $¯ b(t)$ .

Это в свою очередь равносильно пропорциональности координат этих векторов:

(x2(t)− x1(t))(y3(t)− y1(t))= (x3(t)− x1(t))(y2(t)− y1(t)).

Заметим, что это равенство представляет собой уравнение на переменную $t$ степени не выше 2. Нам известно, что у этого уравнения есть три различных корня. Но тогда это уравнение имеет тривиальный вид $0 =0$ , поскольку в противном случае у него не может быть больше двух корней. Значит, это уравнение справедливо при любом $t$ , и улитки всегда находятся на одной прямой и не могут оказаться в вершинах ни одного треугольника.

Ответ: нет

Ошибка.
Попробуйте повторить позже

Задача 5#87529

На каждой из двух прямолинейных линий электропередач установлены обслуживающие подстанции. На линии А — через каждые $m$ км, на линии В — через каждые $q$ км. Если занумеровать их подряд вдоль каждой линии, то расстояния между подстанциями $A1$ и $B1$ равно $√- 15 2$ км, между $A3$ и $B3$ равно $√-- 5 34$ км, между $A4$ и $B4$ равно $√-- 15 10$ км. Определите, параллельны ли данные линии? Если да, то найдите расстояние между ними. Если нет, то найдите расстояние от подстанции $A1$ до точки их пересечения.

Источники: Надежда энергетики - 2024, 11.2 (см. www.energy-hope.ru)

Подсказки к задаче

Подсказка 1

Как можно записать условие более ёмко? Можно ввести координаты.

Подсказка 2

Мы можем составить уравнение квадрата расстояния от Aₙ до Bₙ. Как оно может выглядеть?

Подсказка 3

Координаты подстанций будут линейно изменяться. Тогда расстояние можно представить как многочлен второй степени.

Подсказка 4

У нас есть 3 уравнения и 3 неизвестных, можем найти все коэффициенты многочлена. Как понять, будут ли линии пересекаться?

Подсказка 5

Значение многочлена всегда больше 0, так как дискриминант меньше 0. Тогда линии параллельны, а квадрат расстояния между ними равен минимальному значению многочлена. Его можно найти через вершину.

Показать ответ и решение

Если ввести декартову систему координат с началом в точке $A 1$ и одной из осей, направленной вдоль линии $A$ (можно и иначе), то координаты всех подстанций будут изменяться линейным образом, следовательно, квадраты расстояний $AkBk$ будут являться значениями некоторого многочлена второй степени $2 P(s)= as + bs+ c$ . Найдём его. Будем измерять $s$ в условных единицах длины, так что каждая следующая единица соответствует следующей паре подстанций. Тогда

2 P (0)= c= A1B1 = 9⋅50

2 P (2)= 4a+ 2b+ c= A3B3 = 17⋅50

2 P (3)= 9a+ 3b+ c= A4B4 = 45⋅50

Для простоты расчетов уменьшим все правые части в $50$ раз и из полученной линейной системы найдём

a= 8,b =− 12,c= 9.

Следовательно, искомый многочлен имеет вид

P(s)= 50(8s2− 12s+ 9)

Его дискриминант отрицателен, $P(s)$ нигде не обращается в ноль (и всюду положителен). Следовательно, линии не пересекаются. Квадрат расстояния между ними равен минимальному значению $P (s)$ , которое достигается при $s =s0 = 34$ и равно $50⋅ 92 = 225$ . А само расстояние равно 15.

Ответ:

Линии параллельны, расстояние между ними равно $15$ км.

Ошибка.
Попробуйте повторить позже

Задача 6#95899

Упростите выражение $AC-+ DE-+CB-+ EA.$

Подсказки к задаче

Подсказка 1

Мы работаем с векторами, поэтому хорошо бы вспомнить, а какие свойства есть у них? Если тяжеловато воспринимать просто выражение, то попробуйте нарисовать векторы на бумаге.

Подсказка 2

Верно, мы знаем, что AC+BC = AC (складываем как векторы). К тому же складывать мы можем в любом порядке. Попробуйте теперь, применив эти знания, упростить выражение!

Показать ответ и решение

Вспомним, что для любых точек $P,Q,R$ верно

--- --- --- PQ+ QS = PS,

а также, что сложение векторов коммутативно и ассоциативно, то есть

- - - - a+ b= b+a

(a+ b) +c= a+ (b+ c) .

Исходя из этих свойств:

AC+ DE-+ CB-+EA-= AC-+CB-+ DE-+ EA= AB-+ DA-=DA-+ AB-= DB-

Ответ:

$DB$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#95902

Упростите выражение $CE-− CA-+EB-− DB.$

Показать ответ и решение

--- --- --- --- CE− CA +EB − DB =

CE+ AC-+EB-+ BD-=

AC-+CE-+ EB-+ BD-=AD-

Ответ:

$AD$

Ошибка.
Попробуйте повторить позже

Задача 8#95903

(a) Пусть $AA1$ — медиана треугольника $ABC.$ Докажите, что

---- 1--- --- AA1 = 2(AB + AC)

(b) На стороне $BC$ треугольника $ABC$ выбрана точка $A1$ такая, что

BA1-= t. BC

Докажите, что

AA1 = (1− t)AB-+tAC

Показать доказательство

(a) Разложим вектор в сумму векторов

({ ---- --- ---- AA1-= AB-+BA1- ( AA1 = AC +CA1

Так как вектора $---- CA1$ и $---- BA1$ равны по модулю и противоположно направленны, то

---- ---- BA1 = −CA1,

тогда после сложения равенств системы

---- --- --- 2⋅AA1 = AB +AC

---- AB-+AC- AA1 = ---2---

(b) По условию $BA1 = t⋅BC,$ тогда

CA1 = BC − BA1 = (1− t)⋅BC

Следовательно,

( ---- --- ---- --- --- { AA1 =AB + BA1 =AB + t⋅BC ( AA1-=AC-+ CA1-=AC-− (1 − t)⋅BC

Домножим первое и второе равенство на $t− 1$ и $t$ соответственно. Тогда, сложив их, получим:

AA1 = (1− t)⋅AB-+t⋅AC

Ошибка.
Попробуйте повторить позже

Задача 9#95904

В четырёхугольнике $ABCD$ точка $M$ — середина $BC,$ $N$ — середина $AD.$ Докажите, что

BA+-CD-- MN ≤ 2

Когда достигается равенство?

Показать ответ и решение

Представим вектор $MN--$ в следующем виде:

({ MN--= MB-+ BA+ AN- ---- --- --- --- ( MN = MC + CD+ DN

Так как вектора $---- MB$ и $--- MC,$ $--- AN$ и $--- DN$ равны по модулю и противоположно направленны, то

---- --- --- 2⋅MN = CD +BA

---- CD-+BA- MN = ---2----

Тогда по неравенству треугольника получим, что

MN ≤ CD + BA-= BA-+CD-- 2 2 2

Равенство достигается, когда $CD-$ сонаправлен $BA,$ то есть, когда $CD ||BA.$

Ответ:

Когда $CD ||BA$

Ошибка.
Попробуйте повторить позже

Задача 10#97371

(a) Докажите, что сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.

(b) Докажите, что сумма квадратов сторон произвольного четырехугольника не меньше, чем сумма квадратов его диагоналей, причем равенство достигается только в случае параллелограмма.

Подсказки к задаче

Подсказка, пункт а

Введите векторы, образующие стороны параллелограмма. Честно напишите через эти 2 вектора сумму квадратов длин диагоналей и сумму квадратов длин всех четырех сторон.

Подсказка 1, пункт б

Введите векторы, образующие стороны четырехугольника, их получится 4. Как проверять то, что требуется в задаче? Нужно выразить все выражения через наши 4 вектора. Как понять, что равенство получается только в случае параллелограмма?

Подсказка 2, пункт б

Если перед вами параллелограмм, то противоположные векторы должны быть равны с обратным знаком, причем это равносильно. Подумайте, как это можно написать, и сведите задачу к этим двум выражениям.

Показать доказательство

(a) Пусть $v1,v2$ — векторы, образованные сторонами параллелограмма. Тогда диагонали параллелограмма образованы векторами $v1 +v2$ и $v1 − v2.$ Наконец, в силу билинейности скалярного произведения

2 2 (v1+v2) +(v1− v2) = (v1+ v2,v1+ v2)+ (v1− v2,v1− v2)=

2 2 =((v1,v1)+2(v1,v2)+(v2,v2)+((v1,v1)− 2(v1,v2)+ (v2,v2))= 2(v1 + v2)

(b) Пусть $v1,v2,v3,v4$ — векторы, образованные сторонами четырехугольника. Тогда векторы, образованные диагоналями четырехугольника, могут быть выражены как $v1+ v2,v2+ v3,v3+ v4,v4+v1.$ Тогда доказываемое неравенство можно представить в виде

(v + v − v − v )2 (v − v − v + v )2 v21 + v22 + v23 +v24 ≥-1--22-3---4 + -1---22-3---4

После раскрытия скобок в правой части, имеем

( ) ∑4 1 ∑4 i=1(vi,vi)≥ 4 2i=1(vi,vi)− 4(v1,v3)− 4(v2,v4)

4∑ (v,v)+ 2(v ,v )+ 2(v ,v )≥ 0 i=1 i i 1 3 2 4

(v1+ v3,v1+ v3)+ (v2 +v4,v2+ v4)≥0

(v1+ v3)2+ (v2 +v4)2 ≥0

последнее верно при любых $v1,v2,v3,v4,$ причем равенство достигается тогда и только тогда, когда $v1 = −v3,v2 =− v4,$ то есть когда исходный четырехугольник является параллелограмом.

Ошибка.
Попробуйте повторить позже

Задача 11#97373

Докажите, что для любых единичных векторов на плоскости $v , 1$ $v ,...,v 2 n$ можно выбрать знаки в выражении $± v ±v ± ...± v 1 2 n$ так, что длина получившегося вектора будет не меньше чем $√ - n.$

Подсказки к задаче

Подсказка 1

Будем для удобства считать, что выбраны векторы u_i с учетом знака. Запишите квадрат суммы векторов. Что после этого нужно доказать?

Подсказка 2

Преобразованиями получите, что нужно взять векторы u_i так, чтобы сумма попарных скалярных произведений была неотрицательна. Как это можно сделать? Вообще у нас в условии n векторов, поэтому можно попробовать провернуть индукцию.

Подсказка 3

Докажите базу для двух векторов. Как реализовать переход? Выделите слагаемые, в которые входит новый вектор. Как бы сделать там сумму поменьше?

Показать доказательство

Пусть вектор $u1$ равен вектору $v1$ с выбранным перед ним знаком. Тогда результирующий вектор имеет вид $∑n i=1ui.$ Тогда достаточно показать, что знаки можно выбрать таким образом, что

( ) ∑n ∑n ∑ 2 ∑k k∑ n≤ i=1 ui,i=1ui = ui + 2i⁄=j(ui,uj)= n+2 i⁄=j(ui,uj)

то есть таким образом, что

∑k 0 ≤i⁄=j(ui,uj) (∗)

Докажем возможность такого выбора индукцией по $n.$ База для $n =2$ очевидна: скалярные произведения $(v1,v2)$ и $(v1,−v2)$ противоположны по знаку, а значит, хотя бы одно из них неотрицательно. Пусть для некоторого $k$ существует комбинация знаков при которой верно неравенство $(∗).$ Заметим, что

k+∑1 ( ∑k ) k∑ ( ∑k ) (ui,uj)= uk+1, ui + (ui,uj)≥(∗) uk+1, ui i⁄=j i=1 i⁄=j i=1

Сумма $∑k i=1ui$ фиксирована и не зависит от знака $uk+1,$ следовательно, достаточно положить такой знак $uk+1,$ что произведение $( ∑k ) uk+1, ui i=1$ неотрицательно.

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#97374

Дан четырёхугольник $ABCD,$ в котором $AB = AD$ и $∠ABC = ∠ADC = 90∘.$ На сторонах $BC$ и $CD$ выбраны соответственно точки $F$ и $E$ так, что $DF ⊥ AE.$ Докажите, что $AF ⊥ BE.$

Подсказки к задаче

Подсказка

Самое сложно это грамотно ввести векторы. Как это сделать, чтобы их не было слишком много? Введите все векторы, которые чему-то перпендикулярны. Постарайтесь выразить через эти векторы условие и то, что требуется доказать.

Показать доказательство

Отрезки $AF$ и $DE$ перпендикулярны, следовательно, (здесь и далее в данной задаче, $XY ≡−X−Y→)$ получаем $(AE,DF )=0.$ Осталось заметить, что

(AE,DF )=(AE,DA + AF)= (AE,DA )+(AE,AF)=

2 2 = (AD + DE,DA )+(AE,AF )= −AD +(DE,DA )+(AE,AF )=− AB + (AE,AF)

= (AB +BF,BA )+(AE,AF )= (AF,BA )+(AE,AF )=(AF,BA +AE )= (AF,BE )

следовательно, отрезки $AF$ и $BE$ так же перпендикулярны.

$PIC$

Ошибка.
Попробуйте повторить позже

Задача 13#97377

Пусть $A A ...A 1 2 n$ — правильный $n$ -угольник, $X$ — произвольная точка. Рассмотрим проекции $X , 1$ $X ,...,X 2 n$ точки $X$ на прямые $A1A2,$ $A2A3,...,AnA1$ соответственно. Пусть $xi$ — длина отрезка $AiXi$ с учетом знака (знак плюс берётся в случае, когда лучи $AiXi$ и $AiAi+1$ сонаправлены). Докажите, что сумма $x1+ x2+...+xn$ равна половине периметра многоугольника $A1A2 ...An.$

Подсказки к задаче

Подсказка

Когда есть правильный многоугольник и вы хотите ввести векторы, очень полезно отметить его центр. Вам сразу легче становится выражать все векторы, а к тому же вы получаете прекрасное тождество - сумма векторов из O во все вершины равна 0. Сделайте это и в этой задаче, выразите все x_i через вектор OX, векторы выходящие из центра многоугольника и векторы сторон.

Показать доказательство

Достаточно рассмотреть случай, когда длины сторон многоугольника $A ...A 1 n$ равны $1.$ В этом случае $x = (A-X,−−A−−A−→) . i i i i+1$ Пусть $O$ — центр правильного многоугольника $A1...An.$ Тогда

∑n ∑n ( ) ( ∑n ) n∑ ( ) xi = −A−i→O,−−A−i−A−i+→1 + −−O→X, −−A−i−A−i+→1 = −A−i→O,−A−i−A−i−→+1 i=1 i=1 i=1 i=1

поскольку $∑n −−−−−→ −→ AiAi+1 = 0 i=1$ для любого многоугольника. Остаётся заметить, что

( −−→ −−−−−→ ) AiO,AiAi+1 = 1∕2

для всех $i.$

Ошибка.
Попробуйте повторить позже

Задача 14#97586

На плоскости нарисованы два квадрата $ABCD$ и $KLMN$ (их вершины перечислены против часовой стрелки). Докажите, что середины отрезков $AK$ , $BL$ , $CM$ и $DN$ являются вершинами квадрата.

Подсказки к задаче

Подсказка 1

Давайте подумаем, как можно доказать, что четырёхугольник является квадратом. Например, если доказать, что две соседние стороны равны и перпендикулярны, а потом сделать то же самое для других пар соседних сторон, то мы получим требуемое.

Подсказка 2

Реализовать задуманное можно через векторы. Если выразить векторы, соответствующие сторонам четырëхугольника, через векторы, про которые мы знаем побольше информации, а именно векторы сторон двух квадратов, то всё должно получиться.

Показать доказательство

Сформулируем и докажем следующюю лемму.

Лемма. Дан четырехугольник $ABCD$ , точки $M, N$ середины соотвественно сторон $AD$ и $BC$ , тогда

−→ −−→ −M−→N = AB-+-DC-. 2

Доказательство. Имеем

−−M→N = −−M→A + −A→B +−B−→N.

Аналогично

−M−N→ = −−M→D + −−D→C +−C−→N.

$PIC$

Поскольку $−M−A→ = −−M−→D$ и $−B−→N = −−C−→N$ , то, сложив полученные равенства и поделив на 2, получим требуемое.

_________________________________________________________________________________________________________________________________________________________________________________

Вернемся к доказательству исходной задачи. В силу леммы, имеем

−−→ −→ −−→ −→ −−→ −−→ PQ = AB-+-KL; QR = BC-+-LM- 2 2

Векторы $−→AB$ и $−K−→L$ получаются из векторов $−−B→C$ и $−L−M→$ поворотом на $90∘.$ Поэтому из приведенных выше равенств следует, что вектор $−Q→R$ получается из вектора $−−P→Q$ поворотом на $90∘,$ то есть отрезки $PQ$ и $QR$ равны и перпендикулярны. Аналогично, любые две стороны в четырехугольнике $P QRS$ равны и перпендикулярны.

$PIC$

Ошибка.
Попробуйте повторить позже

Задача 15#97590

Точка $K$ — середина стороны $AB$ квадрата $ABCD$ , а точка $M$ лежит на диагонали $AC$ , причём $AM :MC =3 :1.$ Докажите, что угол $KMD$ прямой.

Показать доказательство

Переведём задачу на язык векторов: $∠KMD$ прямой тогда и только тогда, когда скалярное произведение векторов $−M−K→$ и $−M−D→$ равно 0.

$PIC$

Выразим $−−→ MK$ через вектора $−→ AB$ и $−−→ AD$

−−→ −−→ −−→ 1−→ 3−→ 1−→ 3( −→ −−→ ) 1 −→ 3−−→ MK = AK − AM = 2AB − 4AC = 2AB − 4 AB+ BC = −4 AB − 4BC

Так как $ABCD$ — квадрат, то $−−→ −−→ AD = BC,$ тогда

−M−K→ = − 1−A→B − 3−B−→C =− 1−A→B − 3−A−→D 4 4 4 4

Выразим $−M−→D$ через вектора $−A→B$ и $−−A→D$

( ) −−M→D = −−A→D − −−A→M = −−A→D − 3 −A→C =−A−→D − 3 −A→B +−A−→D = 1 −−A→D − 3 −A→B 4 4 4 4

Теперь рассмотрим их скалярное произведение

−−→ −−→ ( 1−→ 3−−→ ) ( 1−−→ 3−→ ) -3−→ 2 3-−−→ 2 8-−→ −−→ MK ⋅MD = −4AB − 4AD ⋅ 4AD − 4AB = 16AB − 16AD + 16AB ⋅AD

Заметим, что раз $ABCD$ — квадрат, то $AB = AD$ и $∠BAD$ прямой, следовательно, $−→ 2 −−→2 AB = AD$ и $−→ −−→ AB ⋅AD = 0,$ тогда получаем

−−→ −−→ 3 3 MK ⋅MD = 16 − 16 = 0.

Значит, $∠KMD$ прямой.

Ошибка.
Попробуйте повторить позже

Задача 16#67114

В треугольнике $ABC$ точка $O$ — центр описанной окружности, точка $H$ — ортоцентр. Отрезки $OA,OB$ и $OC$ параллельно перенесли и последовательно приставили друг другу. Получилась ломаная. Докажите, что отрезок, соединяющий концы ломаной, равен и параллелен $OH.$

Подсказки к задаче

Подсказка 1

Отрезки, которые друг от друга откладывают, и нам важно только расстояние между началом и концом… Да это же задача на векторы! То есть нас просят доказать векторное равенство OH=OA+OB+OC (всё в векторах). Сразу такое доказывать страшно и не понятно как. Может быть преобразовать два каких-то слагаемых из этой суммы, с помощью дополнительного построения?

Подсказка 2

Если у нас есть ортоцентр, то надо пользоваться его свойством. При этом таким свойством, чтобы где-то обнаружить отрезок BH, потому что в данный момент совершенно неясно, что с ним делать, а только с ним что-то делать и остается, так как оба отрезка: OH и OB, как-то с ним связаны. Так какое доп. построение здесь может зарешать?

Подсказка 3

Оп-па, можно отразить точку О относительно AC (пусть образ точки O- это О₁). Тогда OO₁=HB, по свойству ортоцентра, при этом, очевидно, HBOO₁ — параллелограмм. А значит, OH можно легко выразить через OB и OO₁. Осталось выразить, в силу того, что СOAO₁ — параллелограмм, сумму векторов OA+OC, после чего увидеть, что задача решена!

Показать доказательство

Иными словами, нас просят доказать векторное равенство

−−→ −→ −−→ −−→ OH =OA + OB + OC(Формула-Гамильтона)

$PIC$

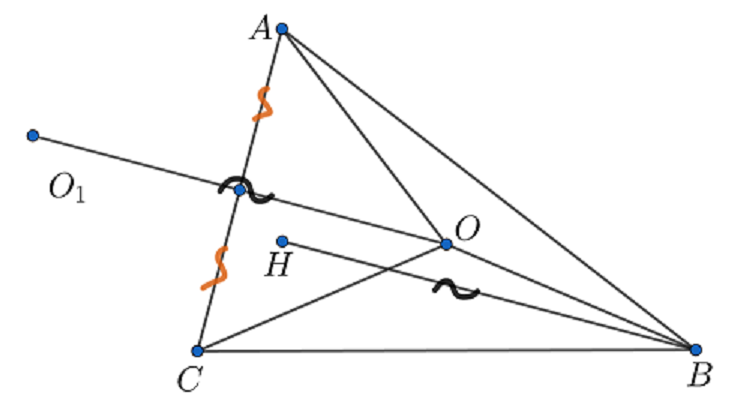
Пусть $O1$ симметрична $O$ относительно середины $AC,$ тогда

−O→A +−O−→C = −O−O→1.

По свойству ортоцентра $BH = OO1$ и $BH ∥ OO1,$ значит $HBOO1$ — параллелограмм, следовательно,

−−→ −−→ −−→ OB + OO1 = OH

Таким образом,

−→ −−→ −−→ −−→ OA + OB +OC = OH

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 17#68542

Пусть $ABCD$ и $AB C D 1 1 1$ — два параллелограмма с общей вершиной. Докажите, что один из векторов $BB- ,CC- 1 1$ и $DD- 1$ коллинеарен сумме двух других.

Подсказки к задаче

Подсказка 1

Как доказать, что сумма двух векторов коллинеарна третьему? Может, выразить каждый наш вектор через какие-то другие и доказать, что сумма двух равна третьему...

Подсказка 2

Попробуем для начала разобраться с BB₁. Видно, что BB₁=BA+AB₁. А что можно сказать про вектор DD₁?

Подсказка 3

DD₁=DA+AD₁. Видно, что вектора BB₁ и DD₁ не содержат в разложении одинаковых векторов. Может, тогда именно вектор CC₁ равен сумме BB₁ и DD₁?

Подсказка 4

Итак, CC₁=CB+BA+AB₁+B₁C₁=BB₁+CB+B₁C₁. Если мы докажем, что CB+B₁C=DD₁, то мы победили. А может, просто CB=DA и B₁C=AD₁? Вспомните, что ABCD и AB₁C₁D₁ - параллелограммы, и завершите решение!

Показать доказательство

$PIC$

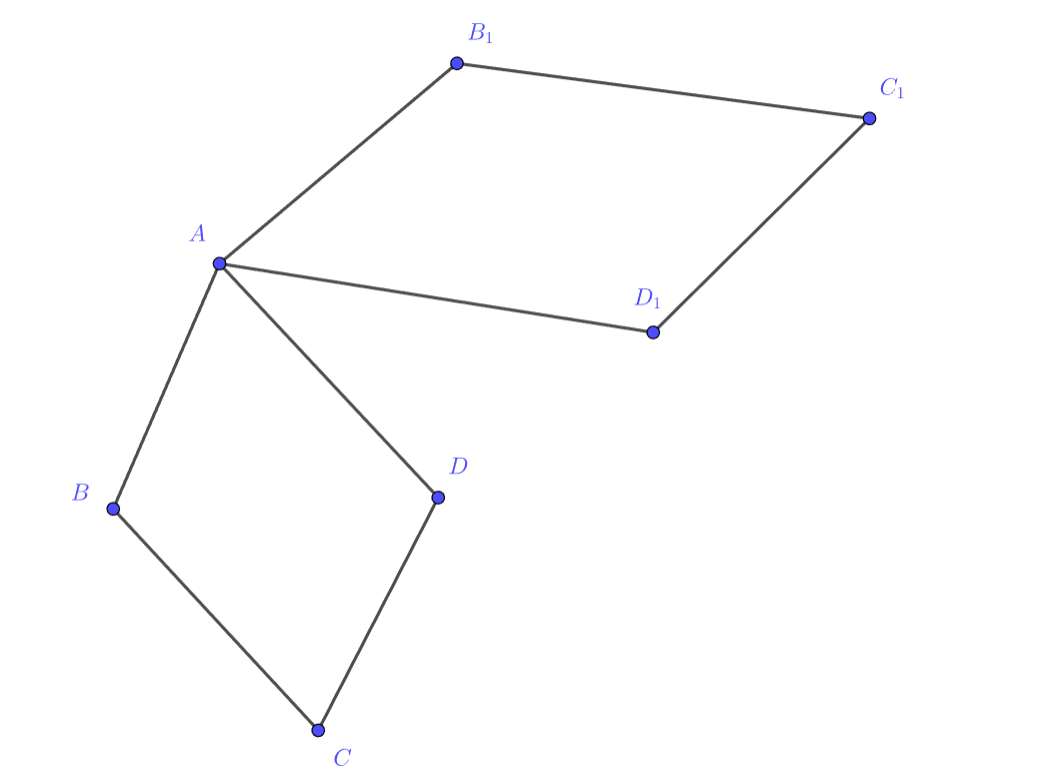
Выразим каждый из этих векторов через $−→ −−→ −−→ −−−→ AB,BC,AB1,B1C1$

−B−B→1 = −−A→B + −−A→B1, −D−D−→1 = −−D→A +−A−D→1 = −−B−→C + −−B−1→C1

Наконец,

−−→ −−→ −→ −−→ −−−→ −−−→ −−→ CC1 = −BC − AB +AB1 +B1C1 = DD1+ BB1

Ошибка.
Попробуйте повторить позже

Задача 18#68554

Из медиан треугольника $ABC$ составлен треугольник $A B C , 1 1 1$ а из медиан треугольника $A B C 1 1 1$ составлен треугольник $A B C . 2 2 2$ Докажите, что треугольники $ABC$ и $A2B2C2$ подобны, и найдите коэффициент подобия.

Подсказки к задаче

Подсказка 1

Для начала надо построить треугольник A₁B₁C₁. Вы же помните, как выражается вектор медианы через вектора сторон?

Подсказка 2

Если проведена медиана AM₁, то вектор AM₁ равен полусумме векторов AB и AС. Нетрудно увидеть, что сумма векторов AM₁, BN₁ и CK₁ равна 0 (BN₁ и CK₁- векторы оставшихся медиан), а значит из них действительно можно сложить треугольник. Может тогда посмотрим, как выражаются медианы треугольника A₁B₁C₁?

Подсказка 3

Мы знаем, что для векторов нашего треугольника A₁B₁C₁ верны следующие равенства: A₁B₁= AM₁, B₁C₁=BN₁, C₁A₁=CK₁. Тогда вектор медианы A₁M₂ равен полусумме векторов AM₁ и K₁C. Как тогда можно выразить вектор A₁M₂ через вектора треугольника ABC?

Подсказка 4

A₁M₂=(AM₁+M₁C)/2=(AB+AC+BC+AC)/4=3*AC/4. Осталось аналогично выразить остальные векторы медиан B₁N₂ и C₁K₂ и завершить решение!

Показать ответ и решение

Первое решение.

Пусть медианы $△ABC$ будут $′ AA ,...$ и аналогично для $△A1B1C1$ ( $′′ A1A ,...$ ). Тогда из $△ABC$ имеем

−→ −→ −→ −−→ −−→ −→ −A−→A ′ =AB-+-AC , −B−B→′ = BA+-BC-, −C−C→′ = CB+-CA 2 2 2

Заметим, что сумма всех векторов равна нулю, поэтому из них можно составить треугольник. Это важно, поскольку тогда мы можем использовать их в качестве сторон $A1B1C1$ ( $−A−→A′ → −A−1−B→1,−B−B→′ → −B−−1→C1,−C−C→′ → −C−1−→A1$ ). Далее из треугольника $△A1B1C1$ получим

−−−→ −−−→ −−−→ −→ −→ −−→ −→ −→ A1A′′= A1B1-+A1C1 = AB-+AC-+-BC-+AC- = 3AC-- 2 4 4

Здесь мы воспользовались тем, что $−A→B + −−B→C +−C→A = −→0 .$ Повторяя аналогичные рассуждения для остальных сторон, получаем подобие с коэффициентом $34.$

Второе решение.

Если стороны треугольника равны $a,b,c,$ то квадраты длин медиан выражаются по формулам

m2 = 2b2+-2c2-− a2 a 4

2 2c2+-2a2− b2 mb = 4

2 2a2+ 2b2− c2 mc = ----4------

Тогда у треугольника $A2B2C2$ квадраты длин сторон, как медианы треугольника $A1B1C1,$ выражаются по формулам

2 2 2 2m-b +2m-c − m-a= 4

= -1⋅(2(2b2+ 2c2− a2)+2(2c2+ 2a2− b2)− (2a2+ 2b2− c2)) 16

-1 ( 2) ( 3c)2 = 16 ⋅9c = 4

Далее аналогично считаются длины оставшихся двух сторон. В итоге у треугольника $A2B2C2$ стороны равны $34c,34b,34a,$ поэтому он подобен исходному треугольнику со сторонами $a,b,c,$ коэффициент подобия равен $3. 4$

Ответ:

$3 4$

Ошибка.
Попробуйте повторить позже

Задача 19#69112

В треугольнике $ABC$ на стороне $AB$ выбраны точки $K$ и $L$ так, что $AK = BL,$ а на стороне $BC$ — точки $M$ и $N$ так, что $CN = BM.$ Докажите, что $KN + LM ≥ AC.$

Подсказки к задаче

Подсказка 1

Давайте обратим внимание на схожесть расположения каждого из отрезков нашего неравенства. Каждый из них включен в треугольник с вершиной B. Попробуйте выразить вектора AC, KN и LM через вектора выходящие из вершины B.

Подсказка 2

Не просто же так в условии сказано, что BL=KA, а BM=NC. Подумайте, почему эти же равенства будут верны и в векторном виде и подставьте их в выражения, которые мы находили ранее. Подумайте, как теперь мы можем связать вектора AC, KN и LM.

Подсказка 3

Если до этого вы всё сделали правильно, то должны были получится векторные равенства: KN = BN - BK, LM = NC - KA. Если сложить два векторных равенства, то получим KN+LM=(BN+NC)-(BK+KA)=BC-BA=AC. Подумайте, почему данное векторное равенство доказывает неравенство из условия.

Показать доказательство

Рассмотрим для определенности конфигурацию, изображенную на рисунке

$PIC$

Тогда имеем следующие равенства:

( ||| −A→C =−B−→C − −B→A { −−K→N = −−B→N − −−B→K |||( −−→ −−→ −→ LM = BM − BL

Поскольку $−−→ −−→ BM = NC,$ а $−→ −−→ BL = KA,$ то сложив второе и третье равенства получим

−−→ −−→ (−−→ −−→ ) (−−→ −→ ) −−→ −→ −→ KN + LM = BN + BM − BK + BL =BC − BA = AC

Следовательно

|−A→C |= |−−L→M +−K−N→|≤ |−L−→M |+ |−K−→N |

Заметим, что при таком решении не существенно, как расположены точки $K, L, M$ и $N.$

Ошибка.
Попробуйте повторить позже

Задача 20#69114

Дан четырёхугольник $ABCD.A ′,B′,C′$ и $D′$ — середины сторон $BC, CD,DA$ и $AB$ соответственно. Известно, что $AA′ = CC′$ и $′ ′ BB = DD .$ Докажите, что $ABCD$ — параллелограмм.

Подсказки к задаче

Подсказка 1

Нам сказали про середины сторон, которые намекают нам на медиану...а что мы умеем делать с медианой в векторах?

Подсказка 2

Выражать ее через стороны треугольника! Т.е. каждый отрезок вида X'X мы можем выразить и записать систему равенств...что из нее видно?

Подсказка 3

Сумма векторов A'A + B'B + C'C + D'D = 0. Что это значит?

Подсказка 4

Из них можно составить четырехугольник с помощью параллельных переносов! Осталось лишь использовать равенства из условия и прийти к параллелограмму)

Показать доказательство

$PIC$

Так как точки $A′,B′,C′$ и $D ′$ являются серединами соответствующих сторон, то

( |||| −A−A→′ = −−→AB+2−−A→C |||{ −−→′ −−B→D+−B−→C- | B−B−→ = −−→2−−→ ||||| CC ′ = C−−D→+2C−A−→ |( −D−D→′ = DB+2DA

Складывая, получим, что

−A−A→′+−B−B→′+−C−C→′+−D−D→′ = −→0

Значит, данные отрезки можно параллельно перенести так, чтобы образовался четырёхугольник. Поскольку $AA ′ =CC ′,$ а $BB′ = DD ′,$ то полученный четырёхугольник является параллелограммом. Следовательно, прямые $AA′$ и $CC′$ параллельны и четырёхугольник $AA ′CC ′$ — параллелограмм, откуда следует, что отрезки $AC′$ и $CA′$ параллельны и равны. Но тогда стороны $BC$ и $AD$ параллельны и равны, то есть $ABCD$ — параллелограмм.

Предыдущий раздел

Следующий раздел