Подобные треугольники и теорема Фалеса
Ошибка.
Попробуйте повторить позже
Окружность с диаметром
пересекает сторону
остроугольного треугольника
в точке
Точка
выбрана на отрезке
так, что
а
— точка пересечения отрезка
с окружностью
, отличная от
. Найдите
если
Источники:
Подсказка 1
Вспомните свойства окружности и попробуйте повыражать углы.
Подсказка 2
Заметьте, что ∠ABE = ∠ADE. Как можно выразить ∠ADF?
Подсказка 3
∠ADF = 90° - ∠DAF = ∠ACD.
Подсказка 4
Попробуйте найти подобные треугольники.
Подсказка 5
△ABE ∼ △ADF ∼ △ACD. Выразите стороны при помощи косинуса.
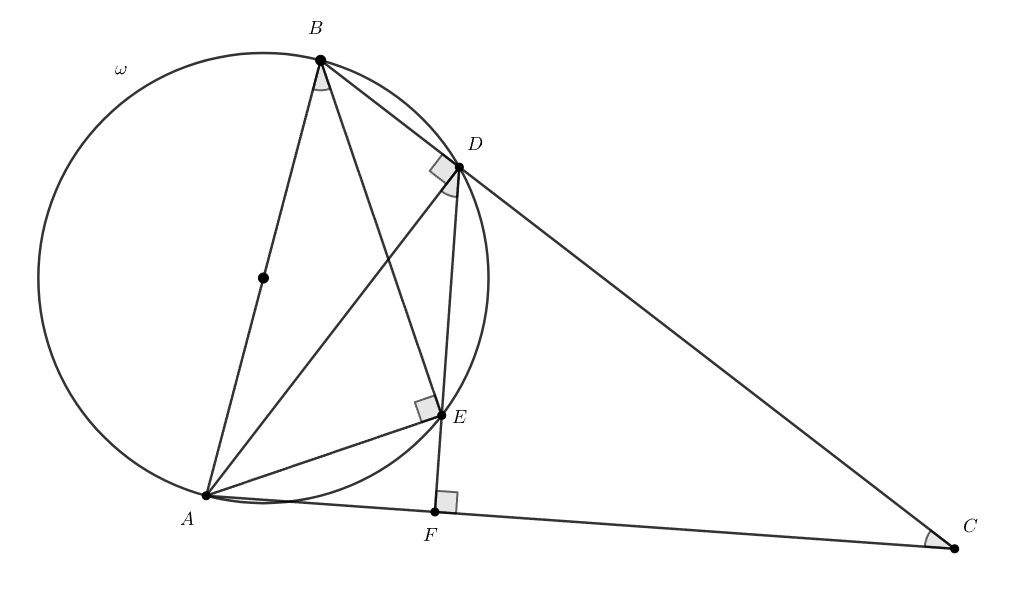
Заметим, что как вписанные углы, опирающиеся на дугу
Кроме того,
Значит,
Но тогда треугольники
— прямоугольные и имеют равные острые углы, следовательно, они подобны. Из
треугольника
получаем, что
Из треугольника
Из треугольника
Значит,
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




