Подобные треугольники и теорема Фалеса

Пусть — основание высоты из точки а — основание перпендикуляра, опущенного из точки на Прямая — серединный перпендикуляр к отрезку поэтому она параллельна высоте

По свойству ортоцентра и По условию прямые и параллельны, следовательно, — прямоугольник и

Первое решение.

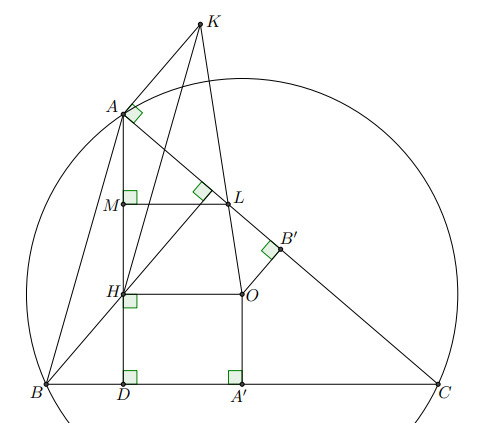
В параллелограмме противоположные стороны равны, поэтому Треугольники и подобны по двум углам ( как вертикальные, и их коэффициент подобия равен 2. Пусть тогда и поскольку — середина стороны Стало быть, и так как треугольники и подобны. Пусть тогда и Следовательно, и Таким образом,

______________________________________________________________________________________________________________________________________________________

Второе решение.

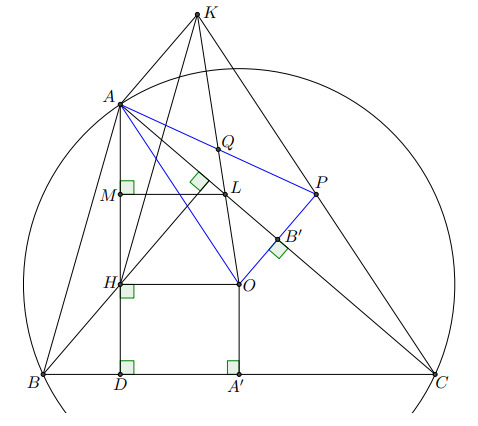
По условию прямые и параллельны, а прямая перпендикулярна прямой поэтому По условию параллелограмм, значит, Отрезок — средняя линия треугольника поэтому Кроме того, и перпендикулярны поэтому точки и лежат на одной прямой. Таким образом, и параллельна Стало быть, — параллелограмм. Пусть — точка пересечения его диагоналей, тогда Следовательно, и — медианы треугольника , а — точка их пересечения, поэтому и, значит, Из подобия треугольников и следует, что Тогда если то и а, значит, и

______________________________________________________________________________________________________________________________________________________

Третье решение.

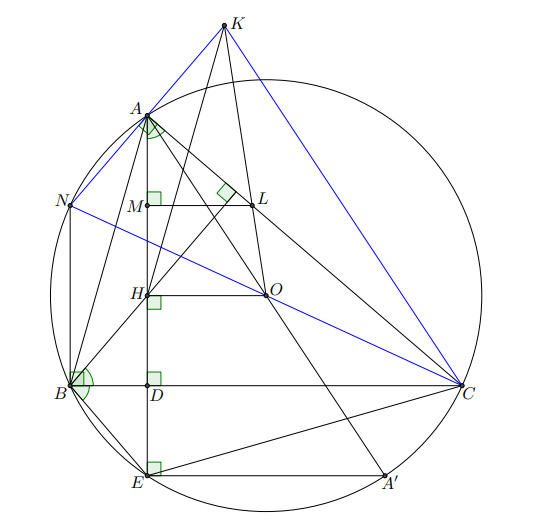
Пусть точка — пересечение этой высоты с описанной окружностью треугольника точка диаметрально противоположна точке на этой окружности, а точка — вторая точка пересечения прямой с этой окружностью. Из параллельности прямых и следует, что прямая перпендикулярна высоте Поскольку — диаметр окружности, и, значит, прямые и параллельны. Стало быть, — средняя линия треугольника поэтому Далее,

поэтому в треугольнике отрезок является биссектрисой и высотой, а, значит, и медианой. Таким образом, Из равенств и получаем, что

По условию прямые и параллельны, а прямая перпендикулярна прямой поэтому и точки и диаметрально противоположны. Следовательно, и поэтому прямые и параллельны. Таким образом, четырехугольник является параллелограммом. Стало быть, и отрезок является медианой в треугольнике Но отрезок также является медианой в этом треугольнике. Следовательно, — точка пересечения медиан этого треугольника и Тогда по теореме Фалеса Но мы уже знаем, что поэтому