Теоремы Менелая и Чевы, Ван-Обеля и Жергонна
Ошибка.
Попробуйте повторить позже
В треугольнике стороны
paвны
и
соответственно. Пусть точка
лежит на продолжении стороны
за точку
так, что
Пусть точка
лежит на стороне
так, что
Пусть
и
пересекаются в точке
Найти площадь
Подсказка 1
У нас есть треугольник ABC и три точки, лежащие на его сторонах, причём все три лежат на одной прямой. Какой сюжет напоминает? ;)
Подсказка 2
Воспользуемся теоремой Менелая для треугольника ABC! Какие отрезки мы можем найти с помощью неё? Также подумаем, через какие объекты можно найти площадь нужного нам четырёхугольника?
Подсказка 3
Площадь нужного нам четырёхугольника есть разность площадей двух треугольников! А что общего есть у этих треугольников?)
Подсказка 4
Треугольники ABC и ADE имеют общий угол, поэтому удобно считать их площадь через синус! Но где же взять значение этого синуса....?
Подсказка 5
Чтобы найти синус угла A, воспользуемся теоремой косинусов для треугольника ABC, ведь не зря нам дали все его стороны ;)
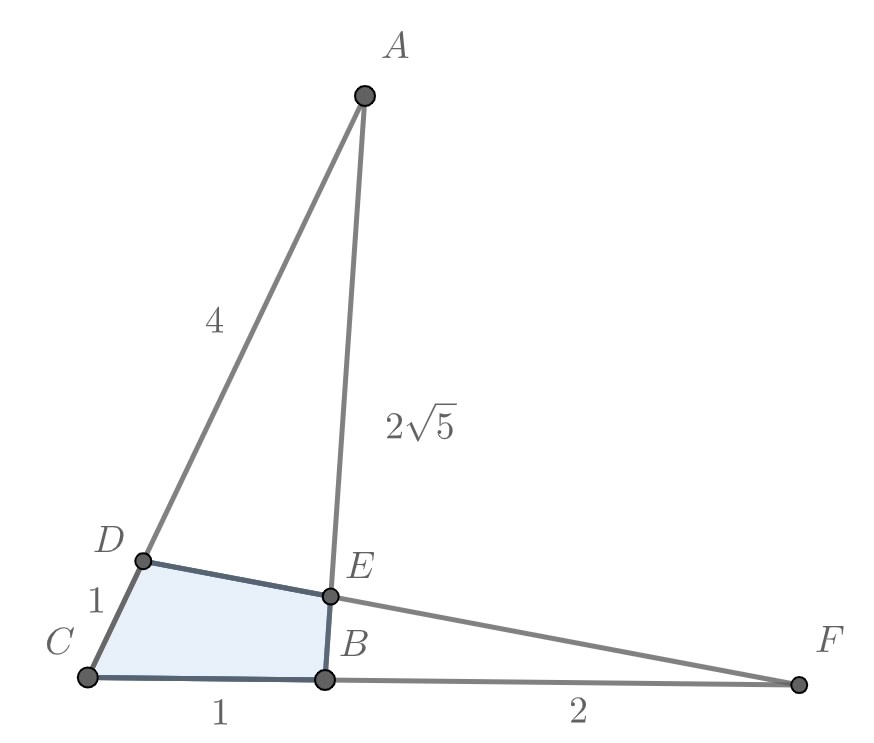
Из условия сразу получаем, что Также запишем теорему Менелая для
и прямой
Откуда получаем, что Запишем теорему косинусов для
Так как угол в треугольнике менее то
будет положительный, а именно:
Выразим площадь четырехугольника
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




