Теоремы Менелая и Чевы, Ван-Обеля и Жергонна
Ошибка.
Попробуйте повторить позже
В треугольнике проведена высота
На ней отмечена точка
Через точку
проведены отрезки
к
сторонам треугольника, а
пересекает
в точке
Известно, что
Найти длину
Источники:
Подсказка 1
У нас есть три чевианы, пересекающиеся в одной точке. На какую теорему это может нам намекать?
Подсказка 2
Верно, на теорему Чевы! Распишите её для △ABC. Но что делать с этим выражением? У нас есть произведение отношений, которыми чевианы делят стороны треугольника. Но что ещё чевианы делят в таком же отношении?
Подсказка 3
Да, площадь треугольника! Замените некоторые отношения сторон на отношения площадей, а затем распишите площади по теореме синусов. Какой отсюда можно сделать вывод об ∠KHF и ∠FHT?
Подсказка 4
Правильно, они равны! Тогда что интересного можно сказать про прямую HC?
Подсказка 5
Она является внешней биссектрисой △HKT! Осталось применить основное свойство биссектрисы:)
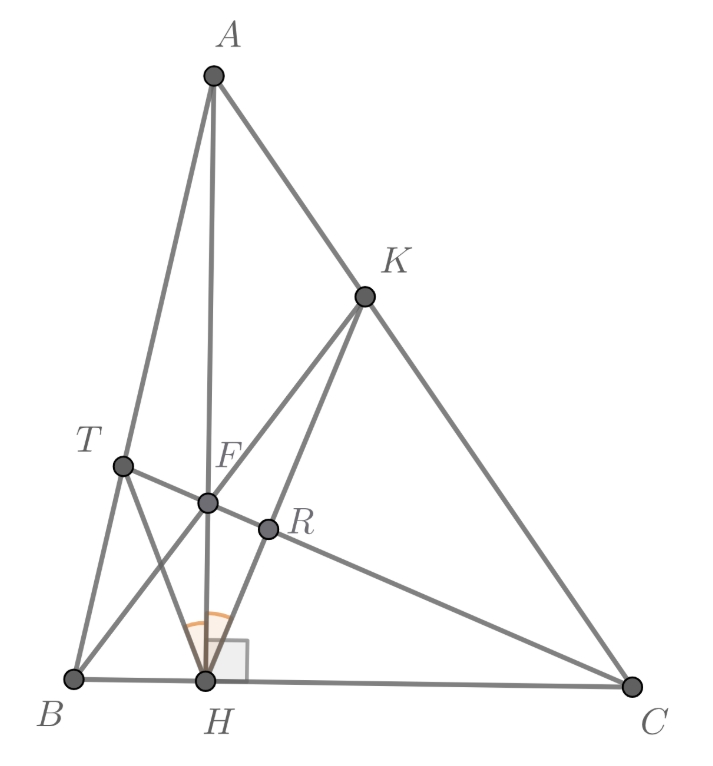
Докажем сначала, что — биссектриса
Это доказывается с помощью теоремы Чевы для
Так как чевиана делит площадь треугольника и его сторону в одинаковом отношении, то
Подставим эти отношения в равенство из теоремы Чевы и распишем площади:
Далее, так как — внешняя биссектриса
то
Далее замечаем, что Тогда
Значит,
Следовательно,
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




