Лемма 255
Ошибка.
Попробуйте повторить позже
В треугольнике точки
— середины сторон
а
,
— точки касания этих сторон со вписанной
окружностью соответственно. Прямые
пересекают
в точках
и
Докажите, что прямая
делит отрезок
пополам.
Источники:
Подсказка 1
Один отрезок делит другой пополам, часто это происходит потому что они являются диагоналями некоторого параллелограмма.
Подсказка 2
В данном случае окажется, CXC1Y - параллелограмм, но нужно как-то подобраться к точкам X и Y...
Подсказка 3
В этом нам поможет лемма 255, согласно ней точки X и Y лежат на биссектрисах углов A и B соответственно.
Докажем, что точки лежат на биссектрисах углов
соответственно (это утверждение известно как задача
и может быть
использовано на олимпиаде без доказательства). Так как
и
то
следовательно,
и
Аналогично
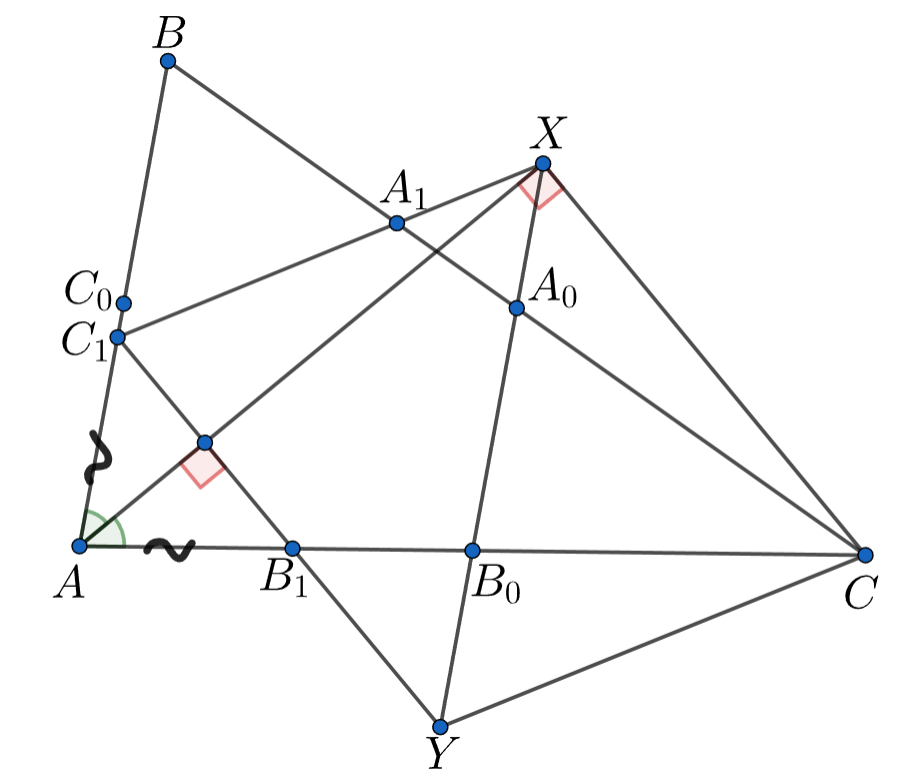
Итак, по лемме
и
потому что треугольник
равнобедренный и
в нём биссектриса,
проведённая к основанию. Следовательно,
Аналогично
Таким образом, четырёхугольник
—
параллелограмм. В таком случае его диагонали точкой пересечения делятся пополам, это даёт нам требуемое.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




