.03 Движение с переменным ускорением
Ошибка.
Попробуйте повторить позже
В безветренную погоду на озере была проведена серия испытаний радиоуправляемой модели катера с бензиновым
двигателем, в ходе которых выяснилось, что при скорости путевой расход топлива составляет
, а при скорости
расход равен
. Запас топлива на борту модели
.
Выведите зависимость путевого расхода топлива
от скорости
.
Какое максимальное время
может работать двигатель у неподвижной модели?
При какой скорости модели
путевой расход топлива минимален и каково его значение
? Полученные результаты
должны быть найдены с погрешностью, не превышающей
.
На какое максимальное расстояние
и за какое время
сможет уплыть модель?
Какое значение
может принимать время прохождения моделью расстояния
?
Примечание. Считайте, что при работе двигателя массовый расход топлива линейно зависит от мощности силы
сопротивления, а сила сопротивления пропорциональна скорости модели относительно воды. Модель движется
равномерно, и при любой скорости её осадка не меняется.
(Всеросс., 2017, финал, 9)
Источники:
При движении со скоростью расстояние
катер преодолевает за время
При этом мощность сил
сопротивления равна
где – размерный коэффициент.
Так как по условию массовый расход топлива линейно зависит от мощности сил сопротивления
где и
– размерные коэффициенты, то линейный расход топлива равен
Найдем константы и
по известным значениям
,
,
и
. Для этого запишем уравнения для линейного
расхода
Решая систему, получим:
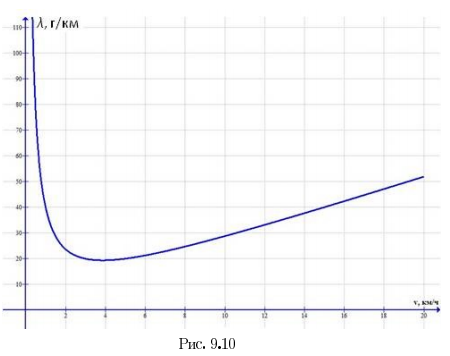
С учетом найденных размерных коэффициентов уравнение для линейного расхода приобретает вид:
График этой зависимости представлен на рисунке 9.10.
В режиме холостого хода двигатель неподвижный модели сможет проработать мин. Умножим
полученное выражение для
на
, получим квадратное уравнение (с размерными коэффициентами, полученными
ранее)
дискриминант которого обращается в ноль при , что соответствует
.
Максимальное расстояние, на которое может уплыть модель, двигаясь с оптимальной скоростью, , и
на его преодоление требуется время
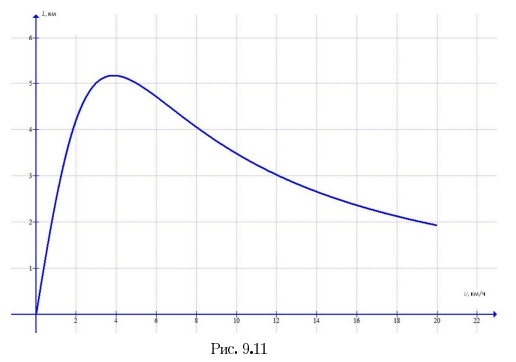
. Зависимость предельной дальности движения от скорости
приведена на рисунке 9.11.
Так как требуемое расстояние меньше предельной дальности
, то модель не обязана придерживаться
оптимальной стратегии и может плыть быстрее или медленнее. Из ранее полученного квадратного уравнения
с учетом
. Выбирая при решении больший корень, находим
максимально допустимую скорость
, при которой ещё хватает топлива на заданной дистанции
, и получаем соответствующее ей минимально возможное время движения
. Большему корню
соответствует максимально возможное время движения
. Окончательно получаем
(Официальное решение ВсОШ)
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




