.21 Центр масс
Ошибка.
Попробуйте повторить позже
Найдите положение центра масс системы касающихся друг друга шаров (рис.). Все шары имеют одинаковый диаметр
а их массы возрастают по закону:
где
Плотность
каждого шара постоянна.
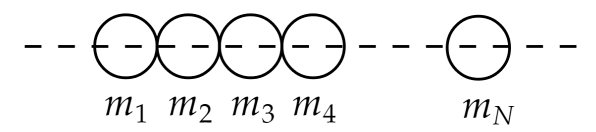
(Всеросс., 1997, ОЭ, 10)
Источники:
1. Введем координатную ось так, как показано на рисунке:
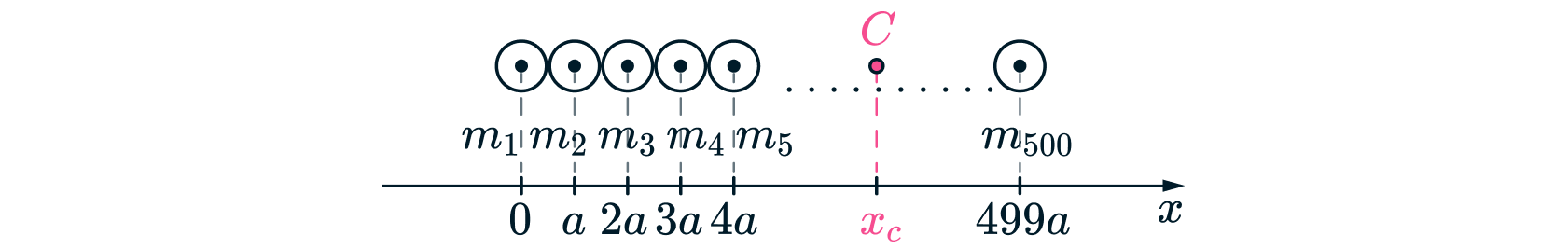
Воспользуемся формулой для координаты центра масс системы:
Перепишем в виде ряда:
Воспользуемся свойством и получим (для компактности записи не будем писать индексы
суммирования):
2. Посчитать слагаемые и
не составляет труда. В первом случае это сумма арифметической прогрессии, во
втором — просто единица взятая
раз. А как быть с суммированием квадратов?
Заметим следующее: при суммировании ых степеней мы получаем в итоге многочлен
ой степени
относительно
— это не сложно проверить как-минимум для
-ых и
-ых степеней.
Вот к примеру воспользуемся формулой суммы арифметической прогрессии и просуммируем 1-ые степени от до
:
Действительно получили многочлен 2-ой степени по .
3. Тогда для ожидается многочлен 3-ей степени по
:
Чтобы найти коэффициенты, посчитаем руками сумму для
, получим систему уравнений
относительно
и решим её:

Из каждого уравнения вычтем первое уравнение системы и сведем ее к системе из трех уравнений (избавимся от
):
Подставляем полученные коэффициенты в первое уравнение предыдущей системы и получим .
Получили формулу:
4. Вычислим все суммы в нашей формуле для координаты центра масс:
Тогда
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




