.03 Закон сохранения и изменения импульса
Ошибка.
Попробуйте повторить позже
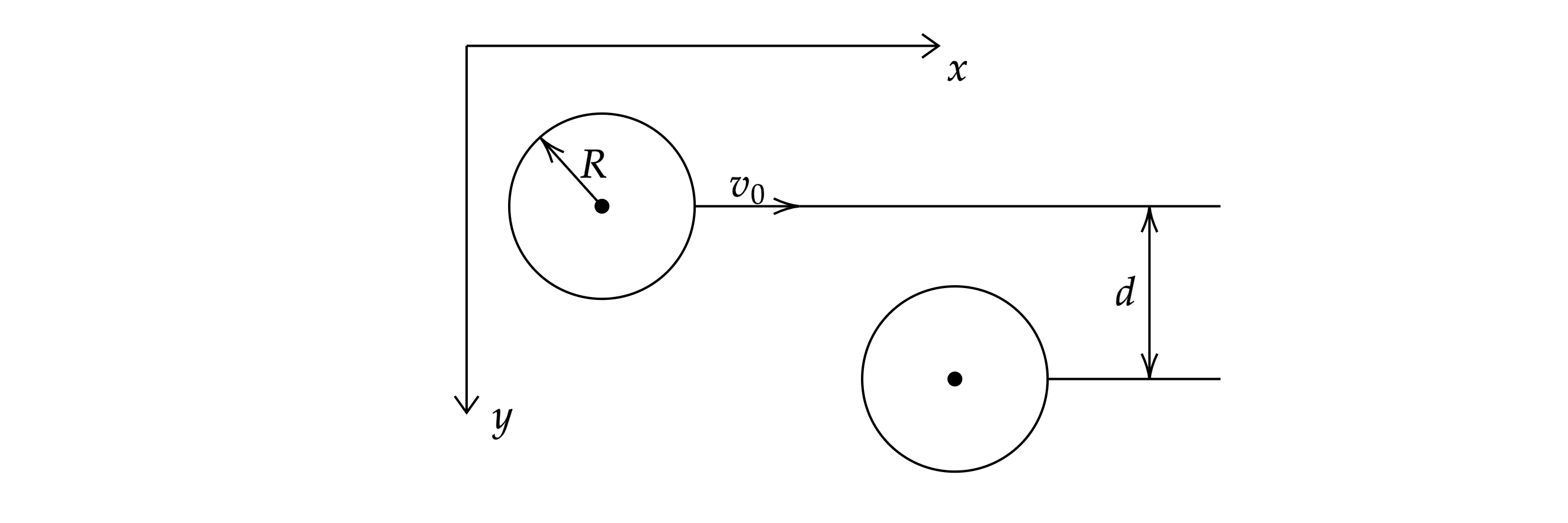
На гладкой горизонтальной поверхности находятся две одинаковые гладкие шайбы радиуса . Одной
из шайб сообщают скорость
вдоль оси
(см. рисунок). При каком значении прицельного
параметра
проекция на ось y скорости второй шайбы после абсолютно упругого удара
максимальна?
(Всеросс., 2015, РЭ, 10)
Источники:
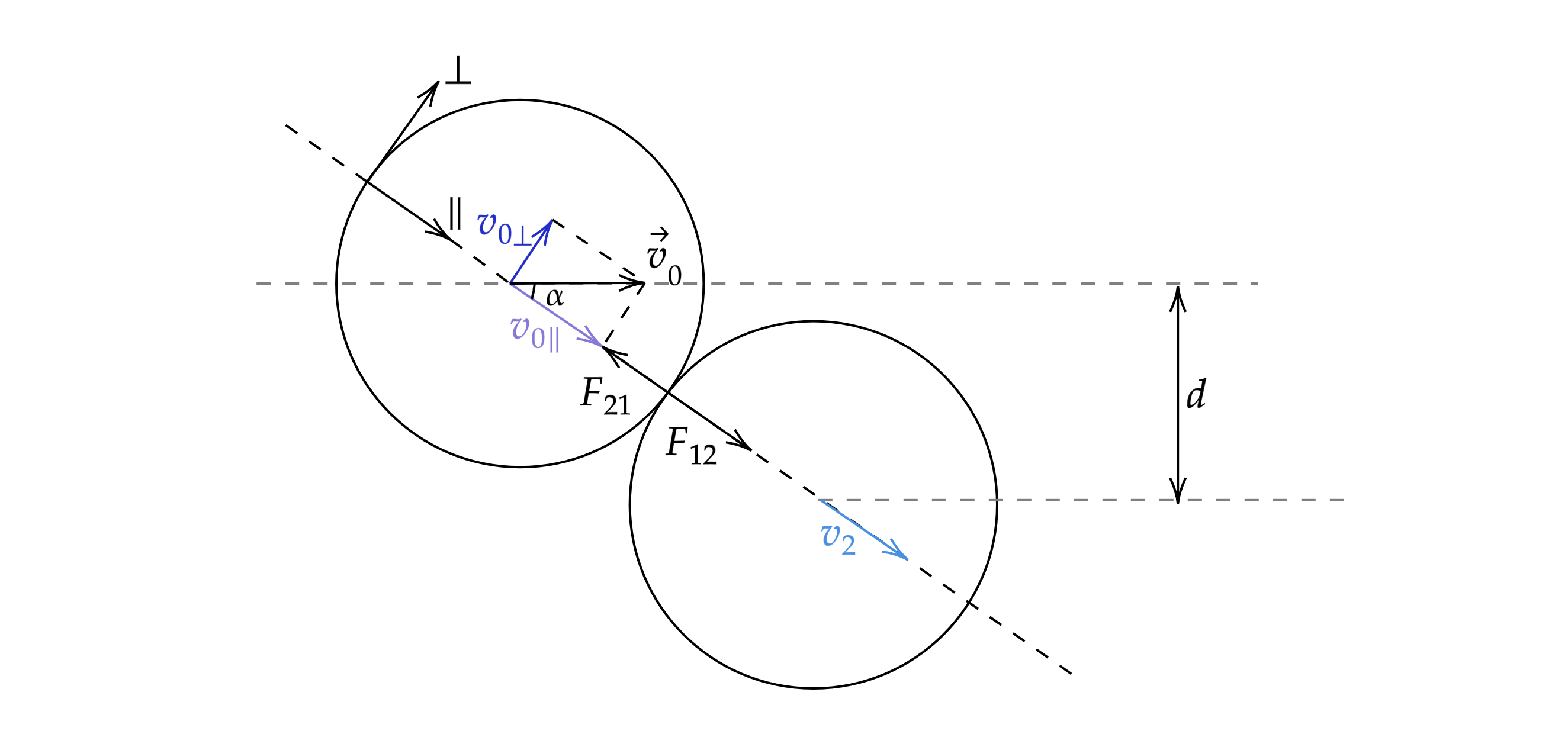
Рассмотрим соударение тел более подробно. Введём оси вдоль линии удара, ось и ось
. Силы в
момент удара направлены только вдоль прямой соединяющей центры шайб (линия удара), это значит,
что второе тело после удара будет двигаться вдоль этой прямой. Докажем, используя ЗСИ и ЗСЭ,
что первая шайба будет двигаться перпендикулярно линии удара. Для этого представим
соударение шайб, как центральный удар вдоль оси
. Тогда ЗСИ на в проекции на ось
:
То есть после удара скорость первой шайбы будет равна , второй
.
Пусть угол между горизонтом и линией удара равен . Тогда проекция скорости второй шайбы:
.
Из треугольника:
Следовательно, проекция будет максимальна при угле в , так как
должен быть равен
1.
Тогда
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




