.03 Закон сохранения и изменения импульса
Ошибка.
Попробуйте повторить позже
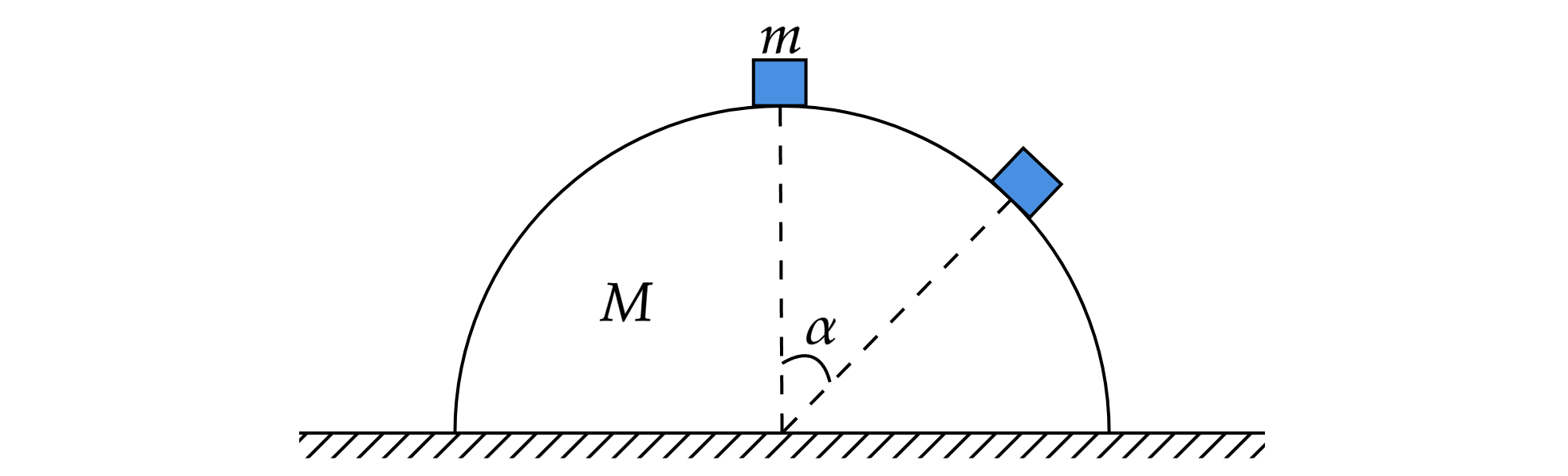
Маленький брусок начинает соскальзывать с вершины гладкой полусферы, стоящей на гладком горизонтальном столе, и в
некоторой точке отрывается от неё. Центральный угол между радиусами полусферы, проведёнными к её вершине и к
точке отрыва, равен .
Найдите отношение массы полусферы
к массе бруска
:
.
(«Курчатов», 2019, 10)
Источники:
Рассмотрим движение бруска и полусферы в инерциальной системе отсчёта, связанной со столом. Ось направим вдоль
стола, ось
вертикально вверх. Так как между полусферой и столом нет трения, то горизонтальная составляющая
полного импульса сохраняется:
Здесь и
– скорости полусферы и бруска относительно стола. По закону сложения скоростей имеем:
– скорость бруска относительно полусферы; вектор
направлен по касательной к окружности, по которой
движется брусок. Получаем:
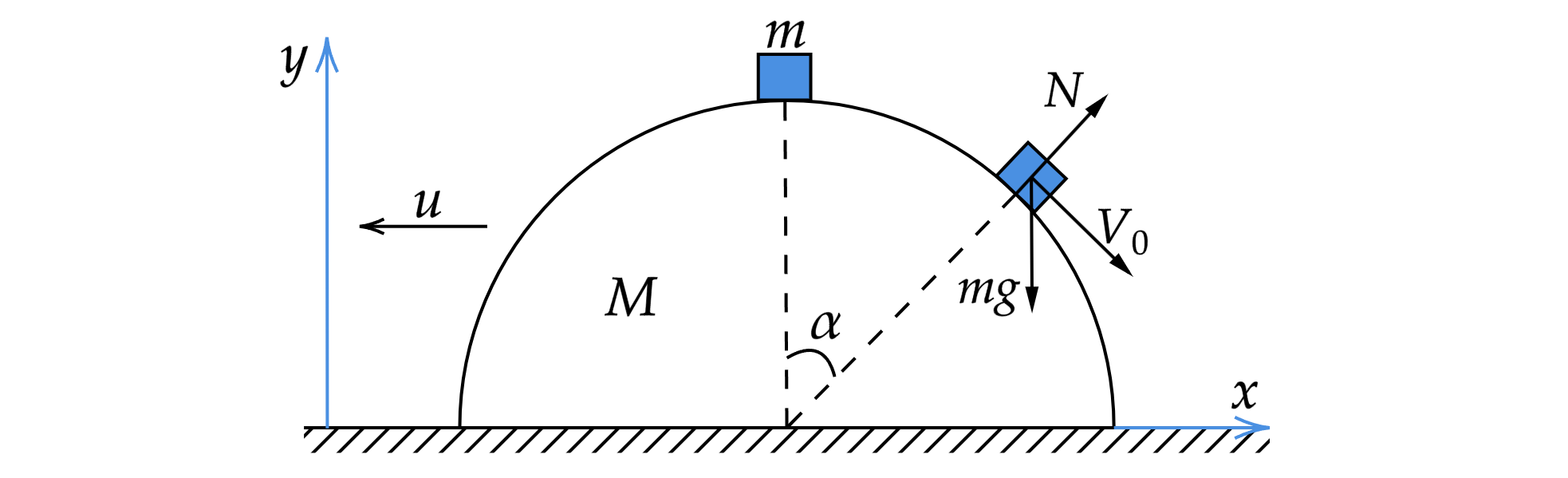
Запишем второй закон Ньютона для бруска:
– ускорение бруска относительно стола,
– сила нормальной реакции, действующая на брусок со стороны
полусферы. По закону сложения ускорений:
– ускорение полусферы относительно стола,
– ускорение бруска относительно полусферы. Вектор
сонаправлен вектору скорости полусферы
. Ускорение
опрелеляется горизонтальной составляющей силы давления
бруска на полусферу. Так как эта сила равна
, то:
В момент отрыва имеем:
Составляющая ускорения , направленная вдоль радиуса полусферы, представляет собой центростремительное
ускорение бруска. Получаем:
радиус полусферы. Для того чтобы найти скорость
, запишем закон сохранения энергии:
Горизонтальная составляющая скорости была найдена выше. Для вертикальной составляющей имеем:
Квадрат скорости равен:
Из закона сохранения энергии получаем:
Далее воспользуемся найденными ранее выражениями для и
:
Отсюда находим отношение масс :
(Официальное решение Курчатов)
| Критерии оценивания выполнения задачи | Баллы |
| Записан закон сохранения горизонтальной составляющей импульса | 1 |
| Записан второй закон Ньютона и закон сложения ускорений | 1 |
| Сформулировано условие отрыва и найдены ускорения бруска и полусферы в момент отрыва | 1 |
| Записан закон сохранения энергии | 1 |
| Получен правильный ответ | 1 |
| Максимальный балл | 5 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




