.02 Абсолютно упругий удар
Ошибка.
Попробуйте повторить позже
Две гладкие упругие круглые шайбы движутся поступательно по гладкой горизонтальной поверхности. Скорости и
шайб непосредственно перед соударением известны и показаны на рисунке. Найдите скорости
и
шайб после
абсолютно упругого нецентрального соударения. Массы шайб
и
.
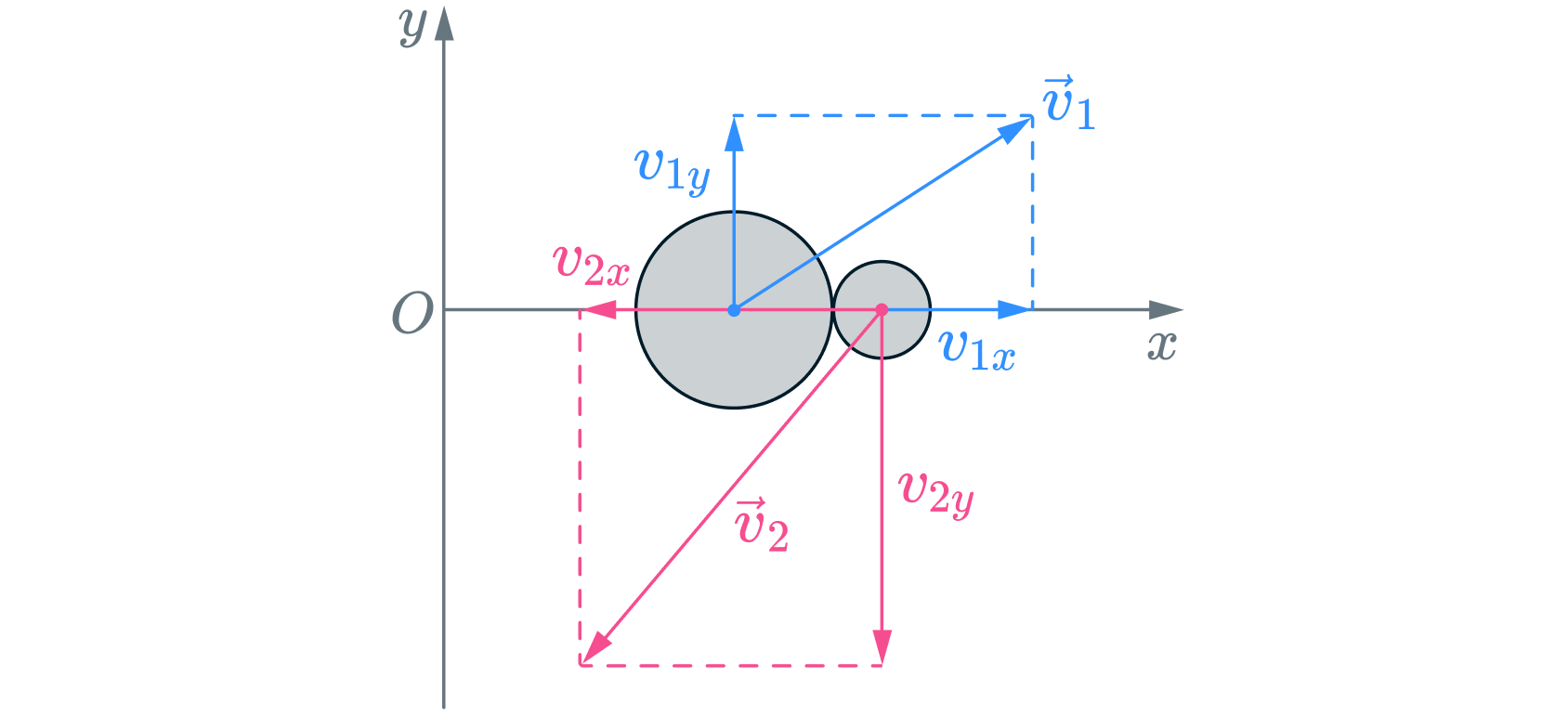
Источники:
Задачу рассмотрим в ИСО, оси координат и
которой лежат в горизонтальной плоскости, при этом ось
направлена по линии центров шайб в момент соударения (см. рис.). В течение времени соударения
на систему шайб действуют только вертикальные внешние силы: это силы тяжести и силы нормальной
реакции. Их сумма равна нулю. Тогда импульс системы шайб в процессе взаимодействия сохраняется:
здесь - импульсы шайб до и после соударения. Так как шайбы идеально
гладкие, то в процессе соударения внутренние силы -силы упругого взаимодействия направлены только по оси
. Эти
силы не изменяют
-составляющие импульсов шайб. Тогда из
,
находим
-составляющие скоростей
шайб после соударения:
т. е. в проекции на ось скорости шайб в результате соударения не изменились.
Найдём -составляющие скоростей шайб после упругого соударения. При таком соударении сохраняется кинетическая
энергия
С учётом равенства -составляющих скоростей шайб до и после соударения последнее равенство принимает
вид:
Обратимся к закону сохранения импульса и перейдём к проекциям импульсов шайб на ось :
Таким образом, исходная задача сведена к задаче об абсолютно упругом центральном ударе: именно такой вид приняли
бы законы сохранения энергии и импульса, если бы скорости шайб были направлены по линии центров. Полученную
нелинейную систему уравнений можно свести к линейной. Для этого следует (как и в предыдущей задаче) в
обоих уравнениях по одну сторону знака равенства объединить слагаемые, относящиеся к первой шайбе,
а по другую - ко второй, и разделить полученные соотношения. Это приводит к линейному
уравнению
Решая систему из двух последних уравнений, находим
Полученные соотношения для и
решают вопрос о проекциях и величинах скоростей шайб после
соударения
а также об углах и
, которые векторы скорости
и
образуют с положительным направлением оси
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




