6.10 Задачи повышенного уровня сложности
Ошибка.
Попробуйте повторить позже
Найдите все отрицательные значения при которых прямая
пересекает
в двух точках ломаную, заданную условиями:
При имеем
, то есть
— место сгиба ломаной. Изобразим
график ломаной:
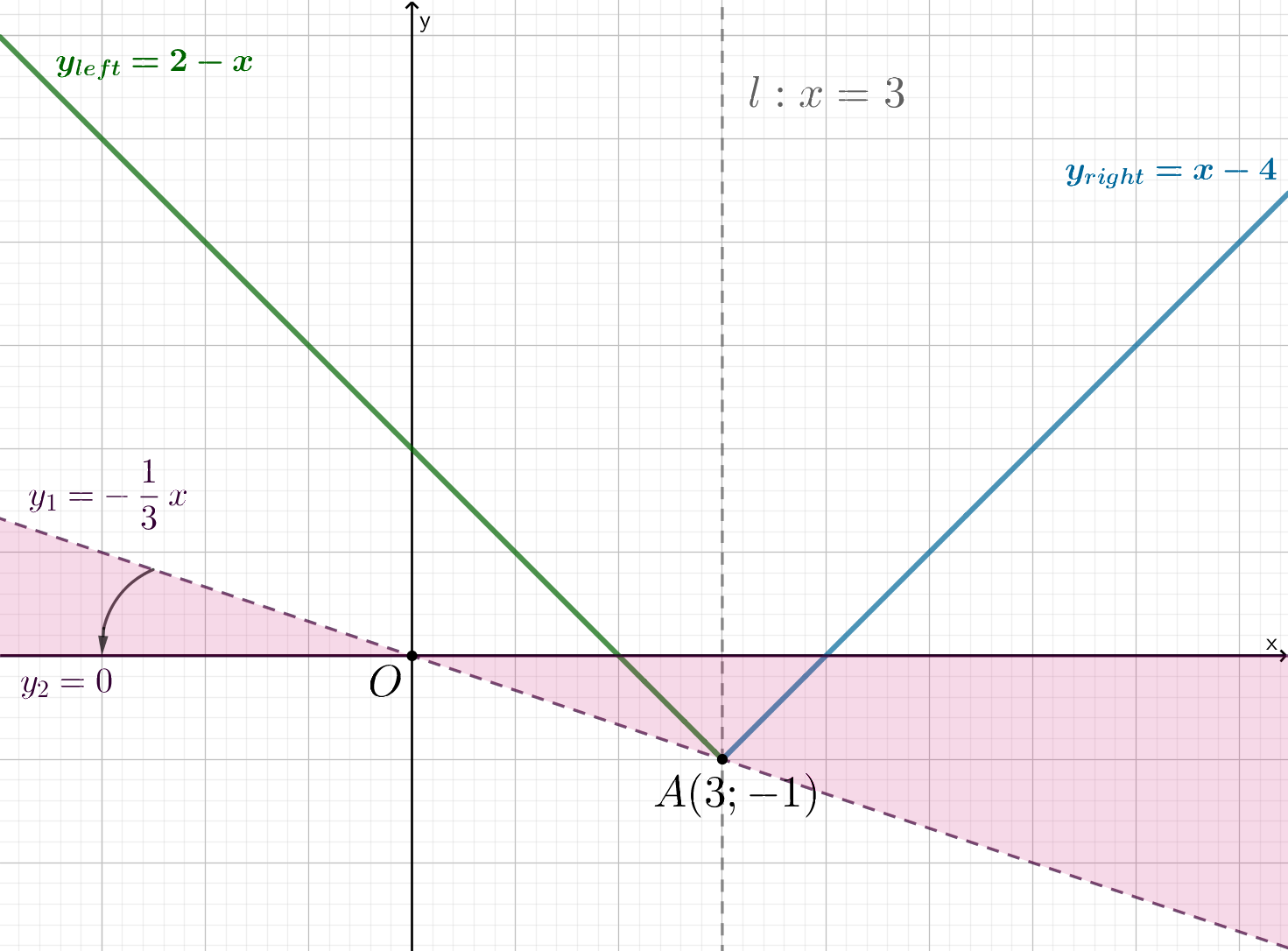
Прямая проходит через начало координат
и находится во II и IV
четвертях. Изменяя
от
до
прямая
вращается против часовой
стрелки. Вращая так прямую, находим граничное положение прямой:
, которая
проходит через точку
и имеет с ломаной одну общую точку. Двигаясь дальше
против часовой стрелки, все получаемые прямые уже будут иметь две общие точки
с ломаной вплоть до прямой
(все прямые, находящиеся в области,
обозначенной розовым цветом).
Так как , то
, откуда
, следовательно,
.
Значит, ответ:
| Критерии оценивания выполнения задания | Баллы |
| График построен верно, верно найдены искомые значения параметра | 2 |
| График построен верно, но искомые значения параметра найдены неверно или не найдены | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




