Планиметрия на ОММО
Ошибка.
Попробуйте повторить позже
Векторы , расположенные в одной плоскости с вектором
, имеют равную длину, отличную от длины вектора
. Известно,
что
Найдите
Источники:
Подсказка 1
Давайте выразим всё через a₁ и a₃, ведь именно они выделяются: a₁ = 4/9 * a₂ + 5/9 * b, a₃ = 9/16 * a₄ + 7/16 * b. Что мы можем заметить здесь? А если вспомнить словосочетание «отношение отрезков»?
Подсказка 2
Это похоже на то, что мы взяли вектора a₂ и b, провели их от одной точки и на отрезке, который соединяет их концы, поставили точку с отношение 7/9, и вот этот вектор равен a₁. Аналогично с a_3. Как теперь можно наше наблюдение совместить с фактом про равные длины из условия?
Подсказка 3
Давайте создадим треугольник AOE, где OA = a₂, OE = b. Тогда вектор a₁ понятно находится по рассуждению выше. Но ведь у нас еще есть a₃. Пусть тогда OD = a₄. Тогда, опять же, a₃ понятно ищется на картинке. Но что же все таки с равными длинами? В какой конструкции у нас много точек на одном расстоянии лежит?
Подсказка 4
Верно! Концы векторов a₁, a₂, a₃, a₄ лежат на одной окружности, при этом прямые DC, AB, OE пересекаются в одной точке и делятся понятным отношением этой самой окружностью. Что тогда остается сказать, если даны окружность и отношения секущих?
Подсказка 5
Можно сказать, что у нас EB * EA = EC * ED, если BA = 4x, а EC = 9y, то y = x/2. Осталось воспользоваться условием задачи ещё раз
Выразим и
. Поэтому
— чевиана в треугольнике
со сторонами
и
, которая
делит третью сторону
в отношении
к
. А
— чевиана треугольника
со сторонами
и
, делящая
в
отношении
к
. Так как векторы
равны, то они лежат на окружности с центром в точке
, а треугольники
и
— равнобедренные.
![]()
По теореме об отрезках секущих
Откуда
По условию , следовательно
Ошибка.
Попробуйте повторить позже
Дана трапеция с основаниями
и боковыми сторонами
. Точка
на прямой
такова, что
периметр треугольника
наименьший из возможных. Найдите этот периметр.
Источники:
Подсказка 1
Заметим, что основание у нашего треугольника зафиксировано. То есть на самом деле нам нужно найти минимальную сумму расстояний до точки P от A и B. Давайте попробуем понять, почему расстояние будет минимальным, когда лучи PA и PB будут падать под одним углом на BC. Обычно когда речь идёт о минимуме или максимуме, то нужно неравенство, а в геометрии чаще всего — это неравенство треугольника. Как можно попробовать сделать из отрезков PA и PB треугольник, в котором мы явно будем видеть их сумму?
Подсказка 2
Верно, хоть до этого и не просто догадаться, давайте попробуем отразить точку D симметрично относительно BC. Что тогда у нас получается? Пусть симметричная точка X. Получается треугольник APX, где сумма наших расстояний это AP+PX. Но тогда записав неравенство треугольника, когда достигается минимум?
Подсказка 3
Да, получается, чтобы сумма расстояний выстроилась в одну прямую, а это и будет минимум по неравенству треугольника, нужно как раз равенство углов. Победа! Теперь осталась только техническая часть поиска двух сторон равнобедренного треугольника APD. Это можно сделать, например, через теорему Пифагора для половины основания, высоты и стороны треугольника. Нужно только найти высоту трапеции, что при наличии стольких данных несложно.
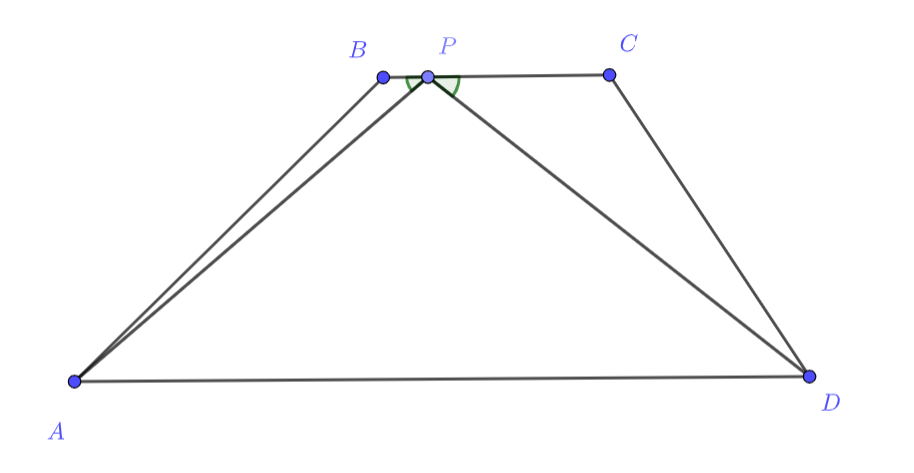
Первое решение.
Воспользуемся следующим утверждением, которое наиболее известно как «принцип наименьшего времени Ферма» в физике:
Для данных точек и данной прямой
из всех точек
сумма
будет минимальной, когда углы между прямыми
и
и
и
будут равны.
Тогда для искомой точки на прямой
должно выполняться равенство
(точки
и
- где-то «далеко» на
прямой
. Поскольку
, то
т.е. треугольник - равнобедренный. Значит, нам достаточно найти периметр равнобедренного треугольника
, где
- точка
на прямой
.
По теореме Пифагора этот периметр равен
где - расстояние между прямыми
и
, т.е. высота трапеции.
Найти высоту трапеции можно разными способами. Например, проведём через точку , прямую, параллельную
, до пересечения с
основанием
в точке
. Тогда искомая высота - это высота из вершины
в треугольнике
. Поскольку
параллелограмм, то
,
.
Итого, нам достаточно найти длину высоты на сторону длины 7 в треугольнике со сторонами 5 , . По формуле площади и
формуле Герона имеем
откуда
и окончательный ответ .
Второе решение.
Также, как и в первом решении, найдём высоту трапеции. Покажем здесь, как можно это было сделать по-другому. Опустим высоты
и
трапеции. Обозначим их длины через
, длину отрезка
обозначим через
. Поскольку
, для
получим
. Из прямоугольных треугольников
и
по теореме Пифагора получим
и
Подставив в эти равенства известные длины, получим систему уравнений
Вычитая из первого равенства второе, получим , откуда
. Тогда
.
Рассмотрим треугольник . Обозначим
, тогда
(здесь и далее все расстояния со знаком, т.е. могут быть
отрицательные). Опустим высоту
. Тогда треугольник
прямоугольный и по теореме Пифагора
Аналогично, из прямоугольного треугольника
Тогда периметр треугольника равен
Найдём производную этой функции:
Из уравнения получаем
откуда . Несложно видеть, что
именно точка минимума, откуда минимальный периметр равен
.
Ошибка.
Попробуйте повторить позже
В треугольнике точки
— середины сторон
а
,
— точки касания этих сторон со вписанной
окружностью соответственно. Прямые
пересекают
в точках
и
Докажите, что прямая
делит отрезок
пополам.
Источники:
Подсказка 1
Один отрезок делит другой пополам, часто это происходит потому что они являются диагоналями некоторого параллелограмма.
Подсказка 2
В данном случае окажется, CXC1Y - параллелограмм, но нужно как-то подобраться к точкам X и Y...
Подсказка 3
В этом нам поможет лемма 255, согласно ней точки X и Y лежат на биссектрисах углов A и B соответственно.
Докажем, что точки лежат на биссектрисах углов
соответственно (это утверждение известно как задача
и может быть
использовано на олимпиаде без доказательства). Так как
и
то
следовательно,
и
Аналогично
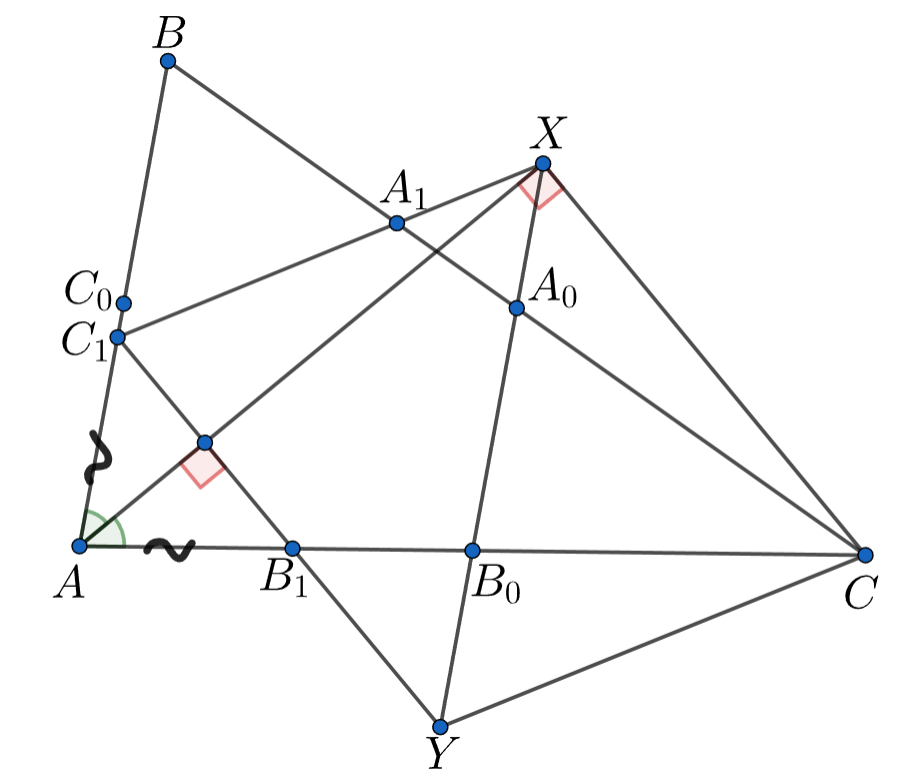
Итак, по лемме
и
потому что треугольник
равнобедренный и
в нём биссектриса,
проведённая к основанию. Следовательно,
Аналогично
Таким образом, четырёхугольник
—
параллелограмм. В таком случае его диагонали точкой пересечения делятся пополам, это даёт нам требуемое.
Ошибка.
Попробуйте повторить позже
Точка является центром окружности, описанной около треугольника
со сторонами
и
. Найдите длину стороны
, если длина вектора
равна
.
Источники:
Подсказка 1
В таких задачах на счет нужно очень четко понять, какие переменные мы вводим и зачем это делать. Какие переменные у нас уже известны? Две стороны треугольника. Значит, если попробовать выразить наше выражение векторное, через часть из известных переменных и того, что нам нужно найти, то может что-то получится.
Подсказка 2
Давайте выразим каждый из векторов в выражении через векторы CA и AB, тогда выходит, что |3AC + AB| = 10 (здесь написаны векторы). Далее, нам ничего не остается как возводить в квадрат, но там вылезет косинус из произведения векторов. Как побороть эту проблему, если у нас в виде переменных остаются AB и cos(BAC).
Подсказка 3
Конечно, у нас есть cos(BAC) и AB, значит все намекает на теорему косинусов для треугольника ABC и стороны BC. Вычтя из нашего равенства, которое получилось возведением в квадрат модуля, равенство из теоремы косинусов, получим уравнение, в котором есть AB*cos(BAC), приравненное к константе. Что тогда можно сделать, чтобы найти AB?
Подсказка 4
Само собой, остается подставить это в уравнение, полученное из модуля, так как после подстановки, там останется одна неизвестная - AB, а значит, задача решена!
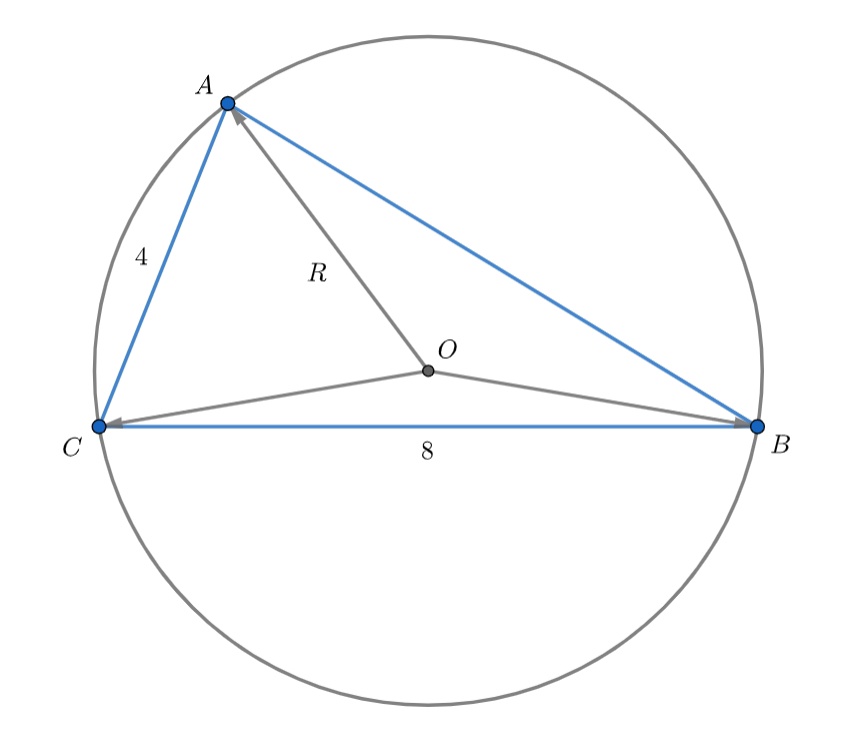
Будем пользоваться тем, что скалярный квадрат вектора равен квадрату длины вектора.
Из условия получаем, что
то есть
то есть
А теперь возведём обе части в квадрат:
По теореме косинусов из треугольника имеем
Вычитая это равенства из полученного выше, получаем:
С учётом имеем:
Итак,
Ошибка.
Попробуйте повторить позже
В треугольнике сторона
Биссектриса
делится точкой пересечения биссектрис треугольника в отношении
считая от вершины. Найдите длину стороны
если радиус вписанной в треугольник
окружности равен
14.
Источники:
Подсказка 1
Вот у нас есть уже одна биссектриса и центр вписанной окружности. Попробуйте рассмотреть биссектрису из точки A, но только не в треугольнике ABC, а в треугольнике ALC) Чем здесь можно воспользоваться?
Подсказка 2
Например, свойством биссектрисы про отношение сторон) Из этого будет следовать, что AL = 21. Теперь попробуйте понять, как можно выразить синус угла A..
Подсказка 3
Различным выражением площади треугольника ALC) Ведь с одной стороны это просто формула площади через синус и две стороны, а с другой стороны, можно разбить треугольник на два: AIC и AIL. Но как удобнее найти их площади?
Подсказка 4
Площадь каждого можно найти с помощью радиуса вписанной окружности и сторон, ведь в этих треугольниках радиусы будут высотами!Так, мы находим синус А = 1, т.е. угол А прямой) А дальше просто обычный счет и использование свойства биссектрисы снова)
Пусть — центр вписанной в треугольник
окружности (т.е. точка пересечения биссектрис). Заметив, что
— биссектриса, в
треугольнике
в силу свойства биссектрисы треугольника имеем:
Далее,
где — радиус вписанной в треугольник
окружности. Таким образом,
В силу свойства биссектрисы треугольника
имеем
Полагая имеем
В силу теоремы Пифагора:
Ошибка.
Попробуйте повторить позже
В треугольнике длины сторон равны
,
и
. Найдите площадь фигуры, состоящей из тех и только тех точек
внутри
треугольника
, для которых выполняется условие
Источники:
Подсказка 1
Расстояния между точками удобно считать, когда есть система координат. Как было бы удобно расположить наш треугольник в декартовой системе координат?
Подсказка 2
Заметим, что высота, проведенная к стороне длины 4, равна целочисленному числу, поэтому удобно ввести систему координат так, чтобы Оу было вдоль этой высоты, а Ох — вдоль упомянутой стороны треугольника. Тогда координаты вершин треугольника принимают целочисленные значения.
Подсказка 3
Пусть (x; y) — координаты X. Тогда выражение XA² + XB² + XC² можно представить как сумму двух квадратов с некоторыми коэффициентами, что очень напоминает уравнение окружности с центром в (x; y). А так как нам дано неравенство, то наша фигура в X — это круг! Останется лишь показать, что все его точки лежат внутри △ABC.
Первое решение. Обозначим .
Докажем утверждение, известное как теорема Лейбница в геометрии. Пусть - точка пересечения медиан треугольника
.
Представим
тогда
Поскольку центр тяжести треугольника
, то
и
С учётом доказанной выше теоремы задача эквивалентна
то есть неравенство сводится к
Итак, геометрическим местом точек , удовлетворяющих поставленному условию, является круг радиуса
с
центром в точке пересечения медиан треугольника
.
Этот круг принадлежит треугольнику, если его радиус не больше, чем одна треть наименьшей из высот :
Значит, при выполнении условия
искомая площадь равна . По формуле Герона найдем площадь треугольника:
Вычислим
Поскольку , условие
выполняется:
Значит, ответ: .
Второе решение. Высота треугольника, проведенная к стороне длины , равна
. Основание высоты делит эту сторону на отрезки,
равные
и
. Введем систему координат так, как показано на рисунке. Тогда
.
![]()
Перепишем неравенство
так:
Оно определяет круг радиуса с центром в точке
. Покажем, что все точки этого круга принадлежат треугольнику
. Для этого найдем расстояния от точки
до сторон треугольника. Уравнение стороны
, расстояние до неё
равно
. Уравнение стороны
, расстояние
. И
расстояние от точки
до стороны
равно, очевидно,
. Наименышее из расстояний
, тем не менее, больше,
чем радиус круга
. Поэтому весь круг и является той фигурой, площадь которой требуется найти, откуда
.
Ошибка.
Попробуйте повторить позже
Дан равнобедренный треугольник с углом при вершине, равным
. Точка
расположена внутри треугольника
так, что
, а
. Найдите величину угла
.
Источники:
Подсказка 1
У нас есть три пересекающиеся в одной точке(хоть и не продолженные до пересечения со сторонами) чевианы, а значит, мы можем записать тригонометрическую теорему Чевы. Но вот загвоздка, нам надо будет решать тригонометрическое уравнение вида sin(114 - x) * a = b * sinx, где a и b - некоторые константы. Но если, скажем, мы хотим просто угадать корень, то какие претенденты есть?
Подсказка 2
Вот у нас там будут константы в числителе sin3 * sin27, а в знаменателе sin30 * sin6. Ну как будто хотелось бы не расписывать громоздко sin27, чтобы не портить произведение, при этом как-то
Первое решение.
Пусть — высота/медиана/биссектриса треугольника. Пусть
— пересечение луча
и отрезка
.
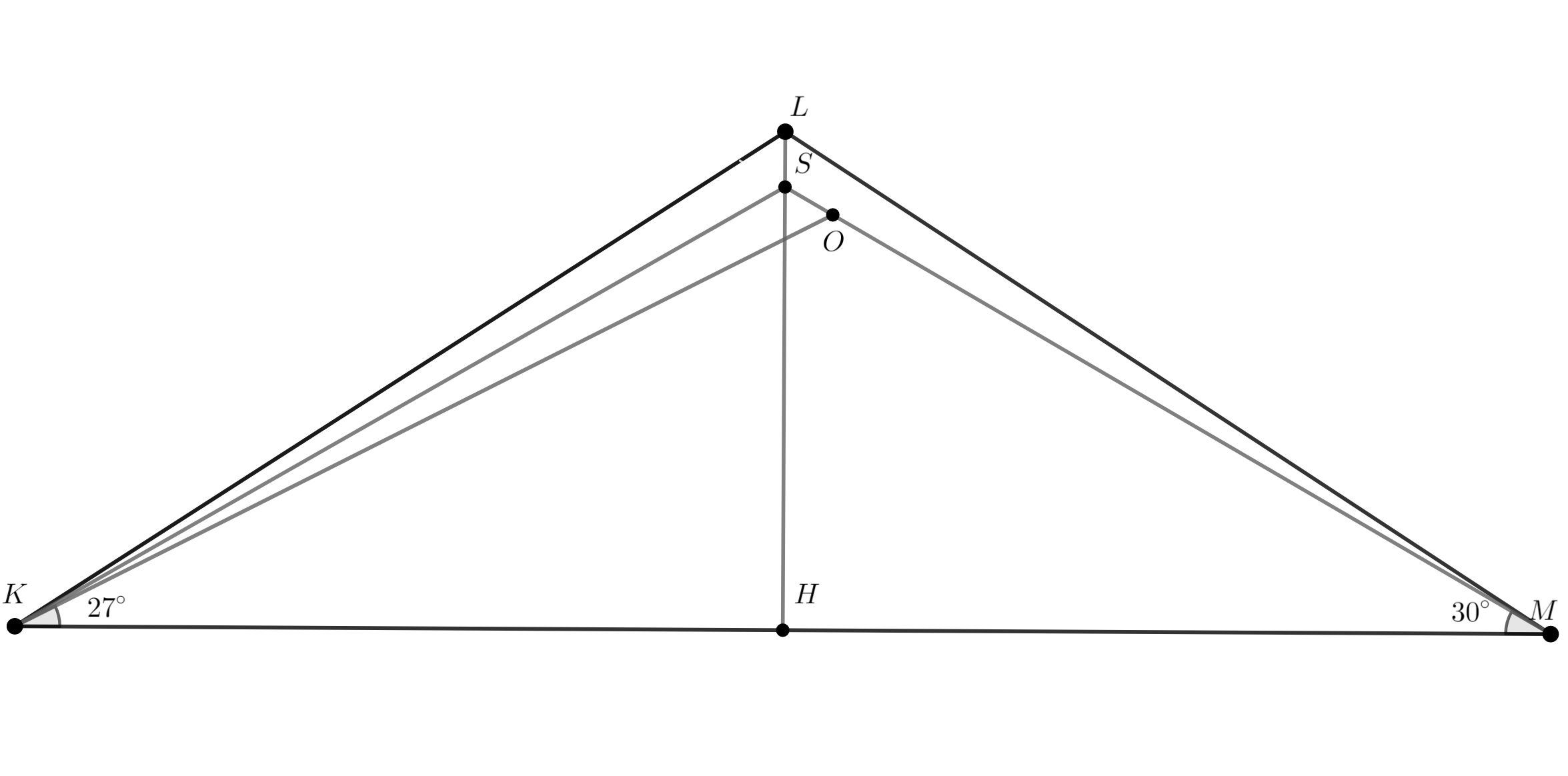
Заметим, что (поскольку в треугольнике
медиана
совпала с высотой).
Посчитаем углы: 1. ; 2.
; 3.
; 4.
;
5.
, а значит
; 6.
, а значит
.
Треугольники и
равны по общей стороне
и двум углам (пункты 5. и 6.) Следовательно,
, треугольник
равнобедренный. Значит,
________________________________________________________________________________________
Второе решение.

Несложно посчитать, что . Докажем, что
, а
. Для этого воспользуемся
тригонометрической формой теоремы Чевы. В соответствии с этой теоремой нам достаточно проверить, что
или . Это очевидно:
Осталось лишь вычислить из треугольника
.
Ошибка.
Попробуйте повторить позже
В прямоугольном треугольнике на катете
как на диаметре построена окружность, которая пересекает гипотенузу
в точке
. Через точку
проведена касательная к окружности, которая пересекает катет
в точке
. Найдите длину
, если
,
а
.
Источники:
Подсказка 1
В условии фигурирует касательная, очень часто помогает искать какие-то углы, образованные ею) Также не зря окружность построена на AC, как на диаметре: можно поискать какой-то удобный угол, после чего делать какие-то выводы!
Подсказка 2
Т.к. AC является диаметром новой окружности, угол CEA прямой. Угол между касательной и хордой равен вписанному углу, опирающемуся на эту хорду, поэтому углы CED и A равны.
Подсказка 3
Хотим поискать еще каких-то углов в треугольнике CEB, чтобы найти DB, в этом должен помочь небольшой подсчёт углов) А так же стоит подумать, чем же является DE для треугольника BEC! Не забываем о том, как же искать высоту в прямоугольном треугольнике ABC)
.png)
Угол между касательной и хордой равен вписанному углу, опирающемуся на эту хорду, поэтому . Так как
как
вписанный угол, опирающийся на диаметр
, то
.
Отсюда следует, что равнобедренный:
. Ещё равнобедренным является треугольник
, ведь мы поняли, что
. Делаем вывод
.
При этом высота прямоугольного треугольника равна среднему геометрическому отрезков гипотенузы, то есть .
В итоге получаем
.
Ошибка.
Попробуйте повторить позже
Дан треугольник . На отрезках
и
выбраны точки
и
соответственно так, что
. Оказалось, что точки
и
лежат на одной окружности. Пусть
— биссектриса треугольника
на отрезке
. Докажите, что
.
Источники:
Подсказка 1
Подумаем, как можно доказать параллельность...нам даны биссектрисы, 4 точки на одной окружности, равные отрезки... на какую теорему, связанную с отрезками и параллельностью это всё намекает?
Подсказка 2
Это всё намекает на отношения, а они - на теорему Фалеса. Попробуем записать отношения, связанные с окружностью(отрезки секущих) и связанные с биссектрисой и как-то записать цепочку неравенств. Ясно, что когда-то в этой цепочке придём к замене BY на AX, а прийти хотим к таким отношениям, чтобы напрямую воспользоваться теоремой Фалеса для прямых XL и BC!
.png)
Из того, что точки и
лежат на одной окружности, следует, что
, или
. Из того, что
- биссектриса треугольника
следует, что
. Тогда
откуда по теореме, обратной теореме Фалеса, получаем, что , что и требовалось.
Ошибка.
Попробуйте повторить позже
В трапецию вписана окружность, касающаяся боковой стороны
в точке
. Найдите площадь трапеции, если
и
.
Источники:
Подсказка 1
Для начала подумаем, а какие данные нам нужны, чтобы найти площадь трапеции? Быть может, мы можем найти какие-то отрезки, если правильно воспользоваться информацией о касательных к вписанной окружности? Возможно, какая-то новая информация может показаться нам лишней, но условие кажется очень маленьким, поэтому любые новые знания нам нужны) Как же всё-таки воспользоваться длинами DK, CD и AK?
Подсказка 2
Отрезки касательных к одной окружности, проведенные из одной точки, равны! Это значит, например, что можно как-то обозначить все точки касаний окружности и сторон трапеции и найти почти все отрезки, на которые точки касания делят стороны) Теперь у нас есть одно из оснований, часть другого, нужна высота... Что же на нашем рисунке может намекать на перпендикулярность(связанное с окружностью)? Что для этого нужно отметить?
Подсказка 3
Вспоминаем, что некоторые радиусы вписанной окружности перпендикулярны сторонам. Тогда отметим у окружности центр I и опустим радиусы на каждую из сторон. Понятно, что радиусы на основания образуют высоту, т.е. теперь достаточно найти радиус. Для этого нам понадобится найти IK (перпендикуляр IK опущен на сторону, у которой мы знаем длины обоих отрезков). Какой факт о DI и AI можно использовать?
Подсказка 4
DI перпендикулярен AI! Тогда в прямоугольном треугольнике DIA мы можем найти высоту IK (из различных подобий), т.е. радиус. Аналогично можно поступить с прямоугольным треугольником CIB, тогда мы найдем еще один отрезок касательной, т.е. нам уже известна высота (2 радиуса) и оба основания, а, значит, и высота) Главное не ошибиться в счёте!
Первое решение.
Пусть точки касания с и
будут
и
соответственно. Из равенства отрезков касательных
и
, а также
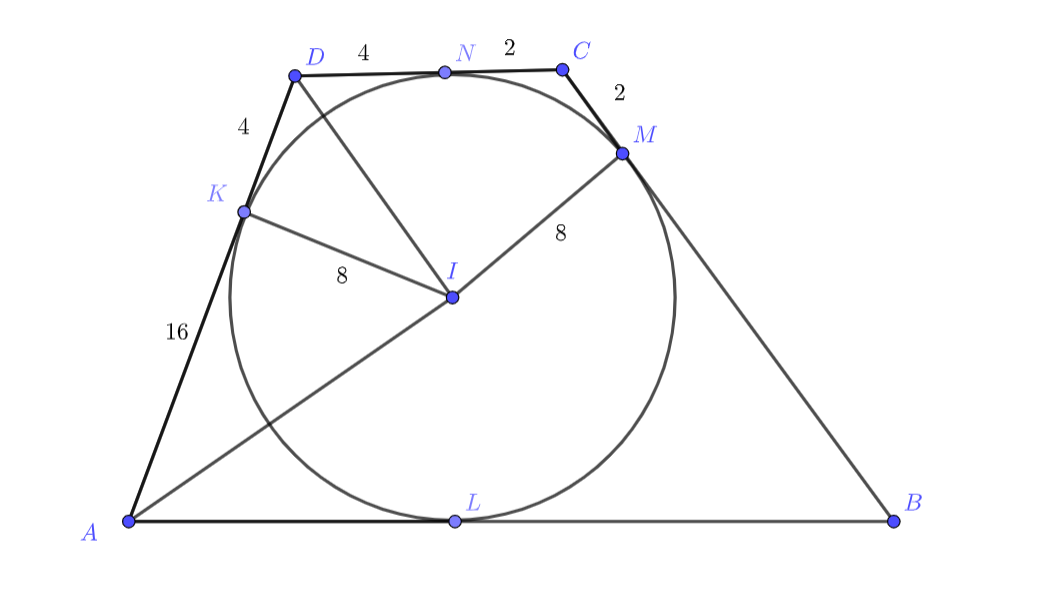
Как известно, , как биссектрисы углов трапеции, но тогда
— высота прямоугольного треугольника и равна
. Аналогично из прямоугольного
имеем
. Откуда легко посчитать, что
.
Второе решение.
Пусть — точка касания окружности и стороны
Так как
и
— отрезки касательных, то они равны. Значит,
Пусть — точка касания окружности и стороны
Аналогично
Пусть — точка касания окружности и стороны
Проведем диаметр
и опустим высоту
на сторону
(как отрезки касательных), следовательно,
и
Тогда по теореме
Пифагора
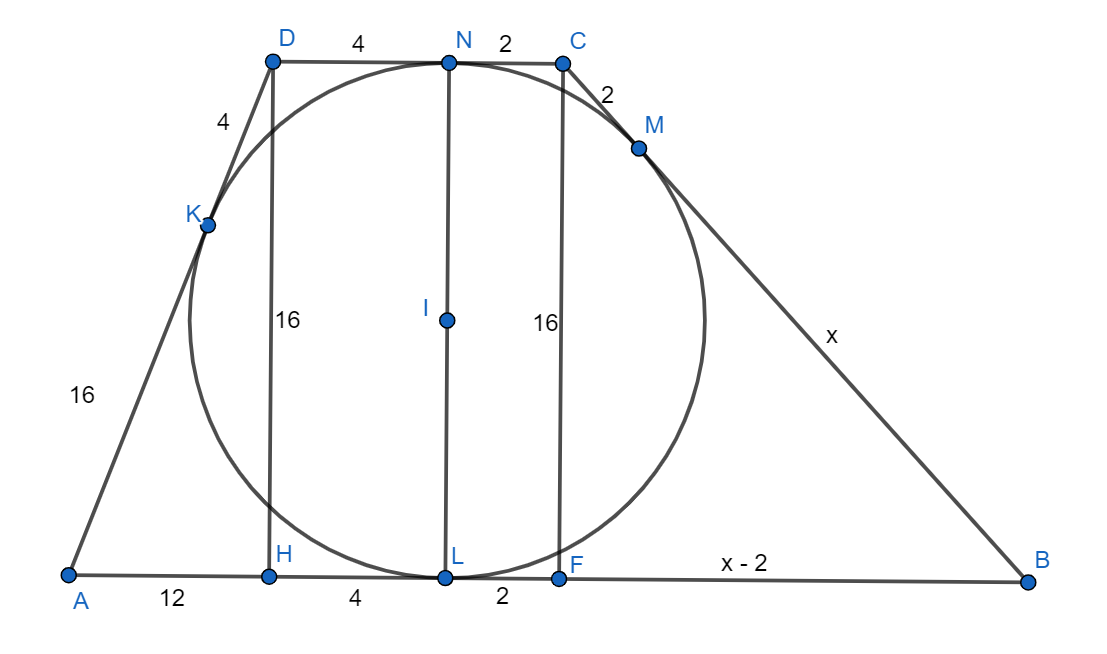
Опустим из точки перпендикуляр
на сторону
он будет равен
Обозначим за
отрезок
тогда
По теореме Пифагора
Тогда
Ошибка.
Попробуйте повторить позже
Точки — точки пересечения продолжений высот остроугольного треугольника
с описанной вокруг
окружностью.
Окружность, вписанная в треугольник
, касается одной из сторон
, а один из углов треугольника
равен
. Найдите
два других угла треугольника
Источники:
Подсказка 1
С помощью свойств ортоцентра докажите, что H - инцентр A_1 B_1 C_1
Подсказка 2
Нужно доказать, что треугольник H B C_{1} --- равносторонний.
Первое решение.
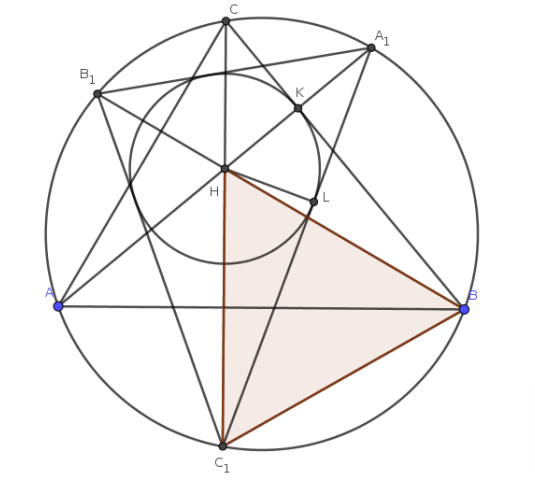
Не умаляя общности, пусть окружность , вписанная в
, касается стороны
. Пусть
- точка пересечения высот
треугольника
- точка касания
и
точка касания
и
Известно, что высоты являются биссектрисами его ортотреугольника. При гомотетии с центром в точке
и
коэффициентом
ортотреугольник переходит в
так что биссектрисы
тоже пересекаются в точке
По свойству ортоцентра и
симметричны относительно прямой
, так что
Кроме того,
(
), поэтому прямоугольные треугольники
и
равны по катету (
) и
острому углу. Поэтому
В итоге получили Тогда
, откуда с учётом условия и следует ответ.
Второе решение.
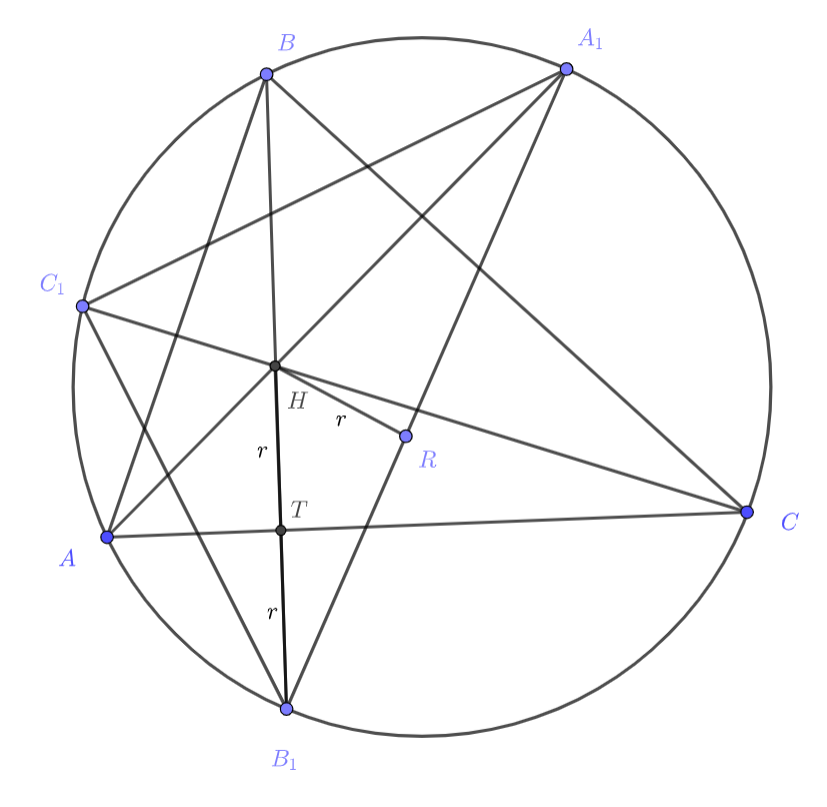
Пусть высоты пересекаются в точке
. Заметим, что
Отсюда следует, что лежит на биссектрисе угла
. Делая то же самое для остальных углов, имеем, что
— центр вписанной
окружности
Обозначим радиус этой окружности за и, не умаляя общности,
(касание из условия). Нетрудно видеть,
что
является высотой треугольника
. Поскольку мы уже знаем, что
(
— также биссектриса
), то
(получили высоту и биссектрису
). Пусть также
точка касания вписанной окружности. Тогда в прямоугольном
катет равен половине гипотенузы и
. Поскольку мы знаем, что какой-то другой угол
равен
, то третий будет
и
Ошибка.
Попробуйте повторить позже
Пусть — точка пересечения диагоналей
и
правильного шестиугольника
со стороной
Точка
такова, что
Определите, лежит ли точка
внутри, на границе или вне
а также найдите длину отрезка
Источники:
Подсказка 1
Заметим несколько фактов: в правильном шестиугольнике CE перпендикулярно FE и AB при проекции на EF или CB равняется EF/2. Попробуйте использовать эти два факта!
Подсказка 2
Пусть К' - точка пересечения AB и CE. Теперь мы можем использовать вектор CK' для выражения, попробуем найти равный ему вектор!
Подсказка 3!
Верно, это LK! Осталось правильно применить все полученные на рисунке векторы!
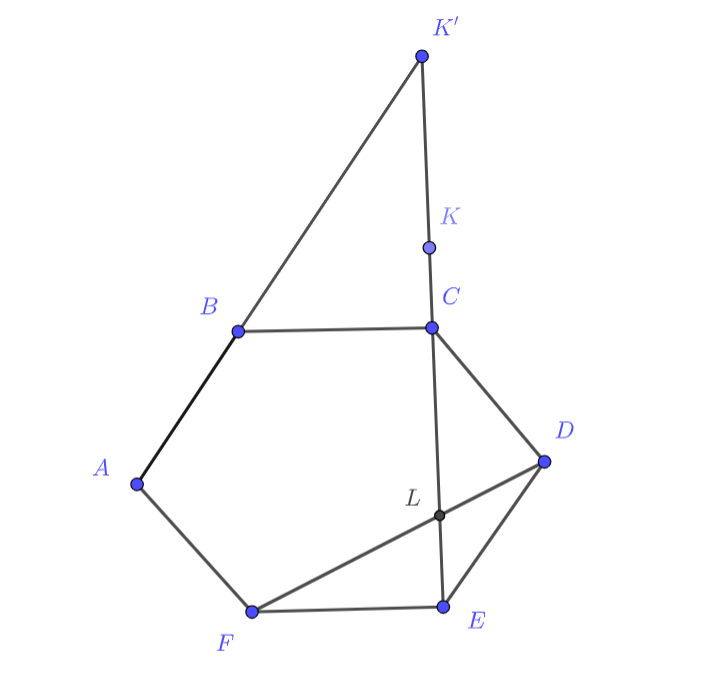
Как известно, а также проекция
на прямую
равна
Поэтому если продлить
в три раза до точки
то
(удвоенная проекция
равна
). Отсюда легко видеть, что
то есть
По свойствам
правильного шестиугольника
В итоге
Вне,
Ошибка.
Попробуйте повторить позже
Пусть — диаметр окружности
,
— окружность с центром в точке
и радиусом меньше, чем у
. Окружности
и
пересекаются в точках
и
. Хорда
окружности
пересекает вторую окружность
в точке
. Найдите длину отрезка
,
если
.
Источники:
Подсказка 1
Давайте продлим отрезок OB до пересечения с окружностью ω и назовём точку их пересечения N, аналогично продлим DB и назовем их точку пересечения M. Что тогда можно сказать про углы ABC, DBA и MBN?
Подсказка 2
Дуги OC и OD равны в силу симметрии относительно диаметра OP. Значит, ∠ABC = ∠DBA, а ∠DBA и ∠MBN равны, как вертикальные. Что тогда можно сказать про точки M и C, а также отрезки BC и BM?
Подсказка 3
Точки M и C симметричны относительно перпендикуляра к AB, проходящего через точку B, следовательно, отрезки BC и BM будут равными. По условию нам дано CB*BD = 5, следовательно, MB*BD = 5. На какую теорему нам сразу же намекает такое произведение?
Подсказка 4
Когда мы видим произведение отрезков одной хорды, то сразу же нужно вспомнить теорему о пересекающихся хордах, запишем её: MB*BD = AB*BN. Отлично, теперь у нас появилось нужное нам AB, но также появился отрезок BN, про который нам ничего неизвестно. Подумайте, как можно заменить BN?
Подсказка 5
Давайте заметим, что треугольник APN – равнобедренный, а ∠ABP = 90°, в таком случае отрезок PB является высотой и медианой, а BN = AB.
Пусть и
– вторые точки пересечения с окружностью
прямых
и
соответственно. В силу симметрии относительно
прямой
, дуги
и
равны. Следовательно,
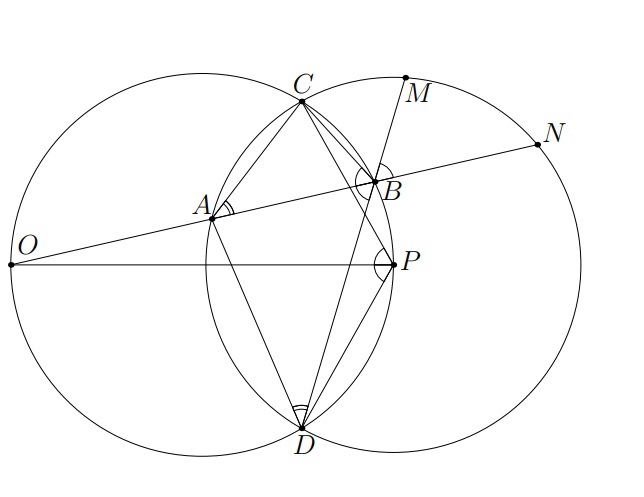
Первое решение.
Обозначим эти равные углы через . Из вписанности четырёхугольника
получаем, что
. Следовательно,
поскольку
– центр
, имеем
C другой стороны,
. Вычитая общую дугу
,
получаем, что
, откуда
Значит, , и треугольники
и
подобны по двум углам, откуда
, так что
______________________________________________________________________________________________________________________________________________________
Второе решение.
Заметим, что , как вписанный угол в окружности
, опирающийся на её диаметр
, поэтому
является высотой и
биссектрисой треугольника
. Получаем, что точки
и
симметричны относительно прямой
, так что
В
окружности
по теореме о пересекающихся хордах
Тогда
откуда сразу получаем
ответ.
_________________________________________________________________________________________________________________________________________________________________________________
Замечание.
В ходе первого решения мы выяснили, что . То есть прямые
и
симметричны относительно
биссектрисы угла
. А во втором решении замечено, что
— середина стороны
Тогда оказывается, что точка лежит на симедиане треугольника
. А сама задача тесно связана со следующим фактом:
окружность, проходящая через концы одной диагонали гармонического четырёхугольника и центр описанной около него
окружности, делит другую его диагональ пополам. Вы могли встретить его в такой задаче: пусть
— центр описанной
около треугольника
окружности,
— середина стороны
описанные около треугольников
и
окружности вторично пересекаются в точке
Тогда прямые
и
симметричны относительно биссектрисы угла
Ошибка.
Попробуйте повторить позже
В треугольнике с отношением сторон
биссектриса угла
пересекает сторону
в точке
Найдите длину
отрезка
если длина вектора
равна
Источники:
Подсказка 1
Давайте пробовать постепенно раскручивать задачу, пользуясь всеми условиями. Нам дана биссектриса треугольника. Какие тогда соотношения можно записать?
Подсказка 2
Верно, можно записать равенство отношений отрезков и сторон, тем более одно из них нам дано. Так же нам дали какую-то странную сумму векторов... Давайте тогда попробуем выразить AL через вектора, может эта сумма там и появится. Как это можно сделать?
Подсказка 3
Ага, можно для начала выразить AL через сумму двух векторов по правилу треугольника. Видим, что фигурируют неизвестные нам вектора, и в данной по условию сумме они не участвуют. Тогда попробуем заменить один из векторов по полученному равенству в 1 подсказке, а далее ещё раз воспользоваться правилом треугольника.
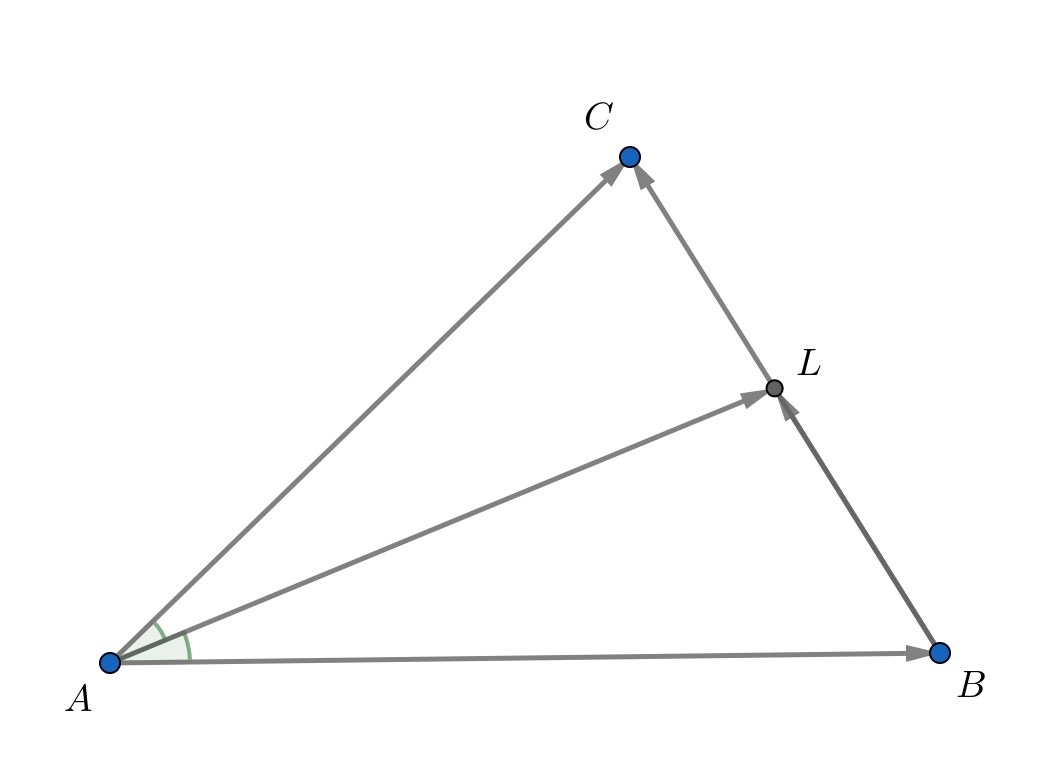
Поскольку по свойству биссектрисы то
тогда
Отсюда
Ошибка.
Попробуйте повторить позже
В равнобедренной трапеции с основаниями
и
боковая сторона равна 20 см, угол
равен
Пусть
— центр окружности, описанной вокруг
. Оказалось, что прямые
и
перпендикулярны. Найдите длину основания
трапеции.
Источники:
Пусть — середина
Тогда
и
Значит,
и
лежат на одной прямой и
— серединный
перпендикуляр к
Значит,
и если
то

Из вписанности следует, что
и значит,
и Тогда
Замечание.
можно посчитать из уравнения
и знания, что
Ошибка.
Попробуйте повторить позже
Основания и
трапеции
равны 65 и 31 соответственно, а её диагонали взаимно перпендикулярны. Найдите скалярное
произведение векторов
и
Источники:
Подсказка 1
Перед нами трапеция, у которой мы знаем соотношение оснований, а посчитать нам хочется модули векторов- значит, попробуем посчитать всевозможные отрезки на чертеже!
Подсказка 2
Нам известно, как выглядит скалярное произведение векторов, которые мы можем выразить как сумму векторов, выраженных через друг друга. Теперь нужно его записать и использовать угол!
Подсказка 3
Нужное скалярное произведение есть 31/65 от суммы квадратов длин векторов AO и BO. А как учесть угол?)
Пусть - точка пересечения диагоналей
и
. Из подобия треугольников
и
следует, что
, а
. Обозначим вектор
через
, а вектор
через
. Тогда, из условия следует, что
и
![]()
Откуда
где предпоследнее равенство следует из того, что треугольник - прямоугольный.
Ошибка.
Попробуйте повторить позже
Дан выпуклый пятиугольник . Точки
и
середины сторон
и
соответственно, точки
и
—
середины
и
соответственно. Найдите длину отрезка
, если
.
Источники:
Подсказка 1!
Попробуем отрезок MQ выразить двумя разными способами, чтобы приравнять и вычислить HK. Для этого в вычислениях должен встречаться HK. Попробуйте записать MQ двумя различными способами
Подсказка 2!
Например, как две покрывающие его ломаные, например, MH + HK + KQ. И вторая ломаная, MB + BC + CD + DQ
Подсказка 3!
То есть теперь попробуем выразить все отрезки через AB, BC, CD, DE и отношения с ними, а Hk оставить нетронутым, чтобы выразить!
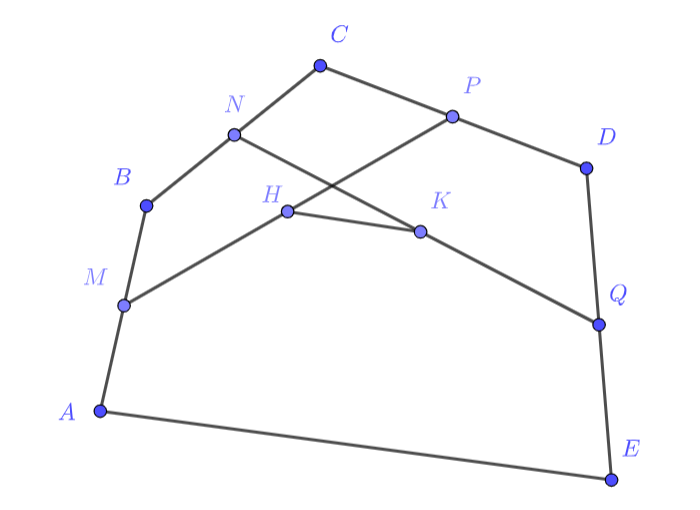
Опустим везде обозначения векторов, поскольку больше ничего использовать не будем. Выразим двумя способами
Распишем более подробно первое равенство
Приравнивая и
, имеем
Ошибка.
Попробуйте повторить позже
Диагонали трапеции взаимно перпендикулярны, а боковые стороны образуют угол . Основания имеют длины
и
Найдите высоту
трапеции.
Подсказка 1
Нам нужно найти высоту трапеции. Давайте подумаем, как это будет проще всего сделать. Например, если обозначить угол между основанием и диагональю за α, то высота это BD * sinα. А как можно выразить диагональ, зная угол?
Подсказка 2
Ага, так как диагонали перпендикулярны, то образуются прямоугольные треугольники, и все отрезки диагоналей легко выражаются через α. Выходит, что высота это 8cos(α)sin(α). Теперь наша задача найти угол α. Какое дополнительное построение удобно сделать в данном случае, зная угол между боковыми сторонами?
Подсказка 3
Верно, давайте достроим нашу трапецию до параллелограмма. Получается треугольник с углом при вершине в 30 градусов. Заметим, что все его стороны мы можем выразить из прямоугольных треугольников внутри трапеции, используя только угол α. Какой добивающей теоремой теперь можно воспользоваться?
Подсказка 4
Да, воспользуемся теоремой косинусов, потому что все стороны и угол в 30 градусов нам известны. Осталось только аккуратно найти α и выразить высоту. Победа!

Пусть эта трапеция . При этом
, а также
.
Построим , тогда
,
. Кроме того, из
получаем
. Введём также
. Используем прямой угол между диагоналями
. Отсюда
,
(
). Теперь мы готовы
написать теорему косинусов для
Оба значения подходят, поскольку обозначения в условии симметричны. Не умаляя общности, , откуда
. Осталось заметить, что высота трапеции равна
Ошибка.
Попробуйте повторить позже
В выпуклом четырёхугольнике прямые
и
перпендикулярны, а длина отрезка, соединяющего середины диагоналей
и
, равна
. Найдите длину отрезка, соединяющего середины сторон
и
.
Источники:
Подсказка 1
Пусть K,L,M,N-середины AB,AC,CD,BD. Тогда, к примеру в треугольнике ABC у нас есть две середины сторон. На проведение какого(каких?) доп.построения это может намекать?
Подсказка 2
Отлично, мы провели 4 средние линии. Но ведь средняя линия параллельна стороне треугольника! Тогда что можно сказать про ч-угольник KLMN , используя условие, что AD перпендикулярно BC?
Подсказка 3
Да, то что KLMN-прямоугольник. Дело остается за малым, ведь осталось лишь применить одно свойство прямоугольника, чтобы найти KM
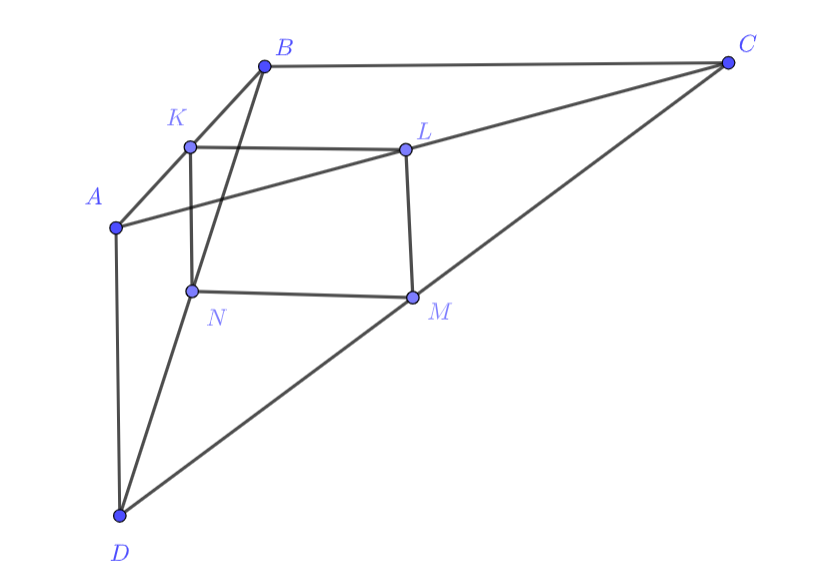
Первое решение.
Пусть — середины
соответственно. Заметим, что
, как средние линии в
. Аналогично
. Отсюда
— параллелограмм, в котором
в силу
, то
есть это прямоугольник, в котором диагонали равны. Осталось заметить, что его диагоналями и будут два отрезка из
условия.
Второе решение.
Пусть — середины
соответственно. Тогда, во-первых,
а во-вторых,
По условию дано
и
а найти надо
так что
Ошибка.
Попробуйте повторить позже
На плоскости задана точка . Рассматриваются различные равносторонние треугольники
, такие что
Какое
максимальное значение может принимать длина отрезка
Источники:
Счётный способ, подсказка 1
Заметим, что если зафиксировать треугольник PAB, то картинка определяется единственным образом. Как его зафиксировать?
Счётный способ, подсказка 2
Конечно, можно ввести лишь три его стороны, но лучше ввести еще и два угла, чтобы счет проходил легче(а с помощью теорем синусов или косинусов, мы всегда сможем связать углы со сторонами при желании).
Счётный способ, подсказка 3
Выразите сторону AB по теореме косинусов и угол PBA через стороны треугольника PAB и угол APB. Выразили? Кажется, все готово, чтобы считать PC.
Счётный способ, подсказка 4
Попробуйте привести выражение PC к такому виду, чтобы только одно слагаемое было переменным, а все остальное являлось константой.
Геометрический способ, подсказка 1
На картинке есть угол 60 градусов и два равных отрезка исходящих из него(AB и AC). Это очень сильно намекает на поворот в этой точке.
Геометрический способ, подсказка 2
Да, нужно сделать поворот на 60 градусов, переводящий точку B в точку C. Это удобно, так как точка P переедет в точку P’,при этом APP’-равносторонний и треугольники AP’C и APB равны. Какой вывод о длине PC можно сделать?
Геометрический способ, подсказка 3
Да, по неравенству треугольника PC<=5. Осталось лишь привести пример, но как? Попробуйте делать те же действия, как вы получили оценку, но в обратном порядке, не забывая о том, когда эта оценка достигается(расположение точек P,P’,C)
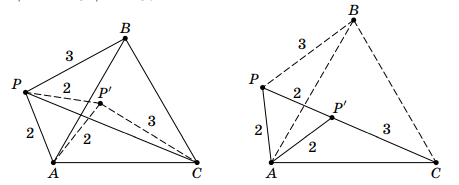
Первое решение.
Докажем, что длина не больше . Для этого рассмотрим поворот с центром в точке
на
таким образом, что
переходит в
.
Точка
переходит в
, а поскольку
и
, то
, откуда
по
неравенству треугольника.
Для построения примера сначала построим правильный , затем на продолжении
отметим
. Наконец, построим
правильный треугольник
на отрезке
. Остаётся показать, что выполнено
, но для этого достаточно рассмотреть поворот
на
в обратную сторону
, тогда отрезок
перейдёт в
.
Второе решение.
Просто посчитаем. Пусть ,
. Тогда из треугольника
из теоремы косинусов
следует
Теперь из треугольника по теореме косинусов



