Стереометрия на Физтехе

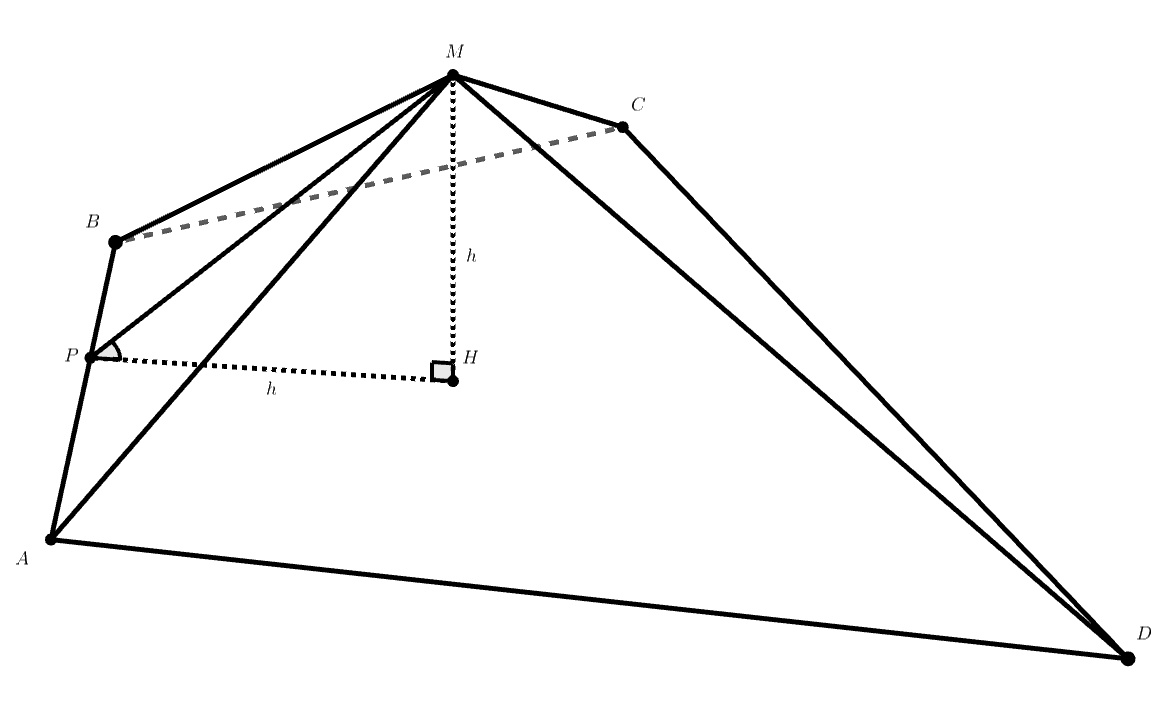
Пусть — высота пирамиды, — проекция на прямую . Тогда — прямоугольный треугольник с углом , откуда . Аналогично доказывается, что точка удалена от каждой из прямых на расстояние (иначе говоря, окружность радиуса с центром касается прямых .

Треугольники и равны по трем сторонам, поэтому четырёхугольник симметричен относительно диагонали . Его площадь равна , поэтому . Равенство достигается, когда , поэтому .

Точка лежит на внутренней или внешней биссектрисе каждого из углов четырехугольника является внутренней биссектрисой углов и . Внешние биссектрисы углов и параллельны, поэтому обязана лежать на .

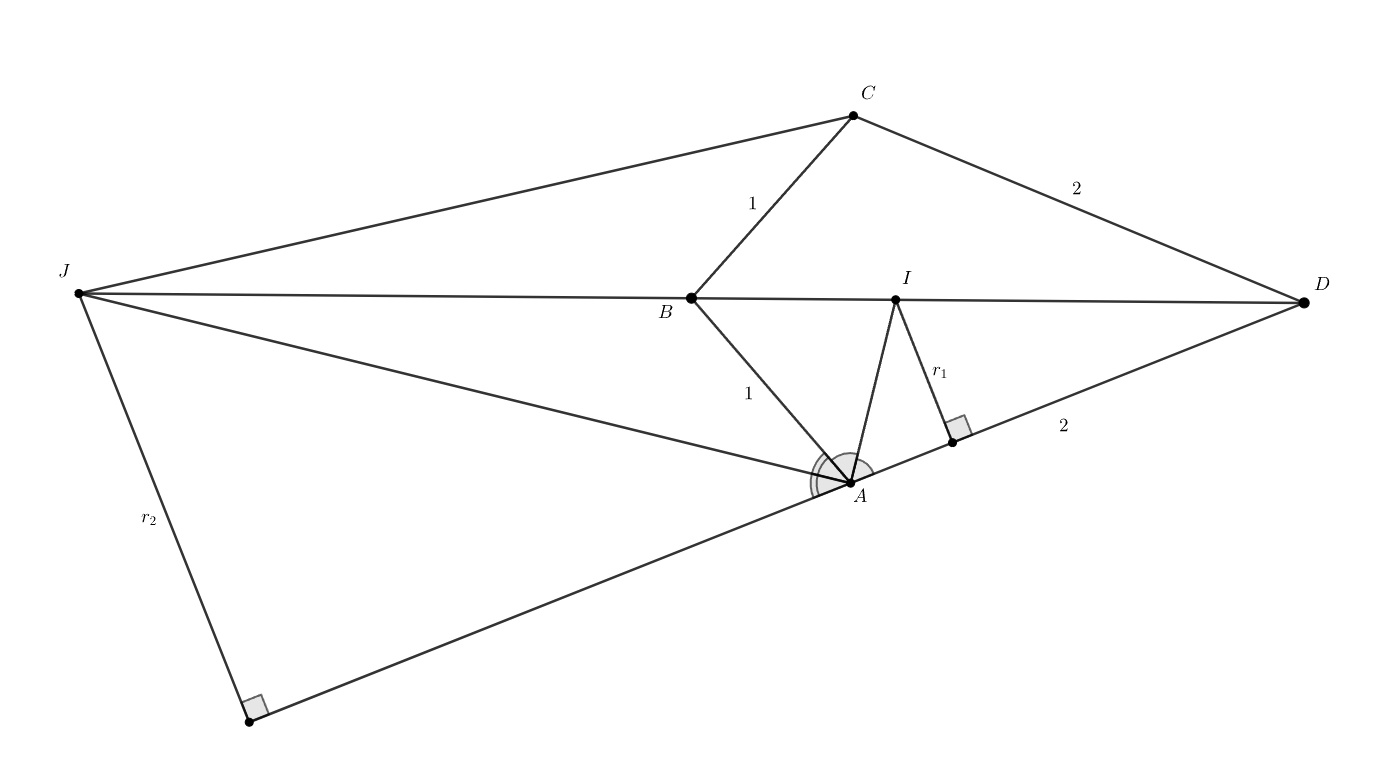
Обозначим через и точки пересечения внутренней и внешней биссектрис угла с прямой . Тогда — центр вписанной окружности четырёхугольника (пусть ее радиус равен ); центр окружности, касающейся продолжений сторон четырехугольника (вневписанной окружности, пусть ее радиус равен ). Площадь четырёхугольника, в который вписана окружность может быть задана формулой

откуда . Также

откуда .

Пирамида удовлетворяет условию задачи тогда и только тогда, когда (1) высота проходит через центр вписанной в основание окружности (т.е. ) и при этом её длина равна или (2) высота проходит через центр вневписанной окружности (т.е. ) и .

a) При первый случай невозможен ( ). Поэтому остаётся второй случай, и тогда . Объём равен .

б) Объём в первом и во втором случае равен

Наибольший объём