Стереометрия на Физтехе
Ошибка.
Попробуйте повторить позже
Сфера с диаметром 
пересекает рёбра 
и 
соответственно в точках 
и 
отличных от вершин призмы. Отрезки 
и 
пересекаются в точке 
и при этом 
.
.
Найдите объём призмы.
Пункт а, подсказка 1
Что можно сказать о точках T₁ и L₁?
Пункт а, подсказка 2
Они лежат на окружности с диаметром A₁B₁.
Пункт а, подсказка 3
Отметьте прямые углы.
Пункт а, подсказка 4
А чем является прямая B₁T₁?
Пункт а, подсказка 5
Это проекция BT₁.
Пункт b, подсказка 1
Что следует из пересечения прямых BT₁ и AL₁?
Пункт b, подсказка 2
Это значит, что их точки лежат в одной плоскости.
Пункт b, подсказка 3
Как расположены прямые AB и T₁L₁?
Пункт b, подсказка 4
Они не пересекаются и лежат в одной плоскости, следовательно, параллельны.
Пункт b, подсказка 5
Рассмотрите четырехугольник A₁T₁L₁B₁.
Пункт b, подсказка 6
Это трапеция. Вспомните про сферу.
Пункт b, подсказка 7
Оказывается, что трапеция вписана в окружность, значит, она равнобедренная!
Пункт b, подсказка 8
А какие треугольники есть на картинке? Найдутся ли среди них равные/подобные?
Пункт с, подсказка 1
Попробуйте посчитать площадь верхнего основания.
Пункт с, подсказка 2
Например, можно воспользоваться высотой B₁T₁.
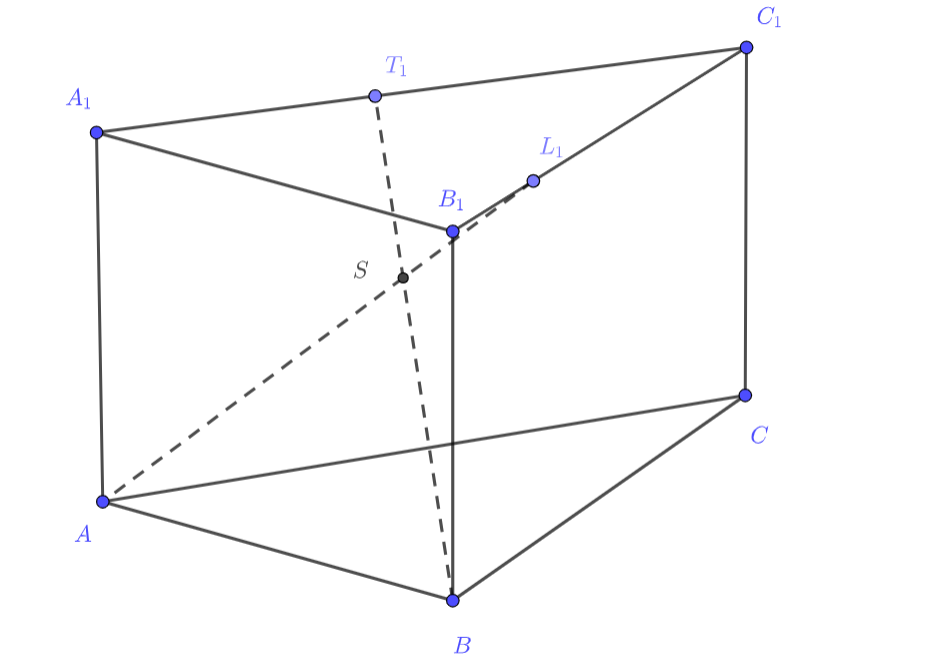
(a) Точки 
и 
лежат на окружности с диаметром 
значит, 
(т.е. 
и 
высоты
треугольника 
Прямая 
— это проекция прямой 
на плоскость основания, при этом 
Тогда по теореме
о трёх перпендикулярах 
т.e. 
(b) Поскольку прямые 
и 
пересекаются, то все четыре точки 
и 
лежат в одной плоскости (назовём
её 
). Значит, прямые 
и 
лежат в одной плоскости 
а так как они не пересекаются (поскольку лежат в
параллельных друг другу основаниях призмы), то 
Значит, 
Трапеция 
вписана в окружность,
следовательно, она равнобокая, тогда углы при её основании 
равны, и поэтому треугольник 
равнобедренный
Треугольники 
и 
подобны по двум углам. Из равенства треугольников 
и 
следует,
что 
поэтому оба треугольника 
и 
равнобедренные с основаниями 
и 
соответственно. Значит, 
откуда
(c) Если 
то 
; 
. Значит, площадь
основания призмы равна 
объём призмы равен 
.
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
