Параметры на Физтехе
Ошибка.
Попробуйте повторить позже
Найдите площадь фигуры, состоящей из всех точек с координатами , удовлетворяющими системе
Подсказка 1
Давайте разберёмся с первым неравенством. Видно, что без модуля оно станет совсем простым. Поэтому логичным решением будет рассмотреть случаи раскрытия модуля.
Подсказка 2
Итак, скорее всего вы поняли, что первое неравенство задаёт первую координатную четверть. Если нет, то обязательно разберитесь. Со вторым всё просто, там проблем возникать не должно. А что с третьим? С ходу непонятно, а если преобразовать?
Подсказка 3
В третьем неравенстве присутствуют переменные в первой степени и во второй. Обычно такие выражения легко преобразовываются в суммы квадратов. А что задают уравнения, в которых есть суммы квадратов?
Подсказка 4
Верно, окружность! Но тут стоит подумать насчёт взаимного расположения окружности и прямой из второго неравенства.
Первое неравенство при сводится к
а при
к
Поэтому множество точек, удовлетворяющих этому
неравенству, есть объединение двух множеств: в первом лежат все точки выше прямой
с неотрицательными абсциссами (включая
точки на прямой), а во втором лежат все точки ниже этой прямой (не включая точки на ней) с неотрицательными ординатами. Объединение
этих множеств есть первая координатная четверть (
).
Второе неравенство определяет полуплоскость, находящуюся ниже прямой (включая точки на прямой).
Первые два неравенства вместе определяют прямоугольный треугольник с вершинами:
Наконец, третье неравенство может быть записано в виде:
Оно задаёт внешность окружности с центром и радиусом
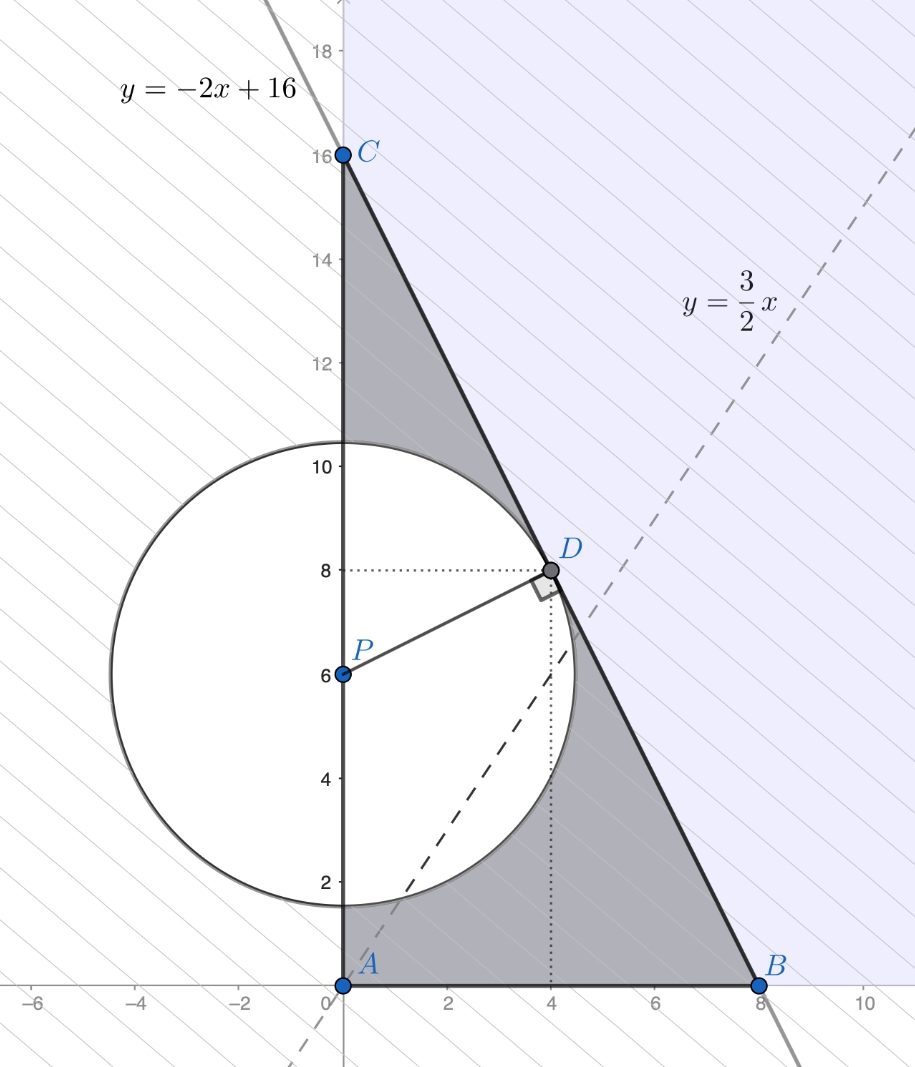
Поскольку система уравнений
имеет ровно одно решение окружность касается гипотенузы треугольника. Поэтому, внутри треугольника
оказывается
половина круга. Искомая площадь равна площади треугольника без половины площади круга:
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




