Параметры на Физтехе

Второе неравенство равносильно системе неравенств

Значит, исходная система равносильна следующим:

Множества точек, задаваемых этими неравенствами на плоскости и при этом выступают в роли параметров), - это круги радиуса с центрами соответственно. Условие задачи означает, что полученная система должна иметь решение относительно , то есть все три круга должны иметь по крайней мере одну общую точку.

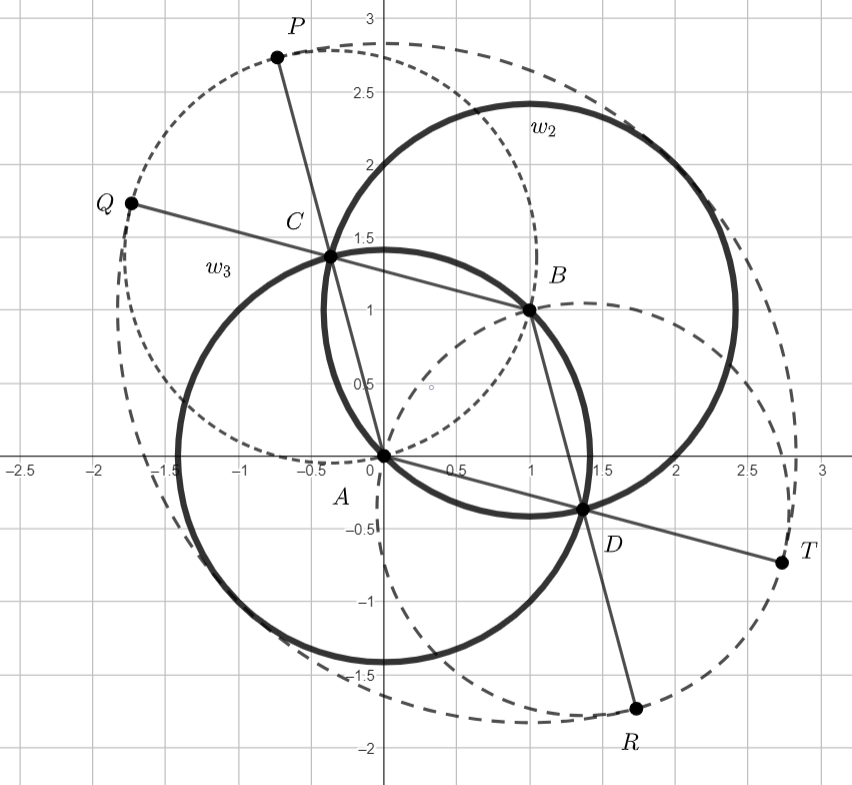
Пусть окружности, ограничивающие и , пересекаются в точках и (тогда треугольники и - равносторонние). Пересечение кругов и есть фигура , представляющая собой совокупность двух меньших сегментов этих кругов, ограниченных хордой . Тогда фигура состоит из всевозможных точек , находящихся на расстоянии не более от фигуры . (Это совокупность всех кругов радиуса , центры которых принадлежат фигуре .)

Пусть точки и симметричны точкам и (соответственно) относительно точки ; точки и симметричны точкам и (соответственно) относительно точки .

А само множество есть объединение следующих четырёх секторов (центральный угол всех секторов меньше ):

• сектор круга с центром в точке и радиуса
• сектор круга с центром в точке и радиуса
• сектор круга с центром в точке и радиуса
• сектор круга с центром в точке и радиуса

Заметим, что первые два сектора пересекаются по ромбу , и никаких других пересечений между секторами нет. При этом первые два сектора равны между собой, и последние два сектора также равны между собой. Таким образом, площадь фигуры равна

Изображено множество точек (в плоскости (𝑎; 𝑏), удовлетворяющих второму неравенству системы – 2 балла; указано (или изображено, описано) множество решений первого неравенства – баллы не добавляются; верно описан способ построения фигуры 𝑀 (например, совокупность кругов заданного радиуса, центры которых лежат в некотром множестве), но сама она построена неверно – 1 балл; изображена фигура 𝑀 – 3 балла; найдена её площадь – 2 балла. Если фигура 𝑀 изображена неверно, нахождение площади не оценивается, и за задачу ставится не более 3 баллов. Если фигура 𝑀 представляет собой пересечение двух кругов с центрами 𝐴 и 𝐵 радиусов 2𝐴𝐵, за задачу ставится 3 балла (при этом не играет роли, найдена ли площадь)