Параметры на Физтехе

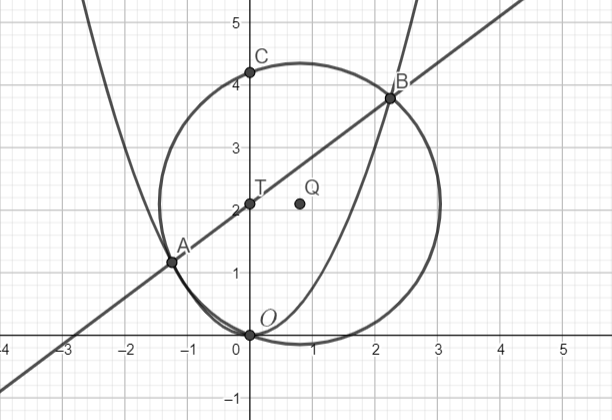
Рассмотрим сначала . Обозначим начало координат через , центр окружности через (так как он лежит на прямой , его ордината равна ; точки пересечения прямой с параболой через и . Пусть также — точка пересечения данной прямой с осью ординат, — точка пересечения окружности с осью ординат, отличная от .

Треугольник равнобедренный как радиусы), — его высота, следовательно, также и медиана, , поэтому точка имеет координаты . Опустим из точки перпендикуляр на ось ординат. Тогда есть угол наклона прямой, его тангенс равен . Отсюда . Аналогично находим, что .

и — две хорды данной окружности. По теореме о пересекающихся хордах , т.е. . Абсциссы и точек пересечения прямой и параболы определяются уравнением . По теореме Виета . Значит, , откуда .

Значение не подходит, так как при этом заданная прямая принимает вид , т.е. проходит через начало координат.

При (естественно, мы рассматриваем только те , при которых прямая и парабола имеют две точки пересечения) оба числа и положительны. Точка является серединой отрезка OC (сохраняем все обозначения первого случая). Тогда с одной стороны выходит, что точка — середина хорды , т.е. лежит внутри окружности. С другой стороны, точки и лежат на окружности, поэтому является хордой этой окружности, а точка лежит на продолжении хорды , т.е. вне окружности. Получаем противоречие, и этот случай невозможен.