Системы на Физтехе
Ошибка.
Попробуйте повторить позже
На координатной плоскости изображена фигура 
, состоящая из всех точек, координаты ( 
) которых удовлетворяют системе
неравенств
Найдите максимальное значение 
периметра (длины границы) фигуры 
и укажите все значения 
, при которых оно
достигается.
Источники:
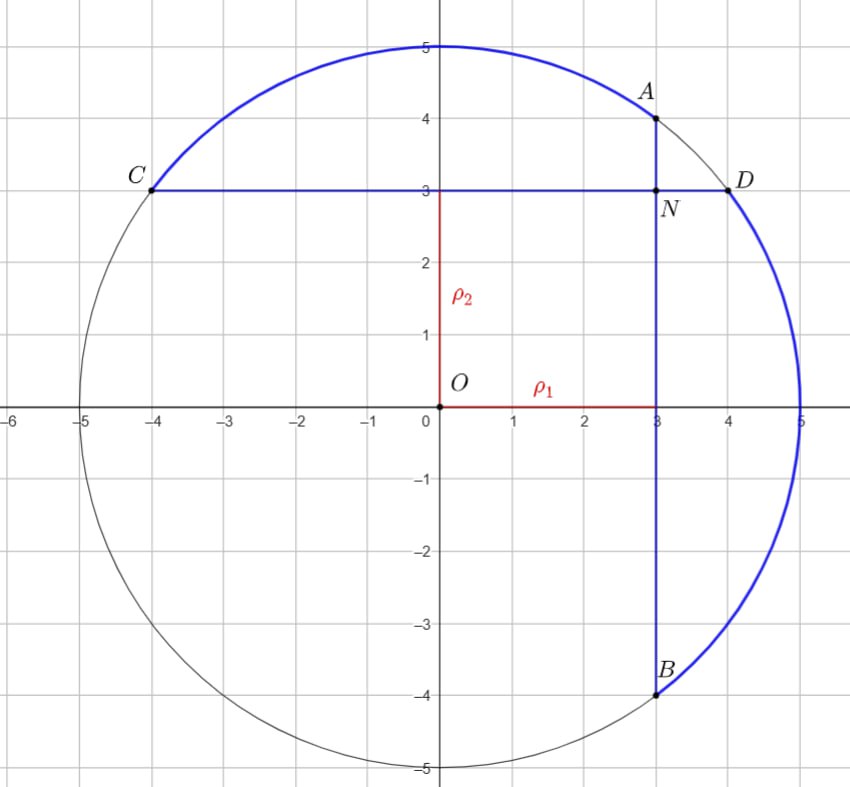
— это две части круга 
с центром в точке 
и радиуса 
, отсекаемые хордами 
и 
, лежащими на прямых с
уравнениями 
и 
соответственно. Хорды пересекаются в точке 
, которая принадлежит
, так как 
. Эта точка 
является единственной общей точкой двух частей
.
Периметр 
равен 
, где 
— сумма длин дуг 
и 
— сумма длин хорд 
и 
. Угол между 
и 
равен 
, поэтому
Расстояния от точки 
до 
и 
равны 
и 
соответственно, поэтому, используя неравенство
о среднем квадратическом и среднем арифметическом, получаем
Равенство достигается при
Тогда 
, а 
.
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
