Планиметрия на устном туре Турнира Городов
Ошибка.
Попробуйте повторить позже
На высотах 
остроугольного неравностороннего треугольника 
отметили соответственно точки 
так, что
где 
— радиус описанной окружности треугольника 
Докажите, что центр описанной окружности
треугольника 
совпадает с центром вписанной окружности треугольника 
Источники:
Подсказка 1
Рассмотрите симметрию относительно биссектрис: как связаны точки А₁, B₁, C₁ с центром описанной окружности О? Обратите внимание на равенство расстояний AA₁= BB₁= CC₁= R. Намёк: Проверьте, что О симметричен А относительно биссектрисы угла А)
Подсказка 2
Докажите, что IO = IA₁= IB₁= IC₁, где I — центр вписанной окружности. Какое свойство объединяет все точки, равноудалённые от I?
Подсказка 3
Почему А₁ и О относительно биссектрисы AI? Используйте равенство АA = R = AO и свойства высот. Точка А, лежит на высоте, а О — на серединном перпендикуляре. Как биссектриса связывает эти объекты?
Пусть 
— центр описанной окружности треугольника 
а 
— центр вписанной окружности данного треугольника.
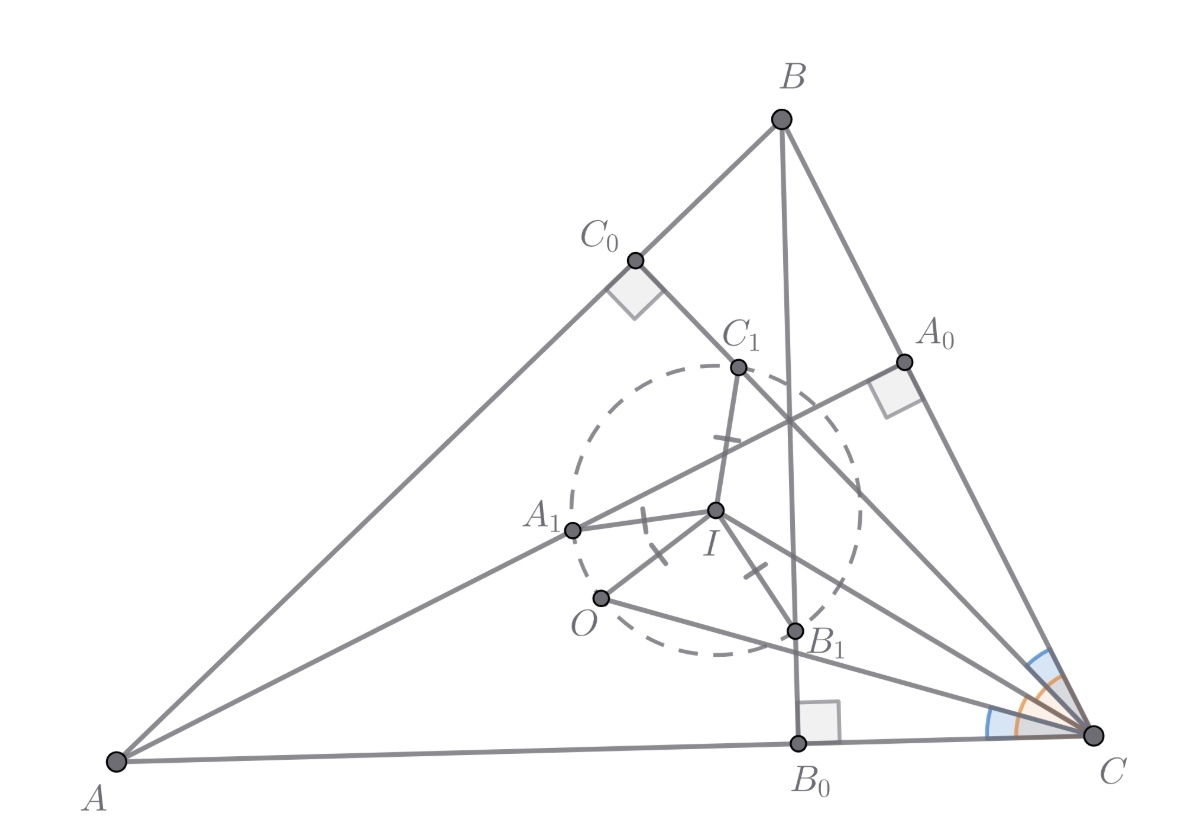
Заметим, что 
Тогда из равенства углов и того, что 
по условию, точки 
и 
симметричны
относительно биссектрисы 
Следовательно, 
Аналогичными рассуждениями получаем, что 
Из равенств
следует, что 
и есть центр описанной окружности треугольника 
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
