Планиметрия на устном туре Турнира Городов
Ошибка.
Попробуйте повторить позже
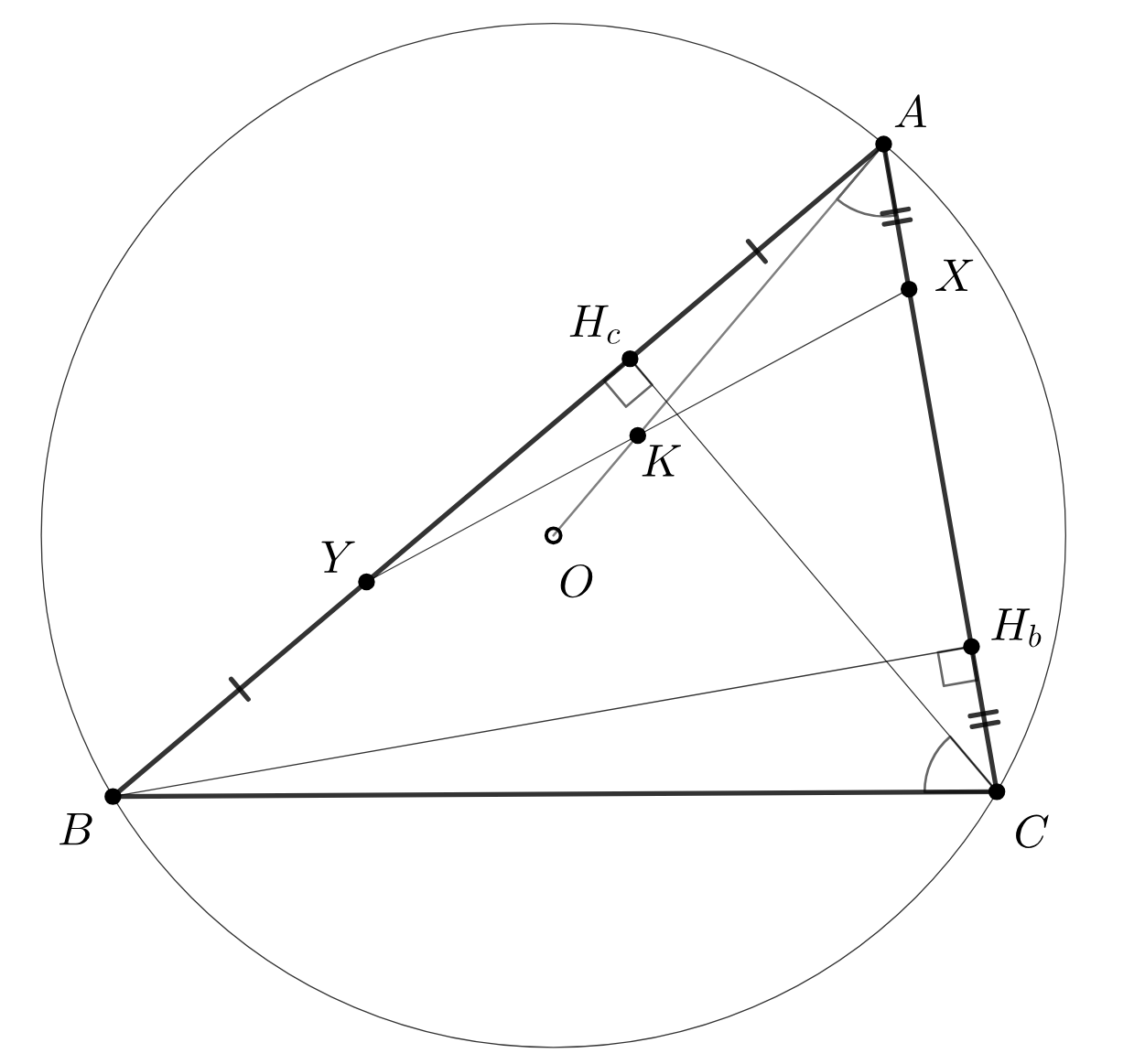
В остроугольном неравнобедренном треугольнике с центром описанной окружности
проведены высоты
и
Точки
и
симметричны точкам
и
относительно середин сторон
и
соответственно. Докажите, что прямая
делит
отрезок
пополам.
Источники:
Подсказка 1:
Пусть AO пересекает XY в точке K. Нас просят доказать равенство XK = KY или же отношение XK/KY. На какие мысли это наталкивает?
Подсказка 2:
Существует теорема, которая очень хорошо дружит с отношениями отрезков, это теорема синусов. Подумайте, к каким треугольникам её можно здесь применить?
Подсказка 3:
Попробуйте написать теоремы синусов для треугольников AXK и AYK. Если поделить одно на другое, то получится выразить отношение XK/KY через нечто, которое должно быть равно 1.
Пусть – точка пересечения прямых
и
Выразим по теореме синусов в треугольниках и
отношение отрезков
и
Ясно, что и
Из прямоугольных треугольников
и
следует, что
Осталось лишь заметить, что и
поскольку
– направление на
центр описанной окружности. Получается, что
что и требовалось доказать.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




