Планиметрия на устном туре Турнира Городов

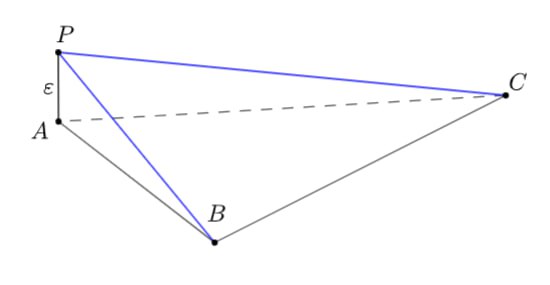
Докажем сначала, что неравносторонний треугольник под условие подходить не может. Предположим противное, пусть такой треугольник есть и в нём причём длины этих сторон различаются хотя бы на

Рассмотрим точку расположенную на перпендикуляре к плоскости проходящем через точку на расстоянии от Тогда

Можно выбрать настолько близко к вершине уменьшая чтобы и отличались соответственно от и меньше, чем на и чтобы было меньше Тогда стороны и будут различаться более чем на а длина стороны меньше — противоречие с неравенством треугольника.

Покажем теперь, что равносторонний треугольник удобен. Пусть Отметим на лучах точки так, чтобы выполнялись равенства:

Треугольники и подобны по углу и отношению двух сторон, откуда

Аналогично вычисляем длины остальных сторон. Получаем, что треугольник — искомый.