Тема ТурГор (Турнир Городов)

Планиметрия на устном туре Турнира Городов

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела тургор (турнир городов)

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#85508

Точки $P,Q$ лежат внутри окружности $ω$ . Серединный перпендикуляр к отрезку $PQ$ пересекает $ω$ в точках $A$ и $D$ . Окружность с центром $D$ , проходящая через $P$ и $Q$ , пересекает $ω$ в точках $B$ и $C$ . Отрезок $PQ$ лежит внутри треугольника $ABC$ . Докажите, что $∠ACP =∠BCQ$ .

Источники: Турнир городов - 2024, весенний тур, 11.2 (см. turgor.ru)

Подсказки к задаче

Подсказка 1

Про окружность ω пока толком ничего не известно, а вот окружность с центром в D даёт сразу 4 равных отрезка (равенство радиусов) на чертеже. Посмотрите, что из этого можно взять для окружности ω.

Подсказка 2

Так как BD=DC, то дуги ВD и DC в ω равны, значит, AD — биссектриса ∠BAC.

Подсказка 3

Пусть I — точка пересечения отрезка АD и дуги BPQC, тогда по теореме о трилистнике I — центр вписанной в ΔABC окружности. Что же можно взять из этого факта, если в задаче нам нужно доказать равенство углов?

Подсказка 4

Конечно! То, что CI — биссектриса ∠BСА. Для завершения доказательства не хватает равенства ∠PCI и ∠ICQ, но это совсем несложно получить, если Вы ещё не забыли, чем по условию является AD для отрезка PQ.

Показать доказательство

$PIC$

Первое решение.

Пусть $I$ — точка пересечения отрезка $AD$ и дуги $BPQC$ . Так как $DB = DC$ , то $AD$ — биссектриса угла $BAC$ и по теореме о трилистнике $I$ — центр вписанной в треугольник $ABC$ окружности. Следовательно, $CI$ — биссектриса угла $ACB$ . С другой стороны, так как $AD −$ серединный перпендикуляр к $P Q$ , то $PI = QI$ , то есть $CI$ — биссектриса угла $PCQ$ . Из этих двух утверждений следует утверждение задачи.

_________________________________________________________________________________________________________________________________________________________________________________

Второе решение.

Обозначим $∠ACQ =α,∠QCP = β,∠PCB = γ$ . Необходимо доказать, что $γ = α$ .

Заметим, что

α+ β+ γ = ∠ACB = ∠ADB = ∠BDP +∠PDA

Далее, $∠BDP = 2∠BCP = 2γ$ , как центральный и вписанный в окружность ( $DP Q$ ), а также $∠P DA = 12∠PDQ = 12 ⋅2∠PCQ = β$ , как центральный и вписанный в окружность ( $DPQ$ ). Тогда

α+ β+ γ = ∠BDP + ∠PDA = 2γ+β

γ =α

______________________________________________________________________________________________________________________________________________________

Замечание.

В условии задачи дано, что точки $P$ и $Q$ лежат не только внутри окружности $ω$ , но и внутри вписанного в неё треугольника $ABC$ . Последнее условие на самом деле излишне. Из остальных условий задачи следует, что точки $P$ и $Q$ изогонально сопряжены относительно треугольника $ABC$ . Но если обе изогональные точки лежат внутри описанной окружности, то они лежат и внутри треугольника, поскольку при изогональном сопряжении три сегмента, ограниченные сторонами треугольника и дугами описанной окружности, переходят в три угла, вертикальных углам треугольника

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#67558

Дан треугольник $ABC.$ Пусть $I$ — центр его вписанной окружности, $P$ — такая точка на стороне $AB,$ что угол $PIB$ прямой, $Q$ — точка, симметричная точке $I$ относительно вершины $A.$ Докажите, что точки $C,I,P,Q$ лежат на одной окружности.

Источники: Турнир городов - 2023, 11.4, авторы - И. Кухарчук, А.Юран

Подсказки к задаче

Подсказка 1

Условие на угол PIB выглядит немного странно...однако он входит в состав угла AIB (I - центр вписанной окружности, так еще нам и намекают число 90) Какой угол тогда хочется сразу посчитать?

Подсказка 2

Угол AIB на 90 больше половины угла ACB, а, значит, углы ACI и AIP равны. На картинке много биссектрис, которые могут помочь нам в поисках подобных треугольников. А еще хочется как-то пользоваться равенством отрезков QA и AI(мы этого еще не делали)

Подсказка 3

Треугольники CIA и IPA подобны по трем углам, а в них как раз присутствует отрезок IA, так что можем записать, что IC/IP = AC/AI = AC/AQ. Смотрим, какие же треугольники содержат отрезки IC, IP, AC, IQ (или хотя бы часть из них, чтобы дальше работать с подобием)?

Подсказка 4

Треугольники ICP и ACQ! Становится ясно: хотим равенства углов CIP и CAQ, чтобы доказать подобие треугольников с такими же названиями, чтобы доказать равенство углов IPC и AQC. Посчитать угол QAC как внешний к половине угла BAC несложно, а угол PIC есть сумма углов AIP и AIC. Осталось лишь воспользоваться знанием про углы с вершиной I из подсказки 2 ;)

Показать доказательство

$PIC$

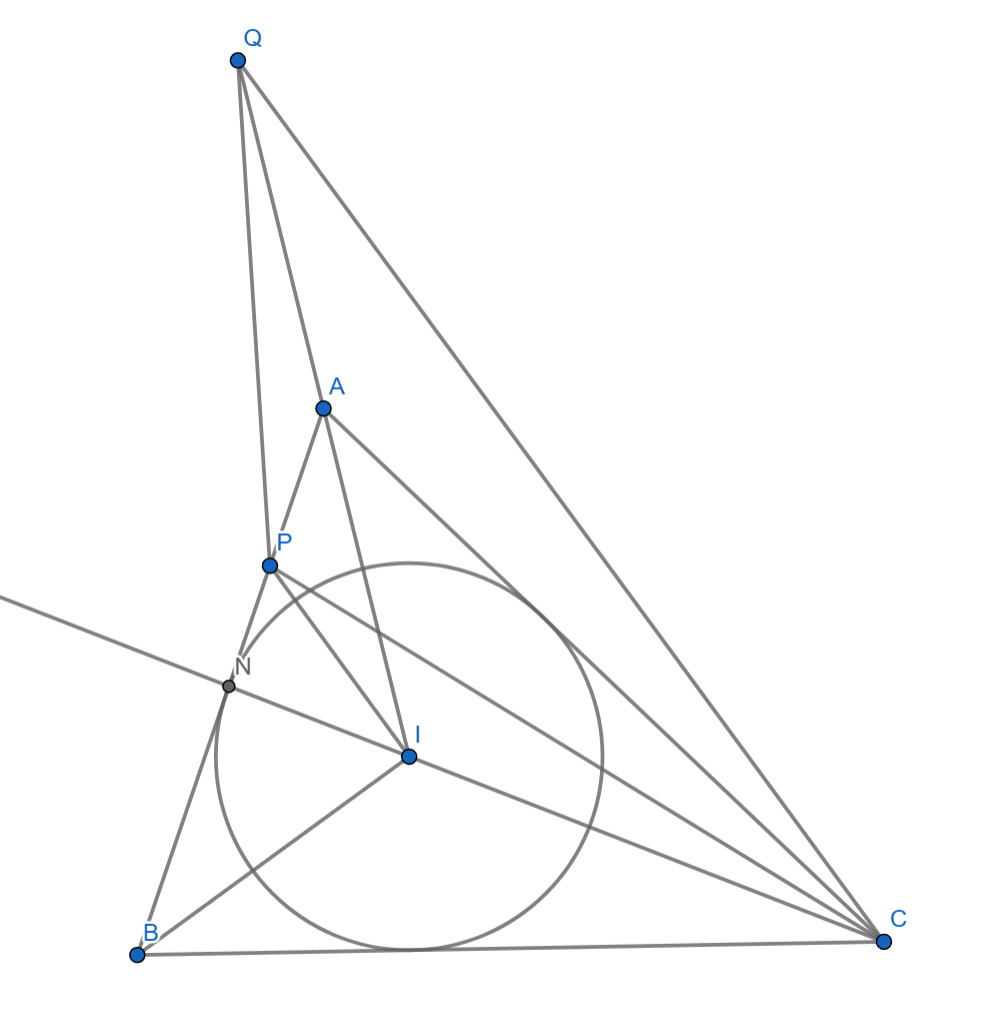
Пусть $CI$ пересекает $AB$ в точке $N.$ Угол $AIB$ тупой, а угол $NIB$ острый, значит $P$ лежит между $A$ и $N.$ Далее, т.к. $I$ — центр вписанной окружности треугольника, получаем

∠AIP = ∠AIB − 90∘ = 1∠ACB = ∠ACI 2

∠CAI = ∠IAP

Значит, треугольники $CAI$ и $IAP$ подобны. Учитывая это и равенство $QA = AI,$ имеем

-IC-= P-I= P-I AC AI QA

Кроме того,

( ) ∠AIP + ∠AIC = 1∠ACB + 90∘+ 1∠ABC = 180∘− 1∠CAB 2 2 2

Следовательно,

∘ 1 ∘ ∠PIC = 180 − 2∠CAB =180 − ∠CAI = ∠QAC

Тогда треугольники $QAC$ и $PIC$ подобны по углу и отношению прилежащих сторон, значит $∠IPC =∠AQC =∠IQC,$ и точки $C,I,P,Q$ лежат на одной окружности.

Замечание. После доказательства подобия треугольников $CAI$ и $IAP$ можно действовать по-другому. Выберем точку $R$ на продолжении отрезка $CA$ за точку $A$ так, что $AP =AR;$ тогда треугольники $IAP$ и $QAR$ равны ( $IA= QA,AP = AR,∠QAR = ∠CAI = ∠IAP$ ). Значит, $QRP I$ — равнобокая трапеция, и она вписана. С другой стороны, поскольку $∠CIQ = ∠CIA =∠CRQ,$ точки $C,I,R,Q$ лежат на одной окружности. Значит, все пять точек $C,I,P,Q,R$ лежат на окружности $(QRI).$

Ошибка.
Попробуйте повторить позже

Задача 3#75130

Дан неравнобедренный треугольник $ABC.$ Выберем произвольную окружность $ω,$ касающуюся описанной окружности треугольника $ABC$ внутренним образом в точке $B$ и не пересекающую прямую $AC.$ Отметим на $ω$ точки $P$ и $Q$ так, чтобы прямые $AP$ и $CQ$ касались $ω,$ а отрезки $AP$ и $CQ$ пересекались внутри треугольника $ABC.$ Докажите, что все полученные таким образом прямые $P Q$ проходят через одну фиксированную точку, не зависящую от выбора окружности $ω.$

Источники: Турнир городов - 2022, 11.5 (см. www.turgor.ru)

Показать доказательство

Пусть $R$ — точка пересечения касательных $AP$ и $CQ.$ Докажем, что все прямые $PQ$ проходят через точку $D$ — основание внешней биссектрисы угла $B$ треугольника $ABC$ (точка $D$ существует, так как треугольник неравнобедренный).

$PIC$

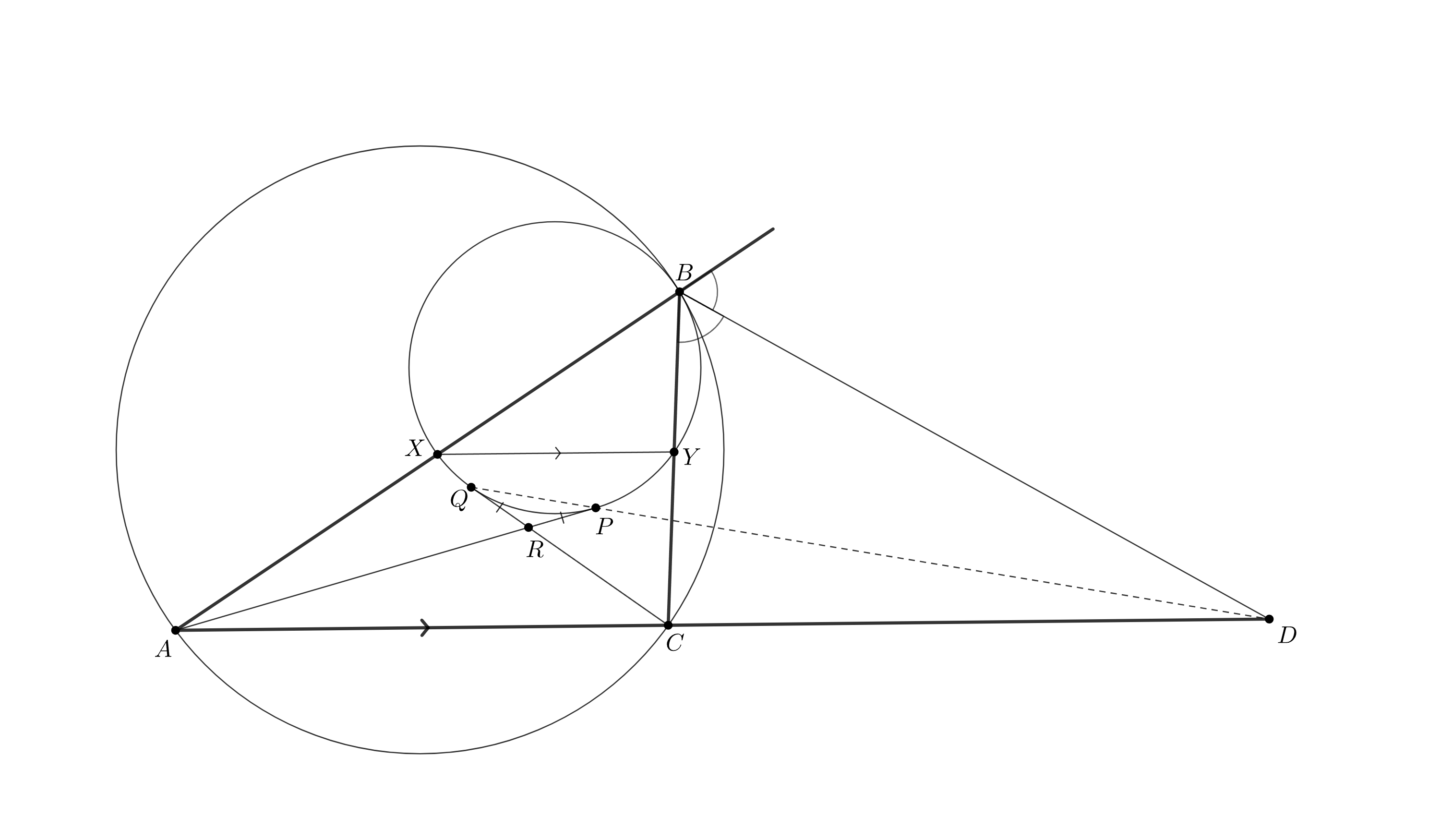
По теореме, обратной к теореме Менелая, для треугольника $ARC,$ достаточно проверить, что

AP-⋅ RQ-⋅ CD-= 1 PR QC DA

Поскольку $RQ$ и $PR$ равны как касательные, достаточно проверить равенство

AP- AD- QC = DC

Но по свойству внешней биссектрисы

AB AD BC-= DC-

Так что проверяем равенство

AP- AB- QC = BC

Пусть $AB$ и $BC$ пересекают окружность $ω$ в точках $X$ и $Y$ соответственно. Запишем степени точек $A$ и $C$ относительно окружности $ω :$

AX ⋅AB = AP 2, CY ⋅CB = CQ2

Осталось проверить равенство

AX CY AB-= CB-

Это равенство следует из того, что $ω$ касается описанной окружности треугольника $ABC$ в точке $B.$

Ошибка.
Попробуйте повторить позже

Задача 4#76582

Назовём расположенный в пространстве треугольник $ABC$ удобным, если для любой точки $P$ вне его плоскости из отрезков $PA,PB$ и $P C$ можно сложить треугольник. Какие углы может иметь удобный треугольник?

Подсказки к задаче

Подсказка 1

Если поразмыслить над этой задачей, порисовать какие-то треугольники и точки Р, можно понять, что если брать точку Р очень близко к одной из вершин (допустим, к А), выполнение неравенства треугольника для РА, РВ, РС сводится к тому, что АВ и АС не могут быть сильно отличны по длине.

Подсказка 2

Конечно, мысли из первой подсказки нужно формализовать. Тогда мы придем к тому, что если условие задачи выполнено, то треугольник АВС равносторонний. Теперь для равностороннего треугольника нужно доказать, что для любой точки P условие задачи выполнено.

Подсказка 3

Доказывать это можно по-разному. Один из способов (красивый) — явно построить треугольник со сторонами, равными PA, PB и РС, используя подобия.

Показать ответ и решение

Докажем сначала, что неравносторонний треугольник под условие подходить не может. Предположим противное, пусть такой треугольник $ABC$ есть и в нём $AB ⁄= AC,$ причём длины этих сторон различаются хотя бы на $d.$

Рассмотрим точку $P,$ расположенную на перпендикуляре к плоскости $ABC,$ проходящем через точку $A,$ на расстоянии $𝜀$ от $A.$ Тогда

∘ ------- ∘ ------- PB = AB2+ 𝜀2, PC = AC2 +𝜀2

Можно выбрать $P$ настолько близко к вершине $A,$ уменьшая $𝜀,$ чтобы $PB$ и $P C$ отличались соответственно от $AB$ и $AC$ меньше, чем на $d∕3,$ и чтобы $𝜀$ было меньше $d∕3.$ Тогда стороны $PB$ и $P C$ будут различаться более чем на $d∕3,$ а длина стороны $P A$ меньше $d∕3$ — противоречие с неравенством треугольника.

Покажем теперь, что равносторонний треугольник удобен. Пусть $AB = BC =CA.$ Отметим на лучах $PA,PB,P C$ точки $A1,B1,C1$ так, чтобы выполнялись равенства:

AB ⋅P A1 = PB ⋅PC

BC ⋅PB1 = PC ⋅PA

CA ⋅PC1 = PB ⋅PA

Треугольники $APB$ и $B1P A1$ подобны по углу и отношению двух сторон, откуда

AB-⋅P-A1 A1B1 = PB = PC

Аналогично вычисляем длины остальных сторон. Получаем, что треугольник $A1B1C1$ — искомый.

Ответ:

$60∘,60∘,60∘$

Ошибка.
Попробуйте повторить позже

Задача 5#92425

Точка $I$ — центр вписанной окружности треугольника $ABC$ , а $T$ — точка касания этой окружности со стороной $AC$ . Пусть $P$ и $Q$ — ортоцентры треугольников $BAI$ и $BCI$ соответственно. Докажите, что точки $T,P,Q$ лежат на одной прямой.

Источники: Тургор - 2021, 11.3, устный тур (см. turgor.ru)

Подсказки к задаче

Подсказка 1

Самый простой способ доказать, что точки Q, T, P лежат на одной прямой - это показать, что ∠QTC = ∠ATP. Однако простым счётом уголков к ∠QTC и ∠ATP не подобраться. Тогда можно попробовать доказать это через подобие треугольников ATP и QTC.

Подсказка 2

Воспользуемся тем, что P и Q — ортоцентры. Мы получаем, что AP ⊥ BE и QC ⊥ BE. Что тогда можно сказать про прямые AP и BE?

Подсказка 3

Верно! Они же параллельные, а значит, ∠PAT = ∠QCT. Отлично! Теперь для подобия осталось лишь показать, что AT/AP = CT/CQ. Но мы ещё никак не использовали, что T — точка касания. Отметьте две другие точки касания вписанной окружности с треугольником и попробуйте переносить отрезки.

Подсказка 4

Теперь мы получаем, что достаточно доказать, что AK/AP = CL/CQ (L - точка касания вписанной окружности с BC). Можно заметить, что это стороны △APK и △CQL. Что можно сказать про эти треугольники?

Показать доказательство

Первое решение.

Случай $AB =BC$ очевиден. Иначе основания $F$ и $E$ высот $AF$ и $CE$ лежат на биссектрисе $BI$ по разные стороны от $AC$ , прямые $AP$ и $CQ$ параллельны и $∠PAT = ∠FAT =∠ECT =∠QCT$ . Задача будет решена, если мы докажем подобие треугольников $TAP$ и $TCQ$ (тогда равные углы $CT Q$ и $ATP$ вертикальны и точки $P,Q,T$ лежат на одной прямой). Для этого достаточно проверить, что $AT ∕AP = CT∕CQ$ .

$PIC$

Пусть $K$ и $L$ — точки касания окружности со сторонами $AB$ и $BC$ соответственно. Тогда $AT = AK,CT = CL$ , и осталось доказать равенство $AK ∕AP = CL∕CQ$ . Оно следует из подобия треугольников $AP K$ и $CQL$ : они прямоугольные, а поскольку $BI$ — биссектриса угла $B$ , углы $BAP$ и $BCQ$ равны.

Второе решение.

Так как $AP$ содержит высоту треугольника $ABI$ , то $AP ⊥ BI$ . Пусть $K$ — точка касания $AB$ со вписанной окружностью, так что $K = PI∩ AB$ . Тогда

TA∕PA = KA∕PA = sin∠AP K = sin∠ABI = sin ∠B 2

Аналогично $CQ ⊥ BI$ , откуда $CQ ∥AP$ . И также $TC∕QC = sin∠B- 2$ , откуда $T A∕PA =TC ∕QC$ . Таким образом, $△T AP ∼ △TCQ$ . Значит, $∠AT P =∠CT Q$ , откуда и следует, что $T,P,Q$ на одной прямой.

Ошибка.
Попробуйте повторить позже

Задача 6#91019

В остроугольном треугольнике $ABC$ на высоте $BH$ выбрана произвольная точка $X.$ Точки $M$ и $N$ – середины сторон $AB$ и $BC$ соответственно. Перпендикуляр, опущенный из $M$ на $AX,$ пересекается с перпендикуляром, опущенным из $N$ на $CX,$ в точке $P.$ Докажите, что точка $P$ равноудалена от точек $A$ и $C.$

Показать доказательство

$PIC$

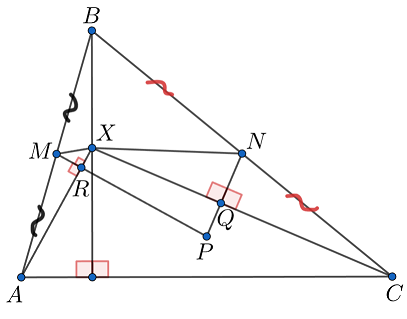
Обозначим через $R$ и $Q$ основания перпендикуляров, опущенных из $M$ и $N.$ Достаточно показать, что $CP 2+ XR2 =XQ2 + AR2,$ тогда по теореме Карно для треугольника $AXC$ точка $P$ будет лежать на серединном перпендикуляре к $AC,$ что равносильно требуемому. Выразим квадраты из равенства с помощью теоремы Пифагора для треугольников $AMR, MRX, XNP$ и $NP C$ :

(CN2 − NQ2 )+(MX2 − MR2 )= (XN2 − QN2)+ (AM2 − MR2 )

Приведём подобные:

CN2 +MX2 = XN2 +AM2

Домножим равенство на $4,$ запишем $2 4CN$ как $2 2 BC ,4AM$ как $2 AB ,$ а квадраты $MX$ и $XN$ распишем с помощью формулы медианы для треугольников $ABX$ и $CBX :$