Стереометрия на ММО

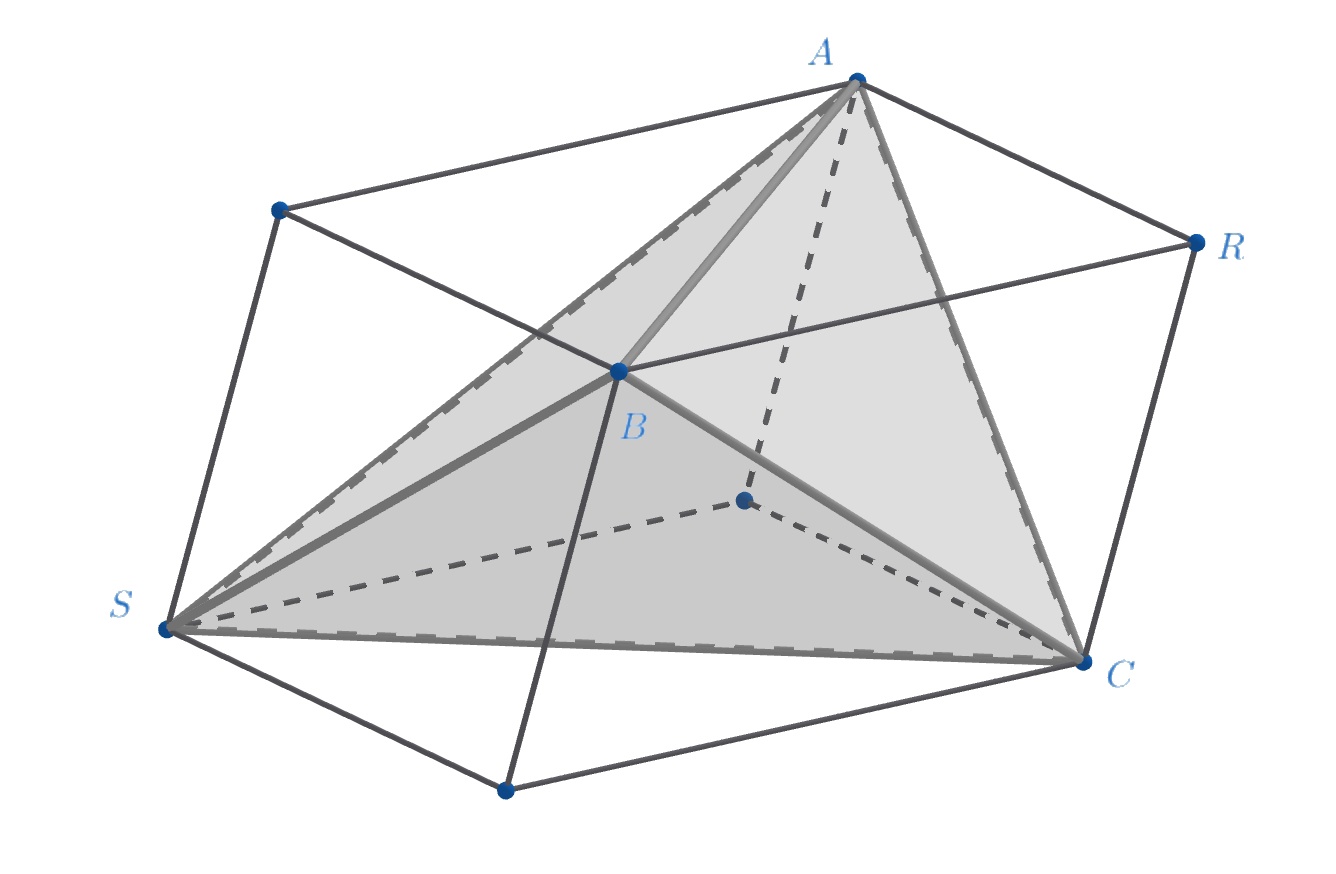
Решение 1. Пусть рёбра параллельны граням и соответственно. Проведём через плоскости, которые параллельны и соответственно. Получается параллелепипед, пять вершин которого совпадают с вершинами наших пирамид. Пусть — объём этого параллелепипеда. Тогда объём пирамиды равен как и объём трёх других пирамид, основаниями которых являются грани тетраэдра Поэтому объём пирамиды равен

то есть вдвое больше объёма пирамиды что и требовалось доказать.

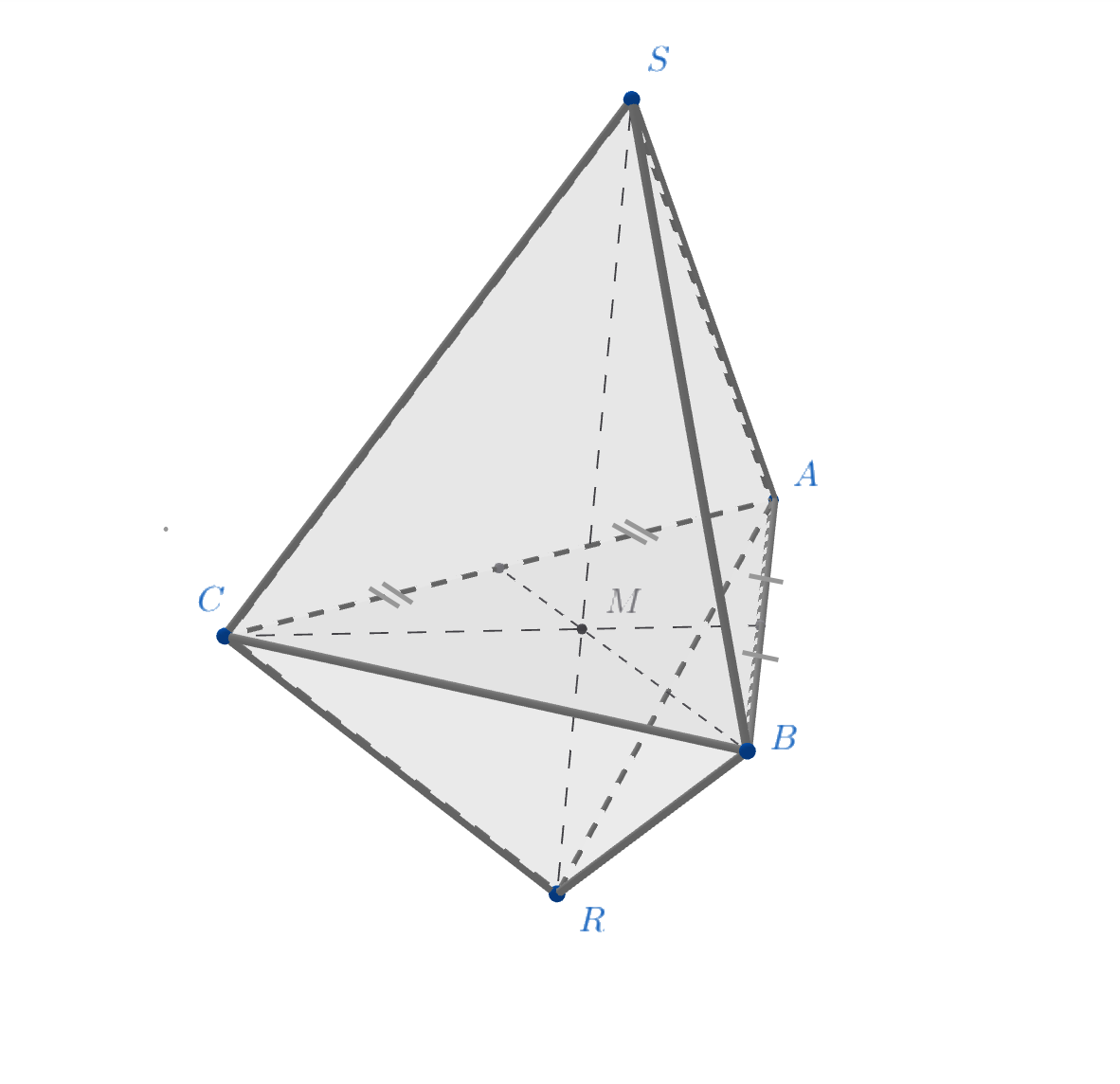
Решение 2. Пусть — точка пересечения медиан треугольника Пусть — плоскости, проходящие через точки параллельные плоскостям соответственно. Поскольку точка лежит в плоскости Аналогично, она лежит и в плоскостях и Пусть — образ точки при гомотетии с центром в точке и коэффициентом При этой гомотетии середина отрезка переходит в поэтому плоскость переходит в плоскость Значит, Аналогично, и

Плоскости имеют единственную общую точку, поэтому их образы при рассматриваемой гомотетии тоже имеют единственную общую точку. Таким образом, получаем, что По построению точки расстояние от неё до плоскости в два раза больше, чем расстояние от до этой плоскости, поэтому объём пирамиды (она же вдвое больше объёма пирамиды