Стереометрия на ММО

Первое решение. Покажем, что если у тетраэдра два скрещивающихся ребра перпендикулярны и имеют длины и то существует сечение тетраэдра, которое является квадратом со стороной

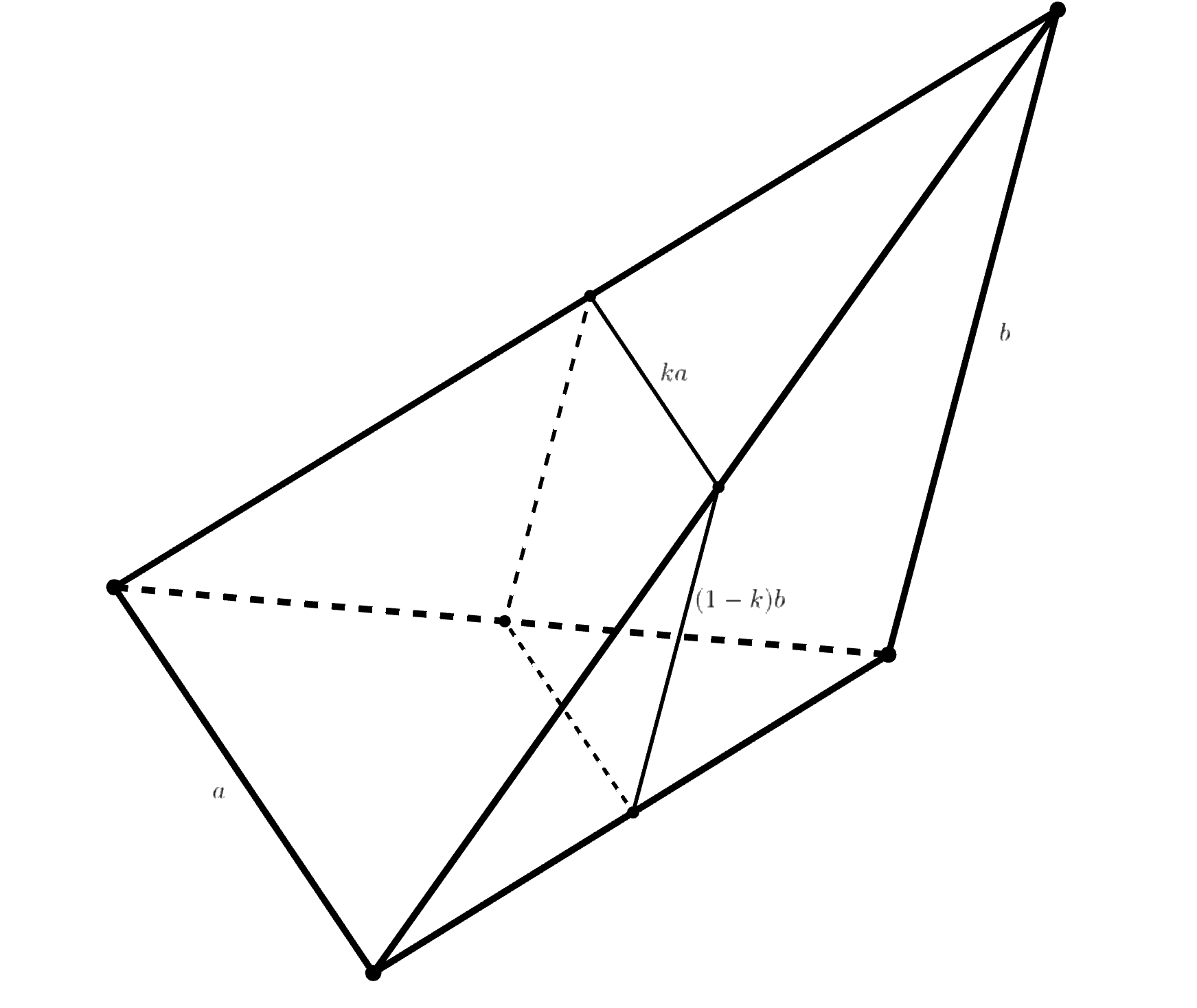
Разделим четыре остальных ребра тетраэдра в отношении считая от концов ребра длины (см. рис.). Соединив точки деления, получим сечение, которое является параллелограммом со сторонами длины и в силу подобия треугольников. На самом деле, это сечение является прямоугольником, поскольку стороны параллелограмма параллельны перпендикулярным рёбрам тетраэдра по обратной теореме Фалеса и, следовательно, тоже перпендикулярны. Осталось подобрать таким образом, чтобы стороны прямоугольника были равны, т. е. откуда При этом сторона получившегося квадрата будет равна

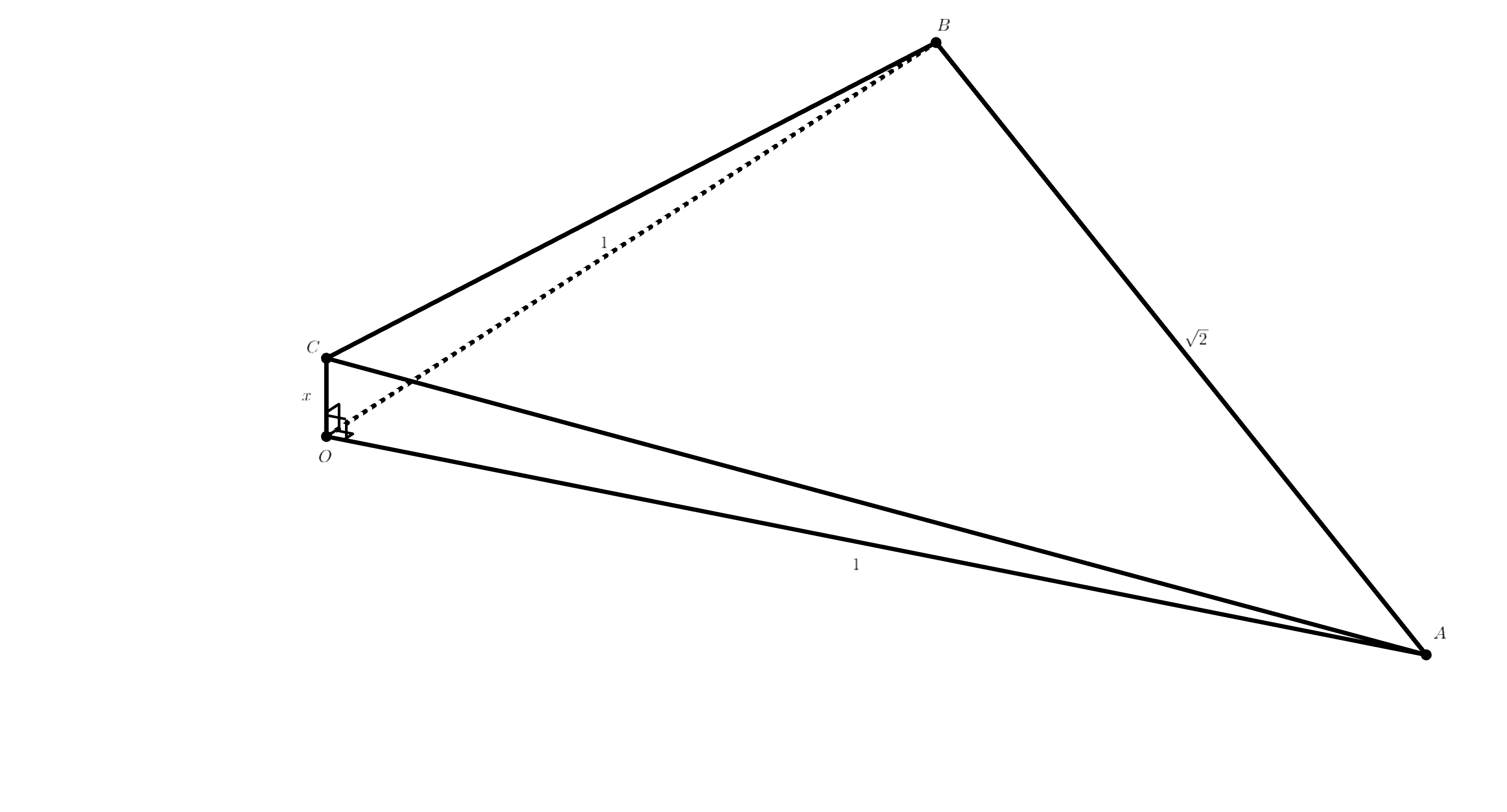
Рассмотрим три взаимно перпендикулярные прямые, пересекающиеся в точке Отложим на этих прямых от точки отрезки где — некоторый параметр (см. рис.). В тетраэдре есть три пары скрещивающихся перпендикулярных рёбер: ребро перпендикулярно плоскости следовательно, перпендикулярно ребру лежащему в этой плоскости; аналогично ребра и перпендикулярны ребрам и соответственно. Покажем, что можно подобрать параметр так, что сторона одного из построенных квадратных сечений будет в раз больше стороны другого. Рассмотрим пару перпендикулярных скрещивающихся ребер и длин и По доказанному утверждению длина стороны соответствующего квадратного сечения равна

Теперь возьмём пару перпендикулярных скрещивающихся рёбер и длины и Сторона соответствующего квадратного сечения будет равна

Рассмотрим функцию Она непрерывна при и Далее, поэтому

т.е. По теореме о промежуточном значении непрерывной функции на отрезке существует такое что Для найденного возьмём получившийся тетраэдр Искомый тетраэдр подобен с коэффициентом подобия

______________________________________________________________________________________________________________________________________________________

Второе решение.

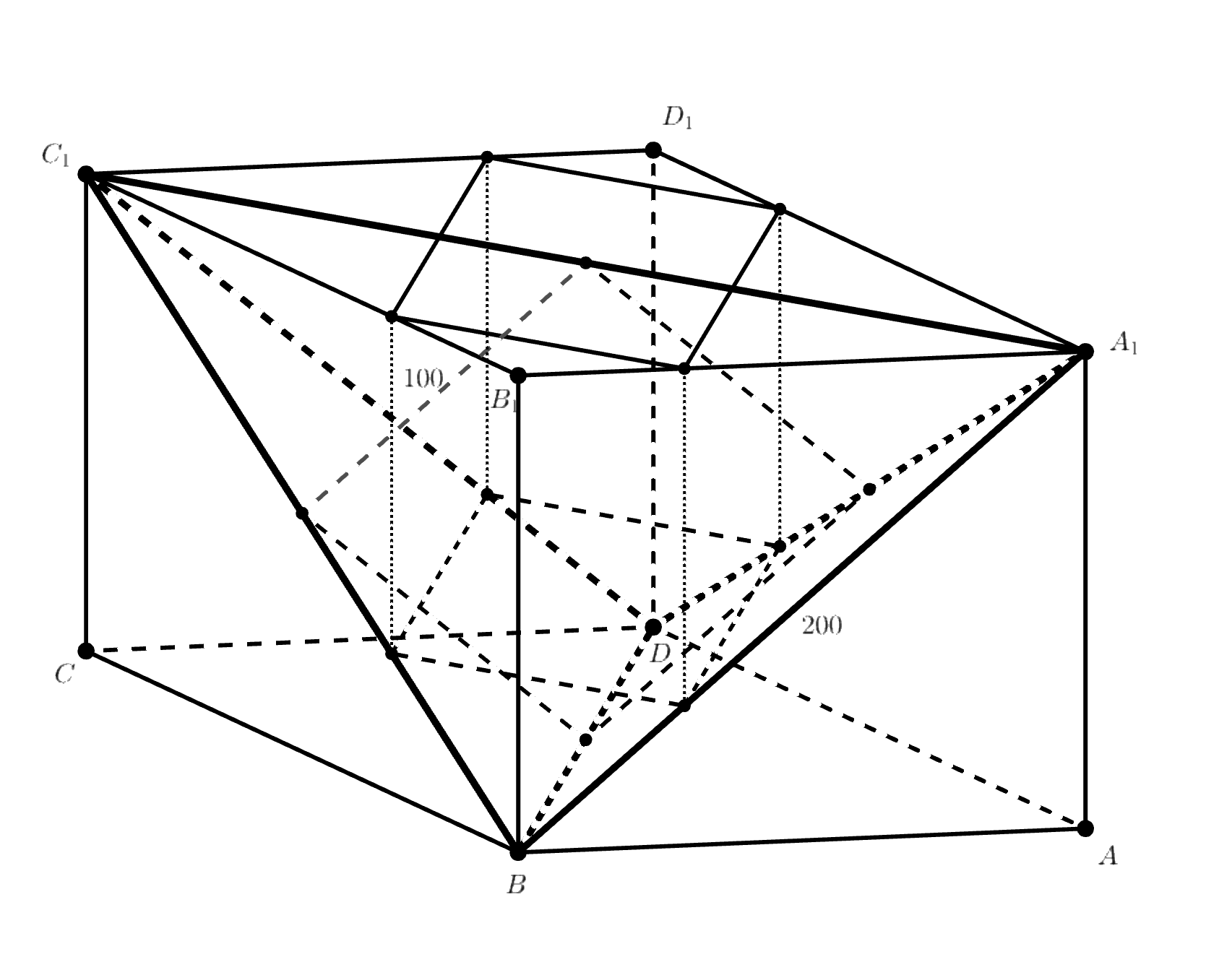
Рассмотрим параллелепипед боковые грани которого являются квадратами с диагоналями, равными а верхняя и нижняя грани — ромбы. Рассмотрим тетраэдр (см. рис.). Поскольку диагонали граней параллелепипеда перпендикулярны, а диагонали его противоположных граней попарно параллельны, пары скрещивающихся рёбер тетраэдра перпендикулярны. Согласно первому решению у такого тетраэдра есть три квадратных сечения, параллельных парам его скрещивающихся рёбер. Сторона квадратного сечения тетраэдра, параллельного рёбрам и будет равна

Покажем, что можно выбрать ромб в верхнем и нижнем основаниях параллелепипеда таким образом, что квадратное сечение тетраэдра, параллельное рёбрам и будет иметь сторону длины Спроектируем параллелепипед на верхнюю грань, при этом рёбра тетраэдра спроектируются на стороны ромба а квадрат сечения тетраэдра, параллельного прямым и спроектируется в равный ему квадрат, вершины которого будут лежать на сторонах ромба Сторона вписанного в ромб квадрата не превосходит меньшей диагонали ромба, поэтому, устремляя длину меньшей диагонали ромба к получим квадрат со стороной, сколь угодно близкой к нулю. В то же время, если в качестве ромба взять квадрат, то сторона вписанного квадрата будет равна В силу непрерывности изменения длины стороны вписанного квадрата найдётся такой ромб, что сторона вписанного в него квадрата равна что и требовалось.