Стереометрия на ММО

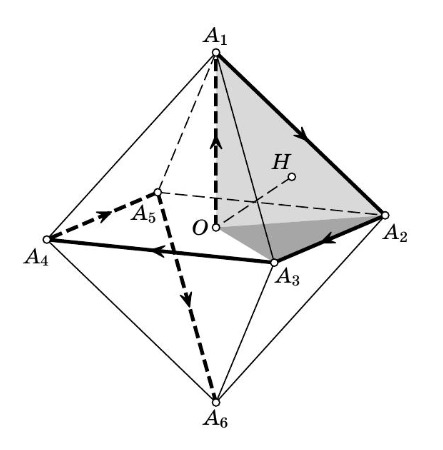
Пусть корабль находится в некоторой точке Рассмотрим правильный октаэдр описанный возле шара радиуса с центром в точке Докажем, что путь заведомо позволит достигнуть граничной плоскости.

Предположим противное. Тогда вершины октаэдра, а значит, и сам октаэдр (выпуклая оболочка его вершин) лежат строго внутри полупространства. Поэтому вписанный шар октаэдра, радиус которого равен тоже лежит строго внутри полупространства. Получаем противоречие, так как по условию расстояние до граничной плоскости полупространства равно

Покажем теперь, что длина пути меньше Пусть — высота пирамиды Запишем ее объём двумя способами:

Отсюда получаем, что а длина ребра октаэдра равна Поэтому длина пути равна так как