Планиметрия на Всесибе

Первое решение.

Величина угла равна . Если бы луч лежал бы вне угла величина угла равнялась бы сумме величин и и была бы больше градусов, что противоречит условию. Следовательно, луч лежит внутри угла поэтому величина угла равна сумме величин углов и то есть градусам. Значит, угол — прямой и треугольник является прямоугольным с гипотенузой AC , а точка O середина стороны AC.

Обозначим точку пересечения биссектрисы со стороной за Углы и равны следовательно, прямые и симметричны относительно биссектрисы то же самое верно и для прямых и Значит, треугольники и равны и точки и симметричны относительно а треугольник прямоугольный равнобедренный.

Продлим отрезок до пересечения со стороной в точке симметричной относительно биссектрисы Обозначим за середину отрезка по теореме обратной теореме Фалеса отрезки и параллельны, следовательно угол равен углу то есть градусам. Значит, треугольник — прямоугольный равнобедренный и равен треугольникам и Отсюда следует, что точки и делят отрезок на три одинаковых части.

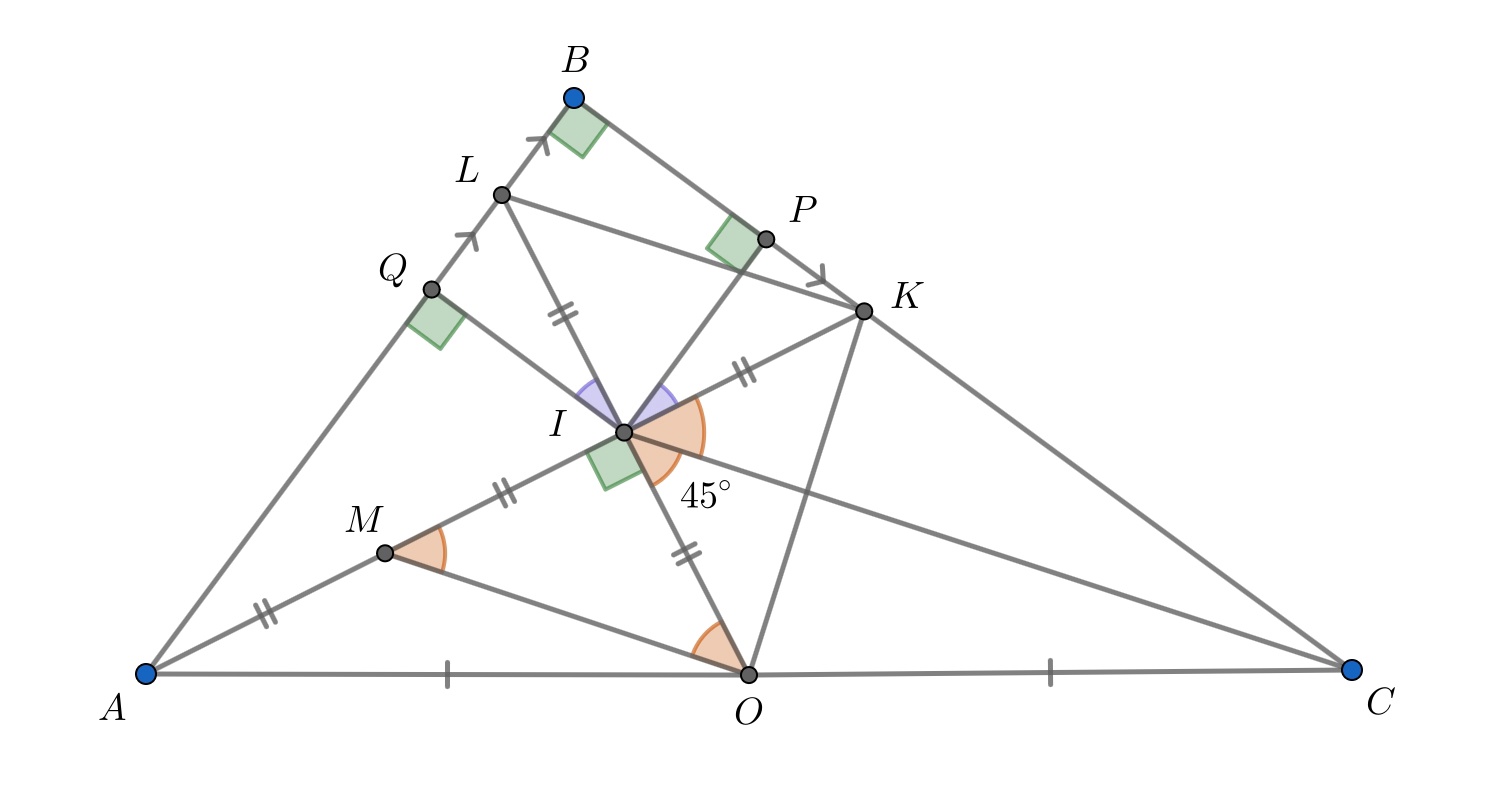
Опустим из точки перпендикуляры и на стороны и соответственно, точки и являются точками касания этих сторон со вписанной окружностью, четырёхугольник является квадратом. Углы и прямые, значит, углы и равны, отсюда следует равенство прямоугольных треугольников и По теореме Фалеса длина равна половине длины а длина вдвое больше длины

Следовательно, длина стороны равна Из теоремы Пифагора Следовательно,

______________________________________________________________________________________________________________________________________________________

Второе решение.

Пункт 1, точки те же, что как в первом решении, четырёхугольник является квадратом.

В прямоугольном треугольнике катет вдвое больше катета Считаем длину равной единице, тогда площадь треугольника равна длина гипотенузы АО равна , а высота из вершины равна . Эта высота и отрезки и равны, как радиусы вписанной окружности, поэтому

Следовательно,

Из теоремы Пифагора , откуда