Планиметрия на Всесибе
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
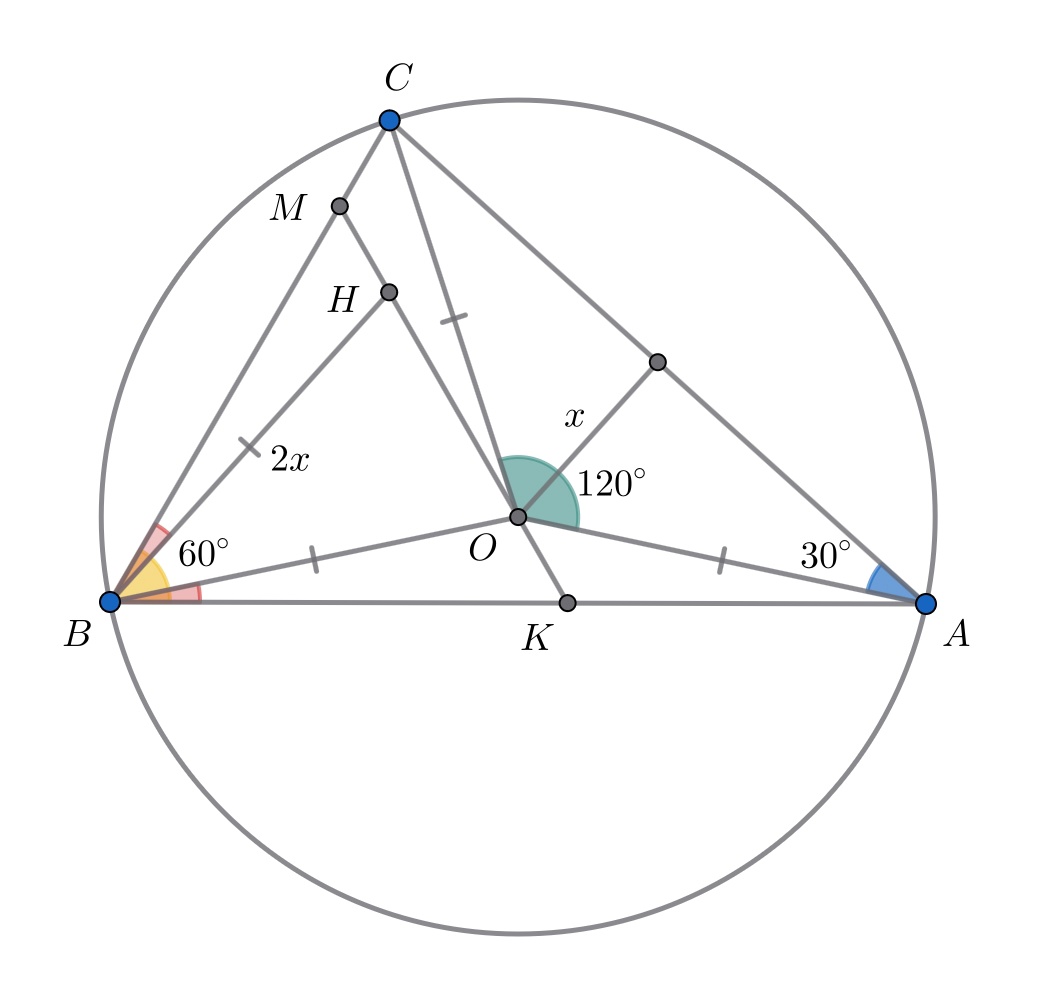
В остроугольном треугольнике 
с углом 
при вершине 
обозначим за 
центр описанной окружности, за 
— точку
пересечения высот. Прямая 
пересекает стороны 
и 
в точках 
и 
соответственно. Доказать, что треугольник 
—
равносторонний.
Источники:
Подсказка 1:
Попробуйте обозначить через R радиус описанной окружности треугольника, а углы через α, β, γ. Как отрезок BH выражается через эти параметры? А если учесть, что бета равно 60°?
Подсказка 2:
Итак, кажется, вы получили, что треугольник BHO равнобедренный. Было бы здорово, если бы его биссектриса из точки B оказалась биссектрисой и в KBM.
Подсказка 3:
Если на этом этапе возникли трудности, вспомните (или изучите) свойства ортоцентра, это поможет :)
Специальные программы
Программа
лояльности вер. 2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к твоему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас важно быть полезными учителям по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
RuStore
AppStore